流量网络
• 想要将一些水从S运到T，必须经过一些水站，链接水站的是管道，每条管道都有它的最大能容纳的水量，求最多S到T能流多少流量。

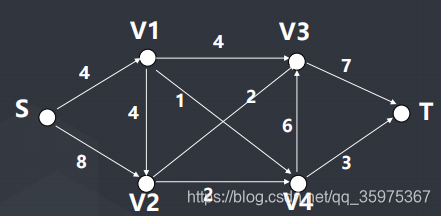
基本概念
• 这是一个典型的网络流模型。我们先了解网络流的有关定义和概念。
• 若有向图G=(V,E)满足下列条件：

1. 有且仅有一个顶点S，它的入度为零，即d-(S) = 0，这个顶点S便称为源点，或称为发点。
2. 有且仅有一个顶点T，它的出度为零，即d+(T) = 0，这个顶点T便称为汇点，或称为收点。
3. 每一条弧都有非负数，叫做该边的容量。边(vi, vj)的容量用cij表示。
   • 则称之为网络流图，记为G = (V, E, C)
   
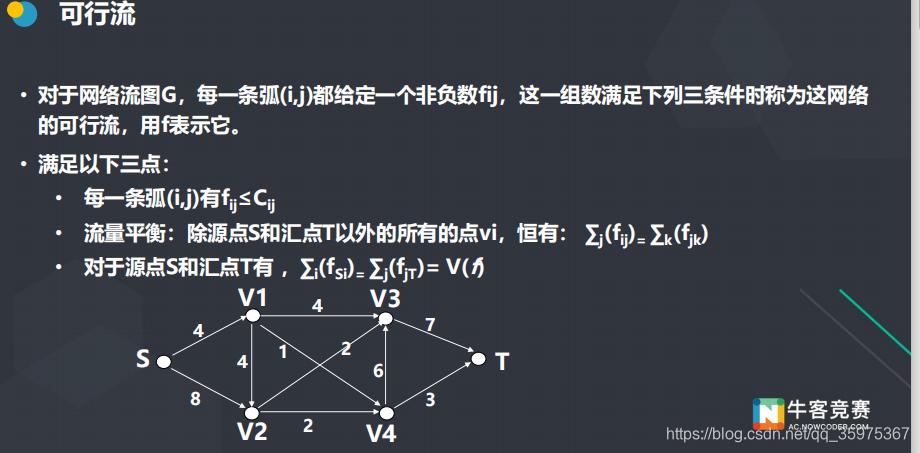
   1 .水流不递增
   2 .不能存水
   3 流入多少水流出多少水

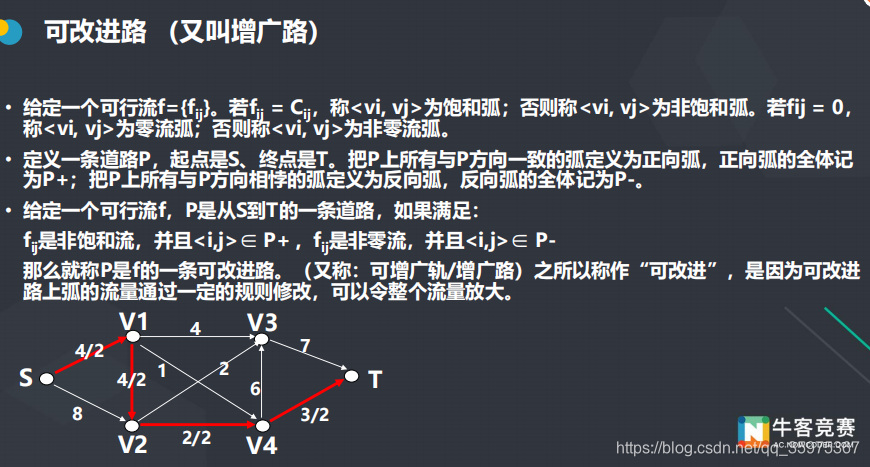
可改进路（增广路）

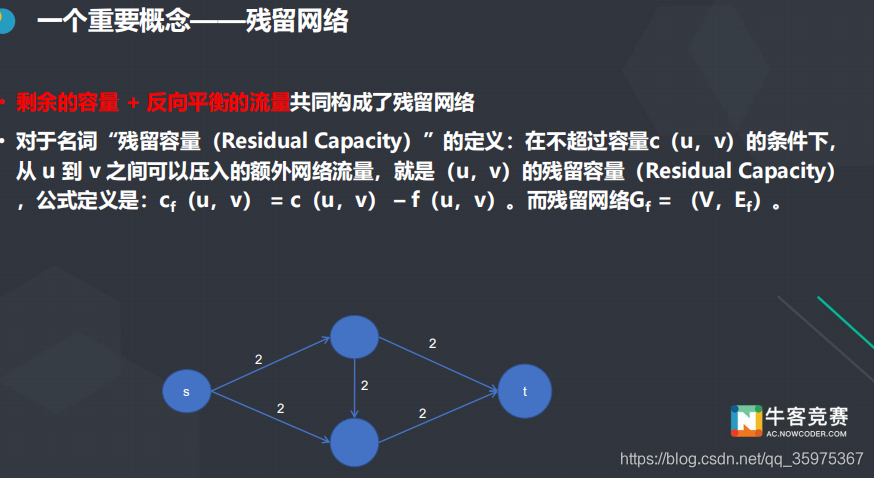
残留网络

割切

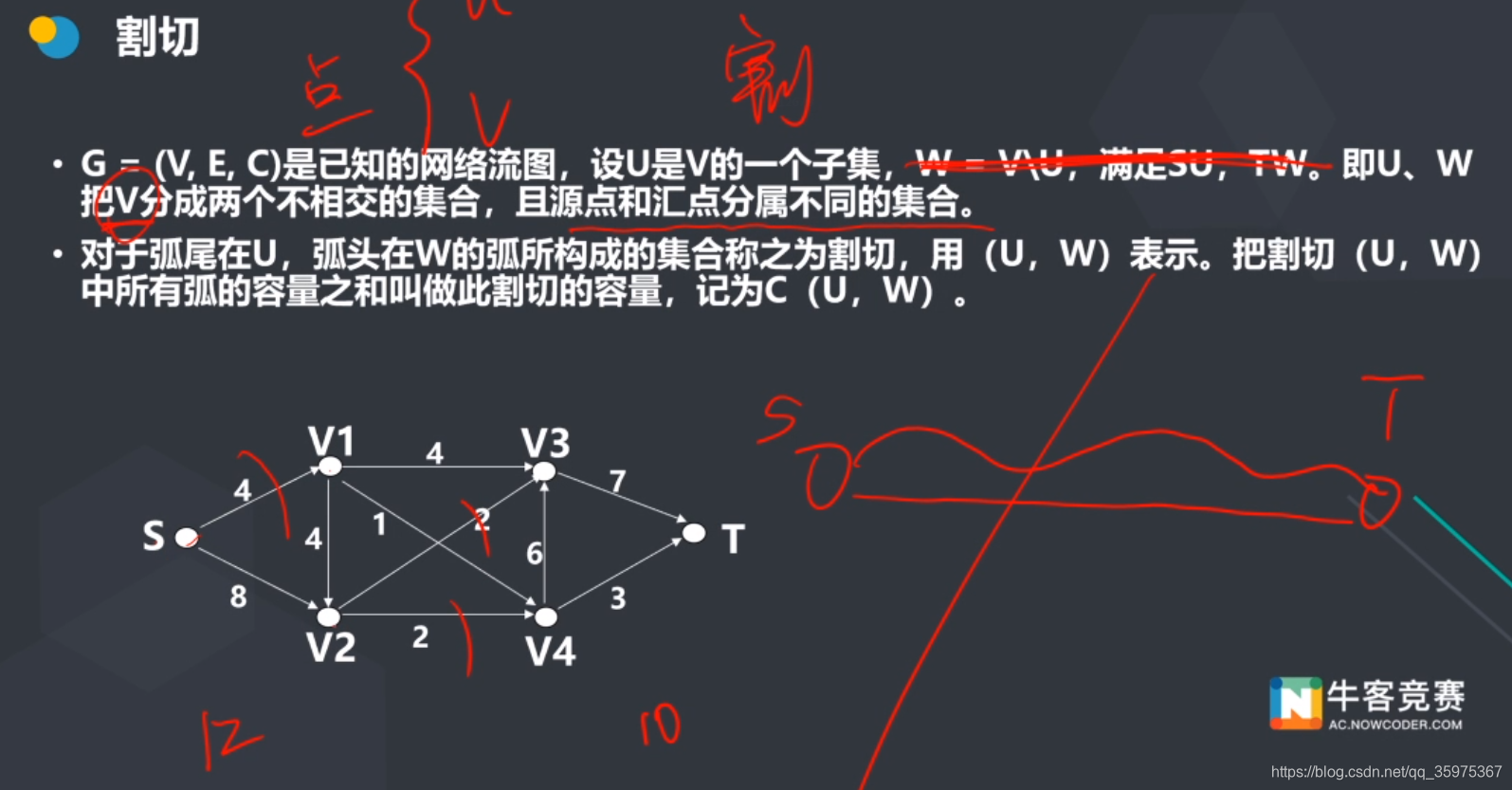
找一个方法，把S和T断开，所切截面为流量
所能通过的水流为截面，
所以最大流等于最小割

流量算法的基本理论

• 定理1：对于已知的网络流图，设任意一可行流为f，任意一割切为(U, W)，必有：V(f) ≤ C(U, W)。
• 定理2：可行流f是最大流的充分必要条件是：f的残量网络中不存在可改进路。
• 定理3：整流定理——
如果网络中所有的弧的容量是整数，则存在整数值的最大流。
• 定理4：最大流最小割定理——
最大流等于最小割，即max V(f) = min C(U, W)。

方法：

Ford-Fulkson方法
FF方法

Edmond-Karp算法

• EK算法是FF方法中最简单的一个，当然效率也就比较低
• EK算法的流程与ff方法完全相同，只是在寻找增广路的时候使用了BFS
• 时间复杂度O（n*m^2）
• 空间复杂度O（n^2）（邻接矩阵）
• 注意要退流哦！！！！
复杂度太高基本不用

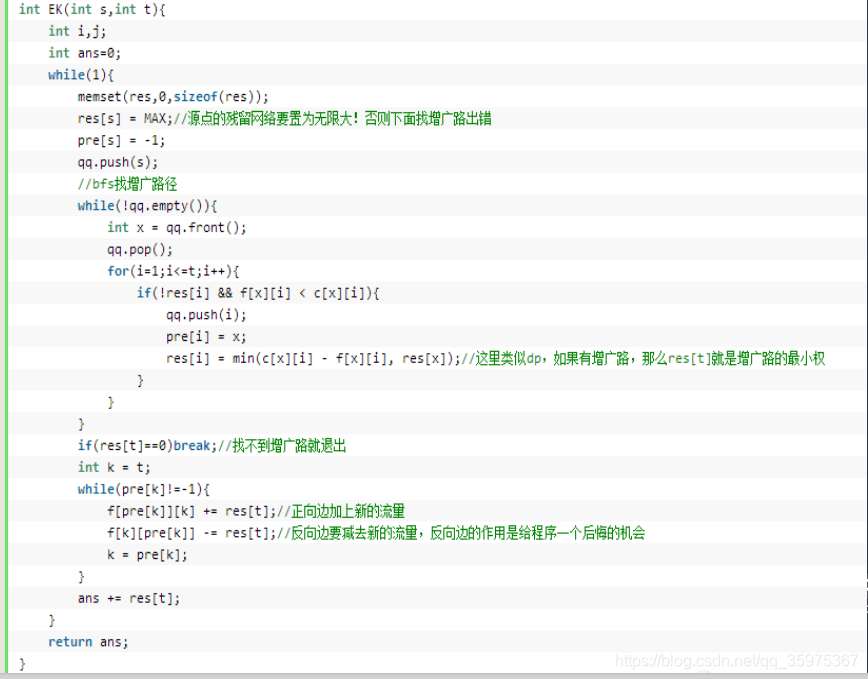
代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=205;
const int inf=0x7fffffff;
int r[maxn][maxn]; //残留网络，初始化为原图
bool visit[maxn];
int pre[maxn];
int m,n;
bool bfs(int s,int t)  //寻找一条从s到t的增广路，若找到返回true
{int p;queue<int > q;memset(pre,-1,sizeof(pre));memset(visit,false,sizeof(visit));pre[s]=s;visit[s]=true;q.push(s);while(!q.empty()){p=q.front();q.pop();for(int i=1;i<=n;i++){if(r[p][i]>0&&!visit[i]){pre[i]=p;visit[i]=true;if(i==t) return true;q.push(i);}}}return false;
}
int EdmondsKarp(int s,int t)
{int flow=0,d,i;while(bfs(s,t)){d=inf;for(i=t;i!=s;i=pre[i])d=d<r[pre[i]][i]? d:r[pre[i]][i];for(i=t;i!=s;i=pre[i]){r[pre[i]][i]-=d;r[i][pre[i]]+=d;}flow+=d;}return flow;
}int main()
{while(scanf("%d%d",&m,&n)!=EOF){int u,v,w;memset(r,0,sizeof(r));///for(int i=0;i<m;i++){scanf("%d%d%d",&u,&v,&w);r[u][v]+=w;}printf("%d\n",EdmondsKarp(1,n));}return 0;
}

Sap算法

• sap算法是采用了距离标号的方法求最短增广路， 而距离标号的思想来自于push__relable（压入重标记）类算法
• 有兴趣的同学可以去了解一下push__relable类算法

int dfs(int x,int flow)
{if(x==t)return flow;//如果是汇点，从x流到t的流量 int sum=0;//当前情况下x流出多少流量 for(int i=1;i<=m;i++) {if(g[x][i]&&(d[x]==d[i]+1))//g[x][i]：x可以流到i {int tmp=dfs(i,min(g[x][i],flow-sum));//受限于x到i的边和剩余流量 g[x][i]-=tmp; g[i][x]+=tmp;//反向边 sum+=tmp;//流出tmp流量 if(sum==flow)return sum;//如果所有流量用完了 //如果流量没有用完，继续循环 }}if(d[S]==-1)return sum;//出现断层，已经断开 cntd[d[x]]--;//cntd[i]第i层有多少点   d[x]层的点 if(!cntd[d[x]])//这层没点了 ，说明出现断层 d[S]=-1;    //S最多在第m-1层，当出现在第-1层说明为不合理情况，要退出 ，相当于退出标记 d[x]++;//上升一层 cntd[d[x]]++;//层数点加1 return sum;
}dfs(S,inf);

Dinic算法

• Dinic算法是一个基于“层次图”的时间效率优先的最大流算法。
• 层次图是什么东西呢？层次，其实就是从源点走到那个点的最短路径长度。
• 于是乎，我们得到一个定理：从源点开始，在层次图中沿着边不管怎么走，经过的路径一定
是终点在剩余图中的最短路。

• Dinic算法也有类似于sap的为顶点定标的过程——通常用BFS实现……
• 每次从源点开始遍历，如果一次bfs可以从源点到汇点整个网络都会变成一个层次网络
• 在一个分层网络中， 只有a[i] = = a[j] or a[i] = = a[j] -1时<i，j>才有边存在。
• 当且仅当a[i] == a[j] -1时，两点之间的边才被称为有用边，在接下来的寻找增广路的过程中只会走这样的有用边。
• 因此，dfs的时候只要遍历到汇点即可因为同一层和下一层都更新不了汇点了

bool makelevel(int s,int t)
{memset(d,0,sizeof(d));memset(q,0,sizeof(q));d[s]=1;//s的层级为1int l=0,r=0;q[r++]=s;while(l<r){int x=q[l++];if(x==t)return 1;//到汇点时退出for(int i=head[x];i;i=edge[i].next){if((d[edge[i].t]==0)&&(edge[i].w!=0))//容量为0的边不能走&&该点的层级未被标记{q[r++]=edge[i].t;d[edge[i].t]=d[x]+1;//层级加一}}}return false;
}
int dfs(int x,int flow,int t)//从s到x流了多少流量
{if(x==t)return flow;int sum=0;for(int i=head[x];i;i=edge[i].next){if((edge[i].w!=0)&&(d[edge[i].t]==d[x]+1))//满足层级要求{int tmp=dfs(edge[i].t,min(flow-sum,edge[i].w),t);edge[i].w-=tmp;edge[i^1].w+=tmp;sum+=tmp;if(sum==flow)return sum;}}return sum;
}
while(makelevel(1,m))
{ans+=dfs(1,INF,m);
}

完整代码：

#include <bits/stdc++.h>
using namespace std;
const long long inf=2005020600;
int n,m,s,t,u,v;
long long w,ans,dis[520010];
int tot=1,now[520010],head[520010]; struct node {int to,net;long long val;
} e[520010];inline void add(int u,int v,long long w) {e[++tot].to=v;e[tot].val=w;e[tot].net=head[u];head[u]=tot;e[++tot].to=u;e[tot].val=0;e[tot].net=head[v];head[v]=tot;
}inline int bfs() {  //在惨量网络中构造分层图 for(register int i=1;i<=n;i++) dis[i]=inf;queue<int> q;q.push(s);dis[s]=0;now[s]=head[s];while(!q.empty()) {int x=q.front();q.pop();for(register int i=head[x];i;i=e[i].net) {int v=e[i].to;if(e[i].val>0&&dis[v]==inf) {q.push(v);now[v]=head[v];dis[v]=dis[x]+1;if(v==t) return 1;}}}return 0;
}inline int dfs(int x,long long sum) {  //sum是整条增广路对最大流的贡献if(x==t) return sum;long long k,res=0;  //k是当前最小的剩余容量 for(register int i=now[x];i&&sum;i=e[i].net) {now[x]=i;  //当前弧优化 int v=e[i].to;if(e[i].val>0&&(dis[v]==dis[x]+1)) {k=dfs(v,min(sum,e[i].val));if(k==0) dis[v]=inf;  //剪枝，去掉增广完毕的点 e[i].val-=k;e[i^1].val+=k;res+=k;  //res表示经过该点的所有流量和（相当于流出的总量） sum-=k;  //sum表示经过该点的剩余流量 }}return res;
}int main() {scanf("%d%d%d%d",&n,&m,&s,&t);for(register int i=1;i<=m;i++) {scanf("%d%d%lld",&u,&v,&w);add(u,v,w);}while(bfs()) {ans+=dfs(s,inf);  //流量守恒（流入=流出） }printf("%lld",ans);return 0;
}
//dinic时间复杂度:O(n^2 m).

最小费用最大流

• 带有费用的网络流图： G=（V，E，C，W） V：顶点； E：弧；C：弧的容量；W：单位流量费用。
在保证s到t流量最大的前提下，所需的费用最小，这就是最小费用最大流问题．

基本思路：

把弧<i,j>的单位费用w[i,j]看作弧<i,j>的路径长度，每次找从源点s到汇点t长度最短（费用最小）的可增广路径进行增广。

1. 最小费用可增广路
2. 路径s到t的长度即单位流量的费用。
   • 其实就是把ek算法中的广搜改成spfa……（因为存在负权边所以得用spfa）

代码：

bool spfa(int s,int t)
{queue<int>q;for(int i=0;i<N;i++){dis[i]=INF;vis[i]=0;pre[i]=-1;}dis[s]=0;vis[s]=1;q.push(s);while(!q.empty()){int u=q.front();q.pop();vis[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].to;if(edge[i].cap>edge[i].flow&&dis[v]>dis[u]+edge[i].cost){dis[v]=dis[u]+edge[i].cost;pre[v]=i;if(!vis[v]){vis[v]=1;q.push(v);}}}}if(pre[t]==-1)return 0;return 1;
}
int minCostMaxflow(int s,int t,int &cost)
{int flow=0;cost=0;while(spfa(s,t)){int Min=INF;for(int i=pre[t];i;i=pre[edge[i^1].to]){if(Min>edge[i].cap-edge[i].flow)Min=edge[i].cap-edge[i].flow;}for(int i=pre[t];i;i=pre[edge[i^1].to]){edge[i].flow+=Min;edge[i^1].flow-=Min;cost+=edge[i].cost;edge[i^1].flow+=edge[i].cost;edge[i].cost-=edge[i].cost;}flow+=Min;}return flow;
}
//返回的最大流，cost存的是最小费用 

洛谷模板题

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define ll long long
#define inf 50000000
#define re register
using namespace std;
struct po
{int from,to,dis,nxt,w;
}edge[250001];
int head[250001],cur[1000001],dep[60001],n,m,s,t,u,num=-1,x,y,l,tot,sum,k,fa[10001];
int dis[5001],vis[5001],xb[5001],flow[5001];
inline int read()
{int x=0,c=1;char ch=' ';while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();while(ch=='-')c*=-1,ch=getchar();while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();return x*c;
}
inline void add_edge(int from,int to,int w,int dis)
{edge[++num].nxt=head[from];edge[num].from=from;edge[num].to=to;edge[num].w=w;edge[num].dis=dis;head[from]=num;
}
inline void add(int from,int to,int w,int dis)
{add_edge(from,to,w,dis);add_edge(to,from,0,-dis);
}
inline bool spfa()
{memset(dis,100,sizeof(dis));memset(vis,0,sizeof(vis));queue<int> q;while(!q.empty())q.pop();for(re int i=1;i<=n;i++){fa[i]=-1;}vis[s]=1;dis[s]=0;fa[s]=0;flow[s]=inf;q.push(s);while(!q.empty()){int u=q.front();q.pop();vis[u]=0;for(re int i=head[u];i!=-1;i=edge[i].nxt){int v=edge[i].to;if(edge[i].w>0&&dis[v]>dis[u]+edge[i].dis){dis[v]=dis[u]+edge[i].dis;fa[v]=u;xb[v]=i;flow[v]=min(flow[u],edge[i].w);if(!vis[v]){vis[v]=1,q.push(v);}}}}return dis[t]<inf;
}
inline void max_flow()
{while(spfa()){int k=t;while(k!=s){edge[xb[k]].w-=flow[t];edge[xb[k]^1].w+=flow[t];k=fa[k];}tot+=flow[t];sum+=flow[t]*dis[t];}
}
int main()
{memset(head,-1,sizeof(head));int d;n=read();m=read();s=read();t=read();for(re int i=1;i<=m;i++){x=read();y=read();l=read();d=read();add(x,y,l,d);}max_flow();cout<<tot<<" "<<sum;
}