一、简介

 

eShopOnContainers是一个简化版的基于.NET Core和Docker等技术开发的面向微服务架构的参考应用。

该参考应用是一个简化版的在线商城/电子商务微服务参考示例应用。

其包含基于浏览器的Web应用、基于Xamarin的Android、IOS、Windows/UWP 移动应用，以及服务端应用。其中服务端包含多个自治微服务（每个都拥有自己的数据/ db），并且每个微服务都有不同的实现形式（简单的CRUD与DDD / CQRS模式）。使用Http作为客户端应用程序之间的通信协议。支持异步通信，使用Integration Events(集成事件)和Event Bus(事件总线)进行数据更新传播。

其中包含的服务：

1. Identity Micsroservice（身份微服务）：身份认证和授权。SQL Server

2. Catalog microservice（产品目录微服务）：产品资料的维护。SQL Server

3. Ordering microservice（订单微服务）：订单逻辑的处理。SQL Server

4. Basket microservice（购物车微服务）：购物车逻辑的处理。Redis

5. Marketing microservice（市场营销微服务）：市场营销逻辑的处理。MongoDB/CosmosDB 和SQL Serve

6. Locations microservice （位置微服务）：提供位置服务。MongoDB/CosmosDB 数据库。

7. [New] Payment microservice （支付微服务）：处理支付逻辑。

二、技术储备

1. 语言：.net Core、C#

2. 平台：Docker、Xamarin、K8S

3. 组件：RabbitMQ、IdentityServer4、Polly、Redis、MongoDb、Api Gateway、MsSqlServer

4. 模式：EventBus、CQRS、CAP

5. 管理：CI/CD

三、整体架构

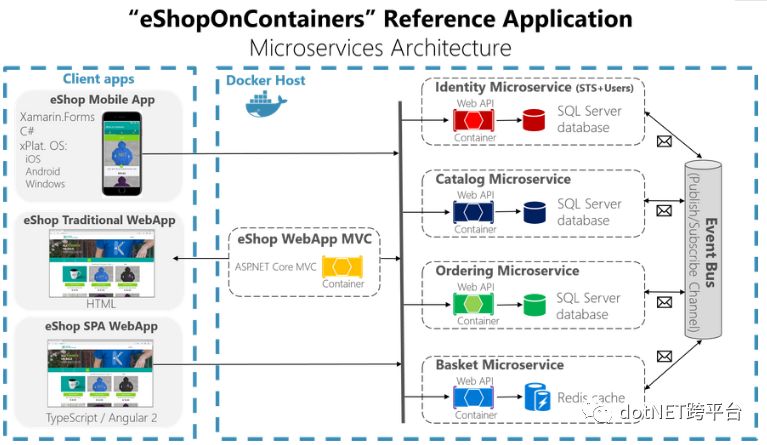
该架构主要包括两个部分：客户端应用和Docker主机中运行的服务端应用。

1. 客户端应用：基于浏览器的Web应用；基于Xamarin开发的Android、IOS、UWP移动应用。

2. 服务端应用：部署在在Doker主机的系列微服务。

四、服务架构

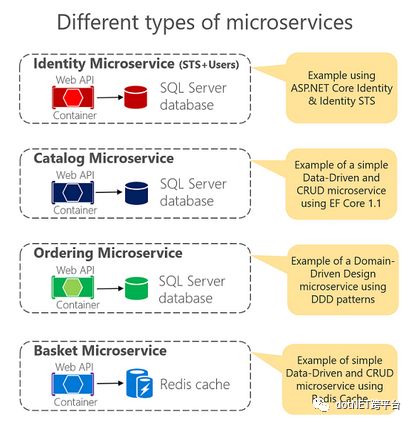
以上是微软展示的四种services，你还可以使用不同的框架，不同的数据库完成你的微服务搭建，这就是微服务为何如此流行的原因了。我可以利用任何语言，任何数据库都能搭建我的服务，无论我的调用端使用的何种语言，何种系统。

主要有两种架构模式

1. 基于数据驱动的CURD微服务

2. 基于DDD的微服务

而实际上，软件架构师和开发人员会使用不同的架构模式，比如（混合架构风格和架构模式）：

1. 简单的 CRUD，单层

2. 传统N层

3. DDD N层

4. 整洁架构

5. 命令和查询分离（CQRS）

6. 事件驱动架构

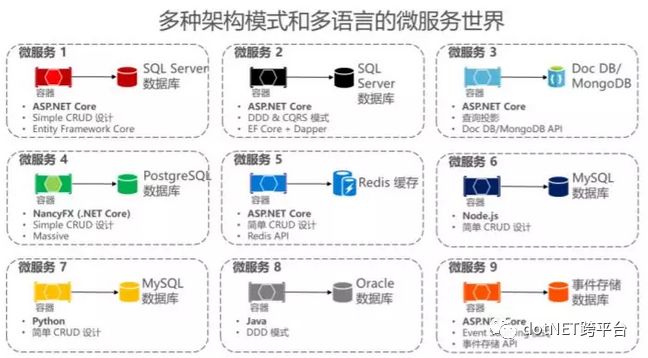
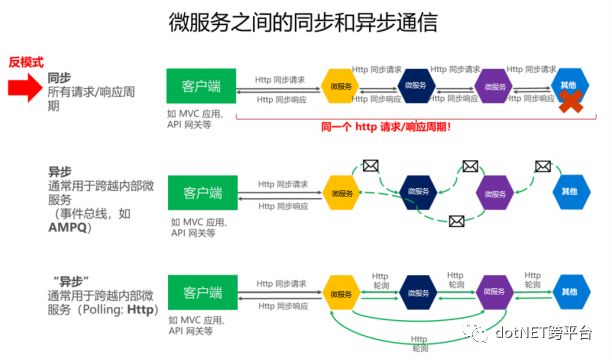
四、通信架构：

1. 客户端与微服务通过API网关通信：用于查询和接收来自客户端应用程序的更新或事务命令。

2. 异步事件通信：通过事件总线传播来自微服务的更新或与外部应用程序集成。事件总线可使用任何消息代理架构技术如 RabbitMQ来实现。