基本概念

点：平面上一点，用坐标(x,y)来表示

struct Point{double x,y;
}; 

向量：同时具有大小和方向的量 。把向量从原点出发到达的点的坐标作为该向量的坐标

typedef Point Vector;

点与向量的运算

点 + 向量 = 点
向量 + 向量 = 向量
点 - 点 = 向量
向量 * k = 向量

Vector operator +(Vector a,Vector b)
{return Vector(a.x+b.x,a.y+b.y);
}
Vector operator -(Vector a,Vector b)
{return Vector(a.x-b.x,a.y-b.y);
}
Vector operator *(Vector a,double p)
{return Vector(a.x*p , a.y*p);
}
Vector operator /(Vector a,double p)
{return Vector(a.x/p , a.y/p);
}

struct point{double x,y;point(){}point(double x1,double y1):x(x1),y(y1){}point operator +(const point &z)const{return point(x+z.x,y+z.y);}point operator -(const point &z)const{return point(x-z.x,y-z.y);}point operator 8 (const double &rate)const{return point(x*rate,y*rate);}
}p[N];

精度问题

因为浮点数的精度问题会造成微小的偏差

const double eps=1e-10;
int dcmp(double x)
{if(fabs(x)<eps)return 0;else return x>0?1;-1;
}
bool operator == (Point a,Point b)
{return !dcmp(a.x-b.x)&&!dcmp(a.y-b.y);
}

线段，射线和直线

表示方式：

1. 解析几何（y = kx+b）
2. 点+向量
3. 具体区分线段射线和直线

struct Line{Point p;Vector v;int f;
};
f=0 说明是线段
f=1 说明是射线 
f=2 说明是直线 

struct Line{point p,v;Line(){}Line(point _p.point _v):p(_p),v(_v){}
}L[N];

点积：

点积表示的是两个向量的长度之积再乘上他们夹角的余弦值，也就是a在b上的投影长度乘上b的模长

double dot(Vector a,Vector b)
{return a.x*b.x+a.y*b.y;
}

夹角

利用点积的定义：

double angle(Vector a,Vector b)
{return acos(dot(a,b)/length(a)/length(b));
}

叉积

叉积表示的是两个向量的长度之积再乘上它们的夹角的正弦值
也就是以这两个向量为相邻两边所成平行四边形的面积
（叉积还可以表示方向）

double cross(Vector a,Vector b)
{return a.x*b.y-a.y* b.x;
}

v2在v1的顺时针方向那么sin<v1,v2>就是负值，否则就输正值。“顺负逆正”
sin函数的符号就是叉积的符号
叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系：
若 P × Q > 0 , 则P在Q的顺时针方向。（用手势判断，大拇指朝上）
若 P × Q < 0 , 则P在Q的逆时针方向。
若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向。
a×b的方向：四指由a开始，指向b，拇指的指向就是a×b的方向，垂直于a和b所在的平面；（大拇指朝上为正）

向量的极角

求α
tan α=y/x
这里的极角范围是[-π， π)

double Polar_angle(int x,int y)
{return atan2(y,x);
}

旋转一个向量

利用极坐标

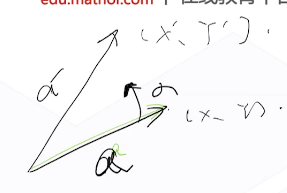
point rotate(double alpha)
{return point(x * cos(alpha) - y * sin(alpha),x * sim(alpha) + y * cos(alpha));
}

求三角形面积

此处为有向面积

double trianglearea(Point a,Point b,Point c)
{return cross(b-a,c-a)/2;
}

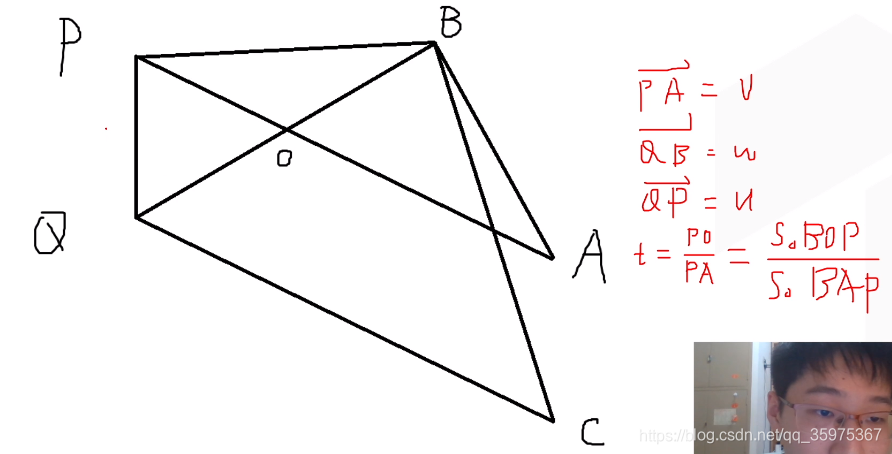
直线交点

Point getline(Point p,Vector v,Point q,Vector w)
{Vector u=p-q;double t=cross(w,u)/cross(v,w);return p+v*t;
}

有正负性质

点到直线距离

double distancetoline(Point p,point a,Point b)
{Vector v1=b-a,v2=p-a;return fabs(cross(v1,v2))/length(v1);
}

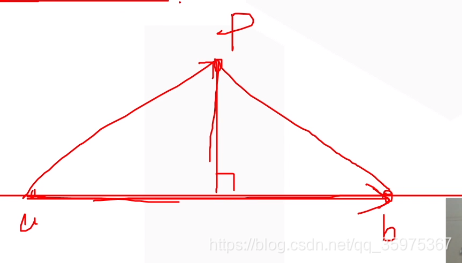
点在直线上的投影

double getlineprojection(Point p,Point a,Point b)
{Vector v=b-a;return a+v*(dot(v,p-a)/dot(v,v));
}

dot(v,v):ab的模长
dot(v,p-a):ab的模长 * ap的模长

判断两条线段是否相交

bool segement(Point a1,Point a2,Point b1,Point b2)
{double c1=cross(a2-a1,b1-a1);double c2=cross(a2-a1,b2-b1);double c3=cross(b2-b1,a1-b1);double c4=cross(b2-b1,a2-b1);return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}

返回是否等号
相当于判断b1和b2是否在线段a1a2的两侧

点与直线的位置关系

点是否在直线左侧

利用叉积的性质

bool onleft(Line l,Point p)
{return cross(l.v,p-l.p)>0;
}

点p是否在直线l的左侧
大于 0说明点在线段的左侧

点是否在直线上

bool on_line(Line l,Point p)
{return fabs(cross(l.v,p-l.p))<eps;
}

点是否在线段上

bool on_seg(Point a,Point b,Point p)
{bool flag1=fabs((p-a),(b-a))<eps;//AB与PA的叉积=0 bool flag2=dot(p-a,p-b)<-eps;//PA与PB的点积<0 return flag1&flag2;
}

点与多边形的位置关系

判断点与多边形的内部，外部或者边上（不一定为凸多边形）
判断点在边哪一侧（适用于凸多边形）

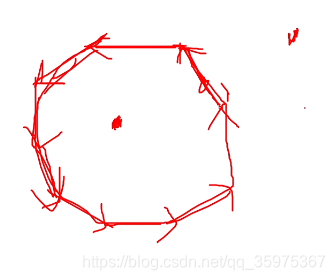
扫描法：

从给定点水平向右放出射线，根据射线与多边形交点个数的奇偶性来判断
考虑特殊情况：射线与顶点相交或与边重合
解决方法：水平边不考虑，顶点只考虑在对应边上较高或较低的点

转角法

求出从一固定点沿某一方向每次连接多边形上相邻两点所成有向角之和
若该点在多边形内，角度和为360度，在多边形外则为0度

利用叉积来求角度（带方向）

线段与多边形位置关系

先判断线段的两个端点
若线段与某条边严格相交，则必然不在多边形内

若线段与若干顶点相交，则需要考虑相邻交点连成的线段是否在多边形内

多边形的面积

与转角法类似，只需要每次所形成的三角形的有向面积累加即可

double area(Vector<Point>poly)
{double sum=cross(poly[0],poly[poly.size()-1]);for(int i=1;i<poly.size();i++)sum+=cross(poly[i],poly[i-1]);return sum/2;
}