一、什么是docker

Docker 是一个开源项目，通过把应用程序打包为可移植的、自给自足的容器（可以运行在云端或本地）的方式，实现应用程序的自动化部署。

使用 Docker 的时候，需要创建一个应用或服务，然后把它和它的依赖打包到一个容器镜像中。镜像是应用或服务，以及它的配置和依赖的静态表现形式。要运行应用和服务，这个应用的镜像会被实例化，来创建一个容器，这个容器将会运行在 Docker 宿主机上。Docker公司 维护了一个公用的注册表叫 Docker Hub，其他提供商也为不同的镜像集合提供了各种注册表。此外，企业可以在本地创建一个私有的 注册表，供企业内部的 Docker 镜像来使用。 

这里出现几个名词。

容器镜像：一个包含了创建容器所需的所有依赖和信息的“包”。

容器：Docker 镜像的一个实例。

注册表（Registry）：为仓库提供访问服务。一个注册表通常包含来自于多个团队的仓库。企业通常会创建私有的 注册表来存储和管理他们创建的镜像。

Docker Hub：一个公用的 注册表。

 

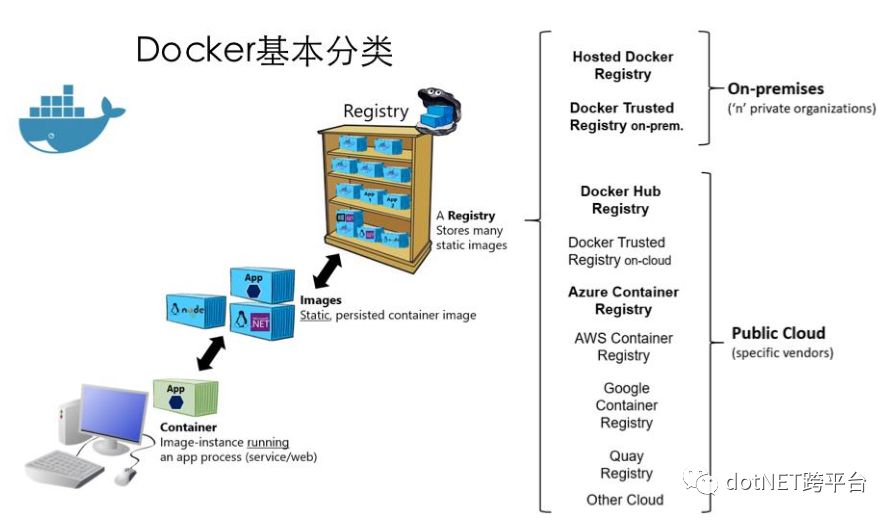
需要注意：Windows 镜像只能运行在Windows 主机上，Linux 镜像只能运行在 Linux 主机上。 

 

二、环境设置

安装docker我们就不说了，网上很多介绍。我们从配置开始

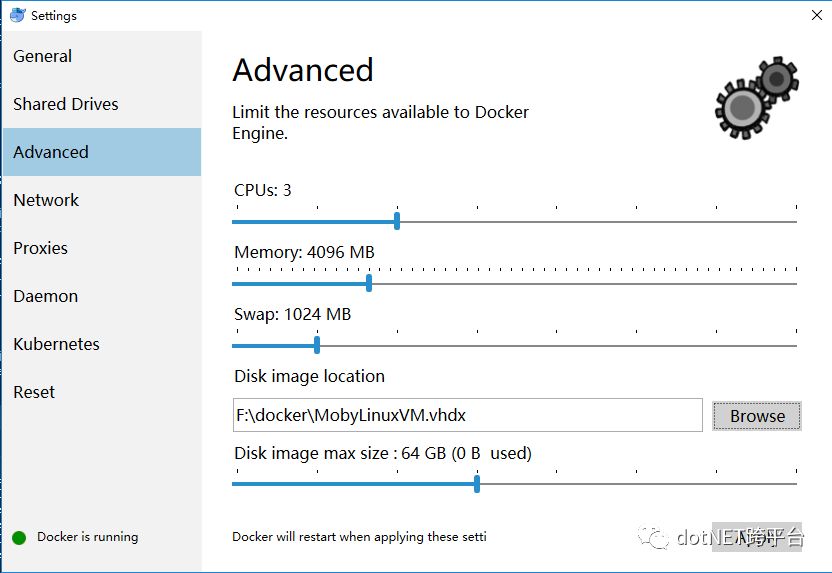
1、 给Docker分配CPU和内存

对硬件还是有些要求的。

 

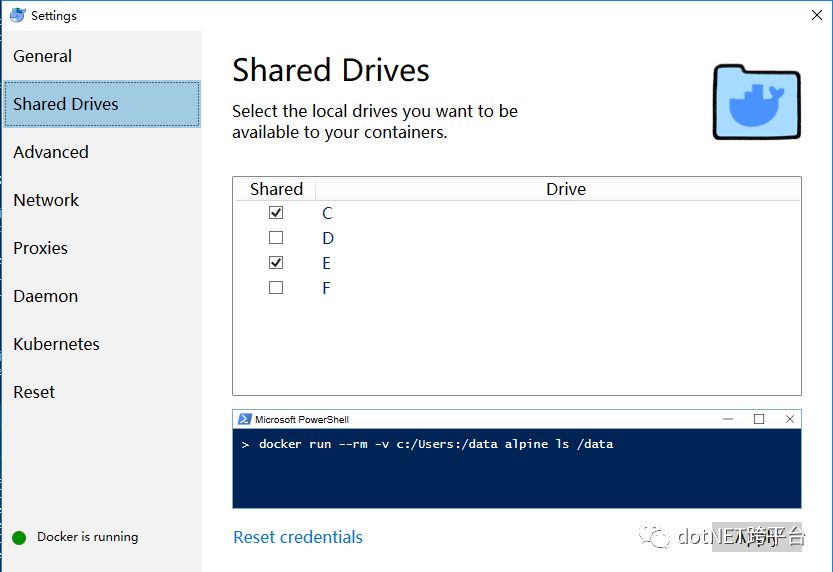
 2 、设置共享驱动器

这里C盘是必须的，另外E盘是我存放eshop源代码的盘，自然也要共享。

3、设置镜像加速

我们使用DaoCloud来做镜像加速。官网https://www.daocloud.io

加速地址 http://f1361db2.m.daocloud.io加到"registry-mirrors"的数组里，点击 Apply 。

 

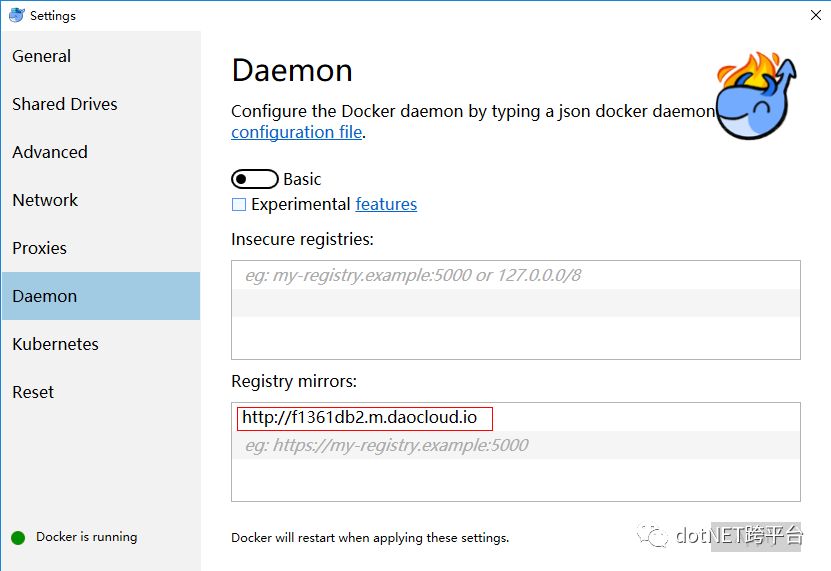
4、防火墙设置

　　在本地防火墙中打开端口，以便可以通过STS（安全令牌服务容器，IP：10.0.75.1 ）进行身份验证，该IP为Docker默认设置。Xamarin app或SPA app等客户端也需要打开相应的防火墙端口。

　　您可以在本地防火墙中手动创建规则，也可以通过执行解决方案的cli-windows目录中提供的add-firewall-rules-for-sts-auth-thru-docker.ps1脚本来创建该规则。
　　您需要通过在防火墙中创建一个IN-BOUND RULE来打开解决方案使用的端口5100到5110，如下面的屏幕截图所示（对于Windows）。

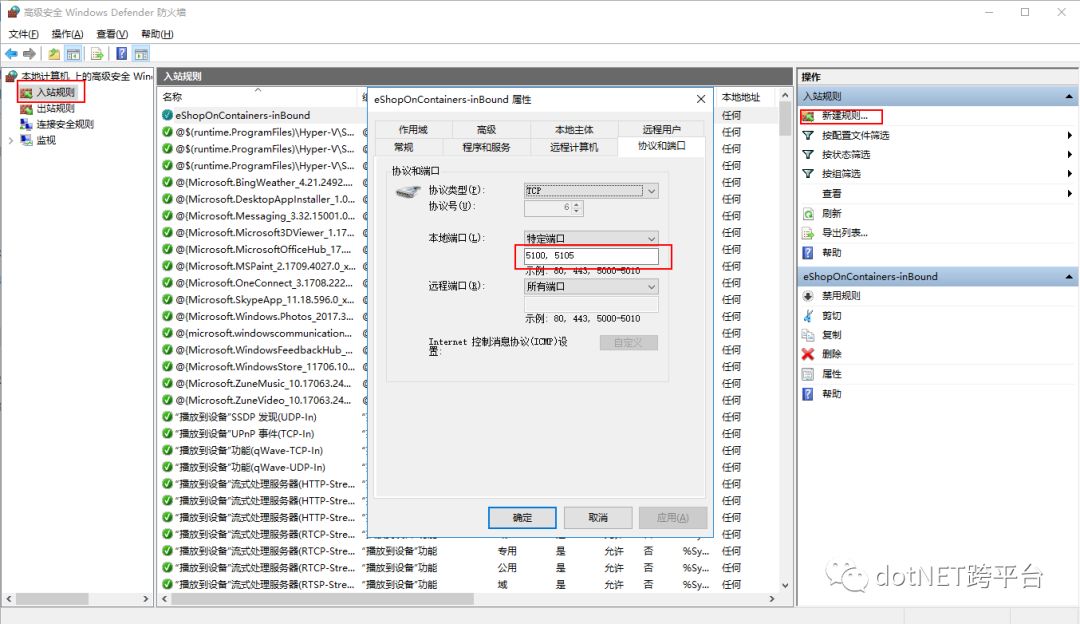
　　注意：通过PowerShell脚本设置防火墙规则时可能会因为Windows PowerShell® 默认执行策略未设置而报错。具体参考：https://go.microsoft.com/fwlink/?LinkID=135170。　　可以通过PowerShell执行"Set-ExecutionPolicy UNRESTRICTED -Scope CurrentUser"命令临时允许脚本运行，运行完设置防火墙规则脚本后再通过“Set-ExecutionPolicy Undefined -Scope CurrentUser”还原默认设置。要查看当前执行策略设置可通过命令：“ Get-ExecutionPolicy -List”。

三、构建并部署到本机Docker主机

1、打开并运行eShopOnContainers解决方案

　　如果只进行服务端调试，打开“eShopOnContainers-ServicesAndWebApps.sln”解决方案，如果还需要调试移动App，打开“eShopOnContainers.sln”解决方案。

　　将“docker-compose”设置为默认启动项目，按F5或者点运行。

　　注意：由于第一次运行Docker需从互联网下载"SQL for Linux , Redis , ASPNET"等Docker镜像，视网速可能需要等10分钟左右。

2、查看已经构建好的镜像。

 

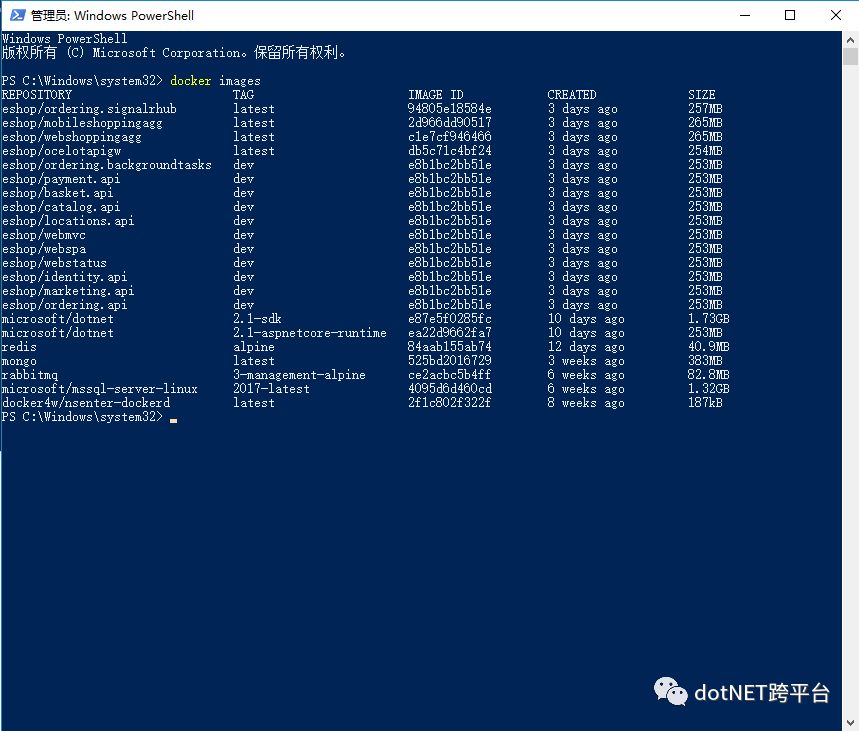
注：你可能会看到很多为 <none>的镜像，这些是临时镜像，可以通过命令 docker rmi $(docker images-f"dangling=true"-q)删除。

3、测试所有应用程序和微服务

完成容器部署，测试访问以下服务。 

容器正常部署运行后，可通过以下地址访问任一应用或服务:

• MVC网页: http://localhost:5100

• 单页应用网页: http://localhost:5104 (需要单独安装依赖并编译才能正常运行)

• 商品目录微服务: http://localhost:5101 (不需要认证)

• 订单微服务: http://localhost:5102 (需要认证)

• 购物车微服务: http://localhost:5103 (需要认证)

• 认证微服务: http://localhost:5105

• 订单数据库(SQL Server 连接字符串): Server=tcp:localhost,5432;Database=Microsoft.eShopOnContainers.Services.OrderingDb;User Id=sa;Password=Pass@word;

• 商品目录数据库 (SQL Server 连接字符串): Server=tcp:localhost,5434;Database=CatalogDB;User Id=sa;Password=Pass@word

• 认证数据库 (SQL Server 连接字符串): Server=localhost,5433;Database=aspnet-Microsoft.eShopOnContainers;User Id=sa;Password=Pass@word

• 购物车数据 (Redis): 监听 localhost:6379

相关文章：

• eShopOnContainers 看微服务 ①：总体概览

• eShopOnContainers 知多少[1]：总体概览

• eShopOnContainers 知多少[2]：Run起来
  

• eShopOnContainers 知多少[3]：Identity Microservice

• eShopOnContainers 知多少[4]：Catalog microservice

• Catalog Service - 解析微软微服务架构eShopOnContainers（三）
  

• eShopOnContainers 知多少[5]：EventBus With RabbitMQ

• EventBus In eShop -- 解析微软微服务架构eShopOnContainers（四）
  

• eShopOnContainers 是一个基于微服务的.NET Core示例框架

原文地址：https://www.cnblogs.com/tianyamoon/p/10081277.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com