直线：

struct Line{point p,v;Line(){}Line(point _p.point _v):p(_p),v(_v){}
}L[N];

图形：

求垂足

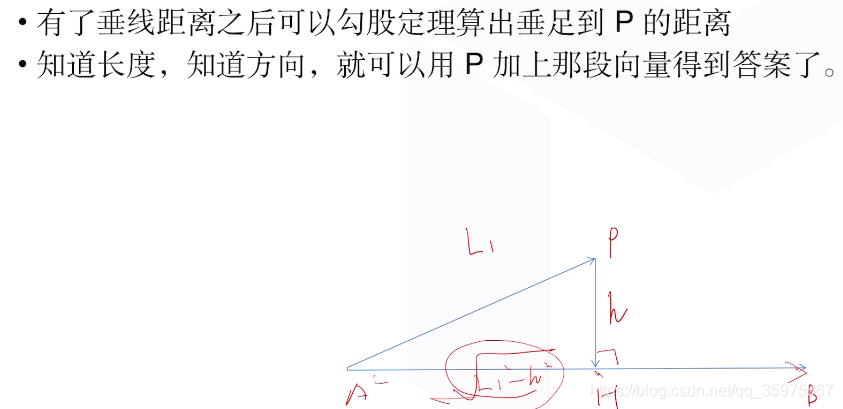
point vp(Line l,point p)//求p点向l做垂线得到的垂足 
{double Dis=dis(l,p);//求p到l的距离Dis Dis=Dis*Dis;double pDis=(p-l.p).length();//求AP距离pDis pDis=pDis*pDis;double vDis=sqrt(pDis-Dis);//勾股定理得到AH距离 point ans=l.p+l.v*(vDis/l.v.length());//通过方向单位向量乘长度得到路径，加起点得到答案 return ans;
}

求两圆交点

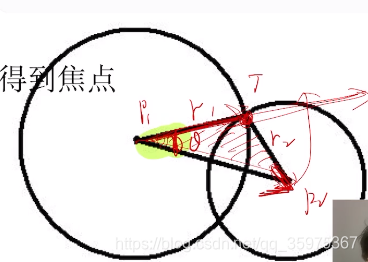
1. 先求余弦定理 cosp1
2. 反函数 角p1
3. p1p2旋转到p11T方向
4. 调整长度
5. p1+p1T向量=T
   代码：

point get_intersection(circle A,circle B)
{point AB=B.o-A.o;double costheta=AB.length() * AB.length() + A.r *A.r-B.r*B.r;costheta=costheta/(2*AB.length()*A.r);//余弦定理AB=AB.rotatr(acos(costheta));//旋转theta角return A.o+AB*(A.r/AB.length()); 
} 

直线与圆交点

代码：

point get_intersection(circle A,Line B)
{point H=vp(B,A.o);//求垂线 double OH=(H-A.o).length();double HY=sqrt(A.r * A.r -OH * OH);return H + B.v *(HY/B.v.length());// return H + B.v *(-HY/B.v.length());
}

点+单位向量 * 长度

多边形问题

平面上n个点收尾顺次连接组成的平面图形
可能是凸多边形或者凹多边形

判断一个点是否在任意多边形内部

从这个点出发引一条射线，如果这个射线与多边形有奇数个交点则在内部，否则在外部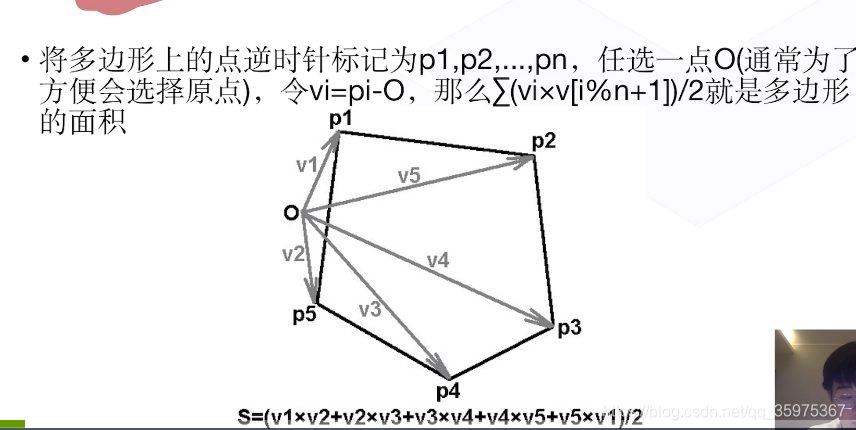

double calc_S()
{double ans=0;int n=poly.size();for(int i=1;i<n;i++)ans+=poly[i-1]^poly[i];ans+=poly[n-1]^poly[0];return ans/2;
}

Pick定理

对于顶点都是整点的多边形，设其面积为S，多边形内部的点数为a，边上的点数为b，那么满足：
S = a + b/2 - 1

凸包

给出一个二维平面内的点集，如果任意两个点的连线都在点集内，则这个点集是个凸集
对于给定的散点集X，包含X的所有凸集的交集S叫做X的凸包
点就是墙上的钉子，用一个橡皮筋套在外面，收缩后形成的凸多边形就是凸包

求点集的凸包

水平法：

凸包一般使用水平法求解
将凸包分为上凸壳和下凸壳两部分，分别求解
每一部分按照x的坐标排序，用单调栈维护，利用叉积的符号判断凹凸性

增量法：

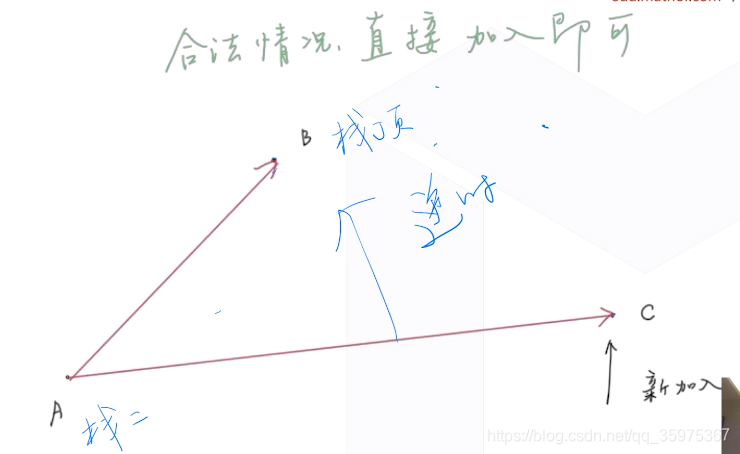
判断情况：
此时B合法

此时B不合法

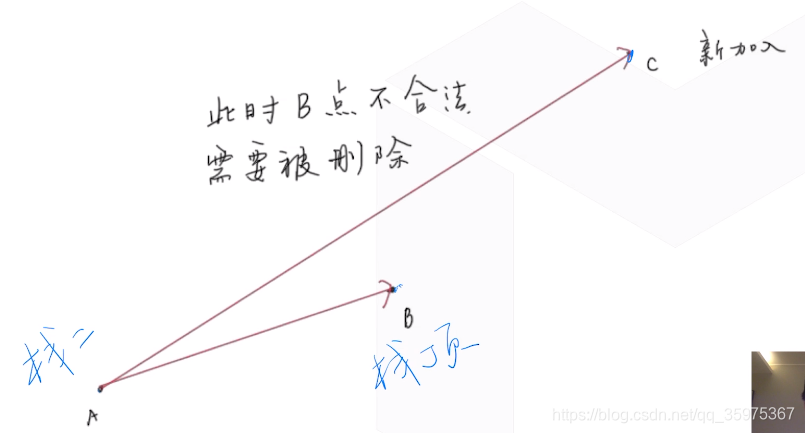
不合法的点一定是最后添加入S的，且是连续的

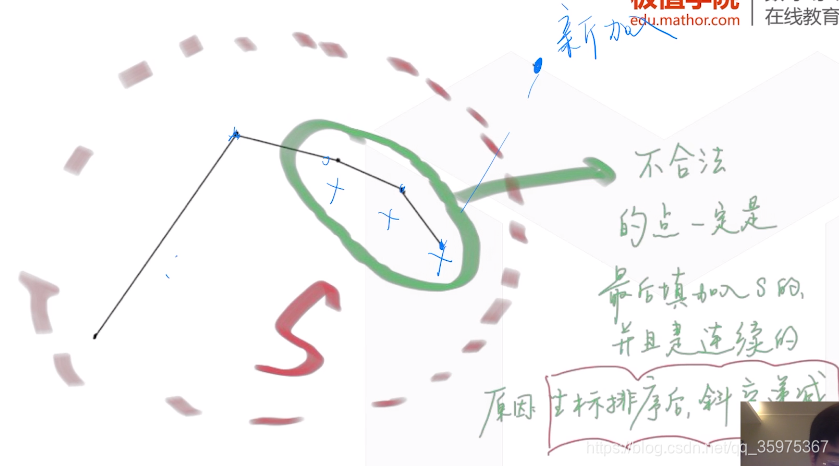
//判断上凸包
sort(poly.begin(),poly.end(),cmp);
int top=0,n=poly.size();
Stack[++top]=poly[0];
for(int i=1;i<n;i++)
{point C=poly[i];while(top>1){point B=Stack[top];point A=Stack[top-1];point AB=B-A;point AC=C-A;if((AB^AC)>eps)top--;else break;}Stack[++top]=C;
}

半平面

• 顾名思义，就是平面的一半。一条直线会把平面分成两部分，就 是两个半平面。对于半平面，我们可以用直线方程式如： ax+by+c > 0 表示，更常用的是用直线表示

半平面交

• 顾名思义，就是多个半平面求交集。其结果可能是一个凸多边形、 无穷平面、直线、线段、点等。 • 什么时候需要半平面交？
• 1. 二维线性规划 （高中数学）
• 2. 求多边形的核 • 多边形的核：如果多边形中存在一个区域使得在区域中可以看到 多边形中任意位置（反之亦然），则这个区域就是多边形的核

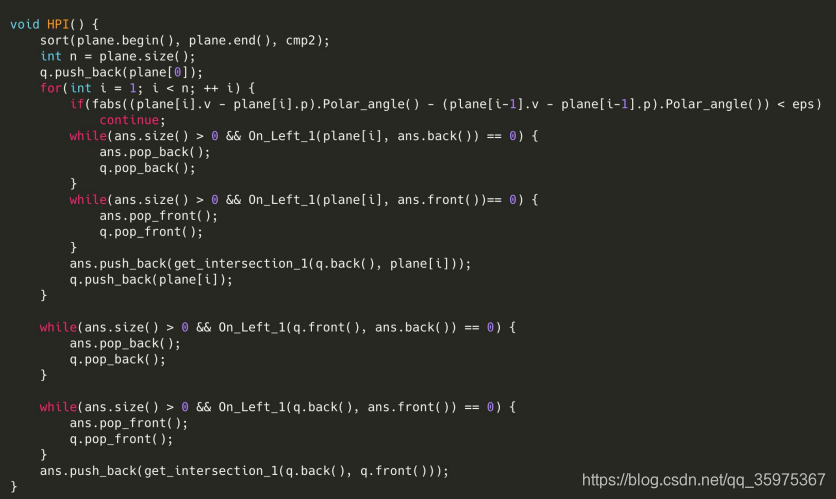
求半平面交

• 理论上有很多很多种求法，但是在实际应用中效率最高而且最好 写的是 S&I 增量法，也就是一个一个插入半平面并且更新答案。
• 核心思想：
• 1. 选取逆时针方向为正方向，把所有的直线变成向量。
• 2. 所有的向量按照极角排序，角度相同的保留左边的。
• 3. 按照顺序每次插入一个平面，删掉右面的部分，保留左边的部 分。
###具体方法：
1.选方向，排序（如上文）
• 2.用双端队列保存构成当前核的所有向量。
• 3.按照顺序遍历所有向量，每次加入判断影响
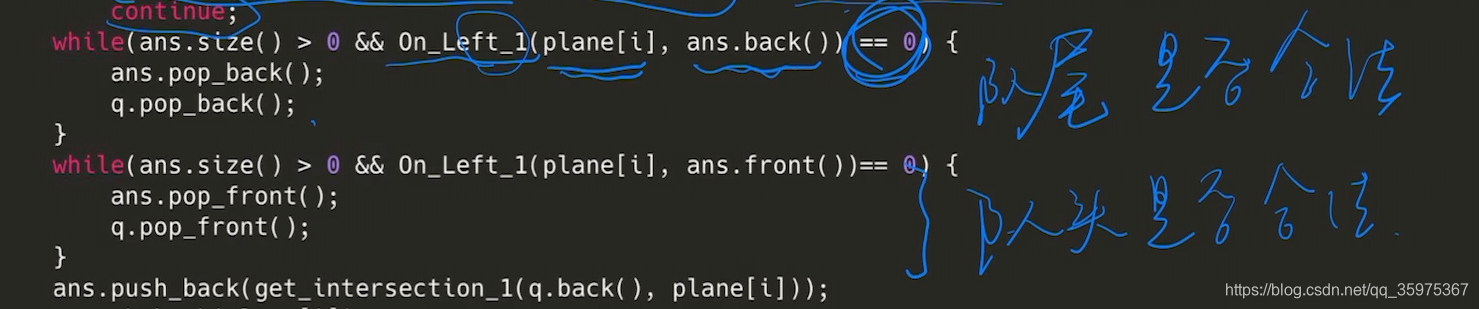
• 假设队列中最后两条直线的交点是左图所示。如果新加入了直线 后原来的交点在直线右侧，说明最后一条直线没有用，把它从队 列中删除。


看遍边6要不要保留，就看5和6的交点在直线的哪一侧

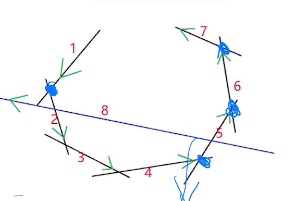
由p指向v的向量
ans存的交点
q存的边