NC 106056 poj1459 Power Network

题目大意：

总共有n个节点，其中有发电站np个、用户nc个和调度器n-np-nc个三种节点，每个发电站有一个最大发电量，每个用户有个最大接受电量，现在有m条有向边，边有一个最大的流量代表，最多可以流出这么多电，现在从发电站发电到用户，问最多可以发多少电
• N<=100

题解：

• 我们之前讲的网络流都是单源单汇问题，这题是多源多汇，关键在于把多源多汇问题转化为单源单汇，只要构造一个超级源点和一个超级汇点就ok了，把超级源点和各个源点之间加一条边，把各个汇点和超级汇点之间加一条边，这样就搞定了

NC213817 [网络流24题]最小路径覆盖问题

题目：

• 给定有向图G=(V,E)。设P 是G 的一个简单路（顶点不相交）的集合。如果V 中每个顶点恰好在P 的一条路上，则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始，长度也是任意的，特别地，可以为0。G 的最小路径覆盖是G 的所含路径条数最少的路径覆盖。
设计一个有效算法求一个有向无环图G 的最小路径覆盖。
• 1≤n≤150,1≤m≤6000

题解：

• 每个点用一次——
• 每个点拆成出点和入点，入点向出点连容量为1的边
• 原图中存在x到y的边的话，就从x的出点向y的入点连容量为1的边
• S向每个点的入点连容量为1的边，每个点的出点向T连容量为1的边

一张图中，路径数（点不重复）=点数-点之间匹配数（连边且不重复，也就是网络最大流）。
在网络流上体现为：最小路径覆盖=点的总数-网络最大流

例2：NC213818 [网络流24题]魔术球问题

题目：

• 假设有n根柱子，现要按下述规则在这n根柱子中依次放入编号为1，2，3，…的球。
（1）每次只能在某根柱子的最上面放球。
（2）在同一根柱子中，任何2个相邻球的编号之和为完全平方数。
试设计一个算法，计算出在n根柱子上最多能放多少个球。例如，在4 根柱子上最多可放11 个球。
编程任务：对于给定的n，计算在n根柱子上最多能放多少个球。
• 1≤n≤55

题解：

首先思想很重要，不是明显的图论，要往图论方向靠

建图方式：
S与左图所有数相连，右图所有数与T相连

对于一个进来的编号的球x，有两个选择：
第一个选择是放在某个和他能组成平方数的球（我们起名为y）的后面
第二个选择是自己单独出来成为开头
对于第一种选择，当然要y和x连一个边
对于第二种选择，S要和x连一个边
当然我们也要让x与T连一个边
但是一个点怎么能同时连多个，显然一个点是不够用的
我们将一个点给分开，分为x和x’
x与s相连，x’与t相连
为了满足第一种情况，对于满足条件的x和y两个点，连接y和x’
这样组成的图直接跑最大流算法即可
球和柱子同时加，跑出的最大流为省掉的柱子数，如果加入一个数当前最大流没有变化，说明柱子数+1，如果最大流+1，说明可以省下一个柱子、

方法2：

匈牙利算法也可以做
给定了柱子数n（最小路径覆盖数）以及放球条件（建边条件），求最多有多少个球（最多有多少个点可以满足这个最小路径覆盖数）。
枚举球的数量。
每来一个球（点）m，枚举1…m-1的每个点i，若i+m满足建边条件（和为完全平方数）则按以下方式建边——
套路拆点，每个点i拆成Xi、Yi，对于一组i、m，连Xi<->Y(m+5000)双向，跑匈牙利算出最大匹配。
根据二分图相关定理：最小路径覆盖数=点数-最大匹配数。
算出当前图的最小路径覆盖k，与给定柱子数比较。
k<n，继续加球。

k=n，可能还有更大的答案，继续加球。

k>n，m-1就是答案，停止加球。

输出路径，遍历1…m-1每个X部点，向其匹配点走，直到无路可走，沿路标记为已遍历。

已遍历过的X部点不再遍历。

NC 213820 [网络流24题]最长递增子序列问题

题目:

• 给定正整数序列x1 ,… , xn。 （1）计算其最长递增子序列的长度s。 （2）计算从给定的序列中最多可取出多少个长度为s的递增子序列。
（3）如果允许在取出的序列中多次使用x1和xn，则从给定序列中最多可取出多少个长度为s
的递增子序列。
• 编程任务：设计有效算法完成（1）（2）（3）提出的计算任务。
• 1≤n≤500

题解：

参考自众多大佬题解
第一问好说，经典dp问题，
F[i]，表示以第i位为开头的最长上升序列的长度
第二三问是网络流问题
因为题目要求是不下降序列，所以我们可以将不下降序列中的数字连边

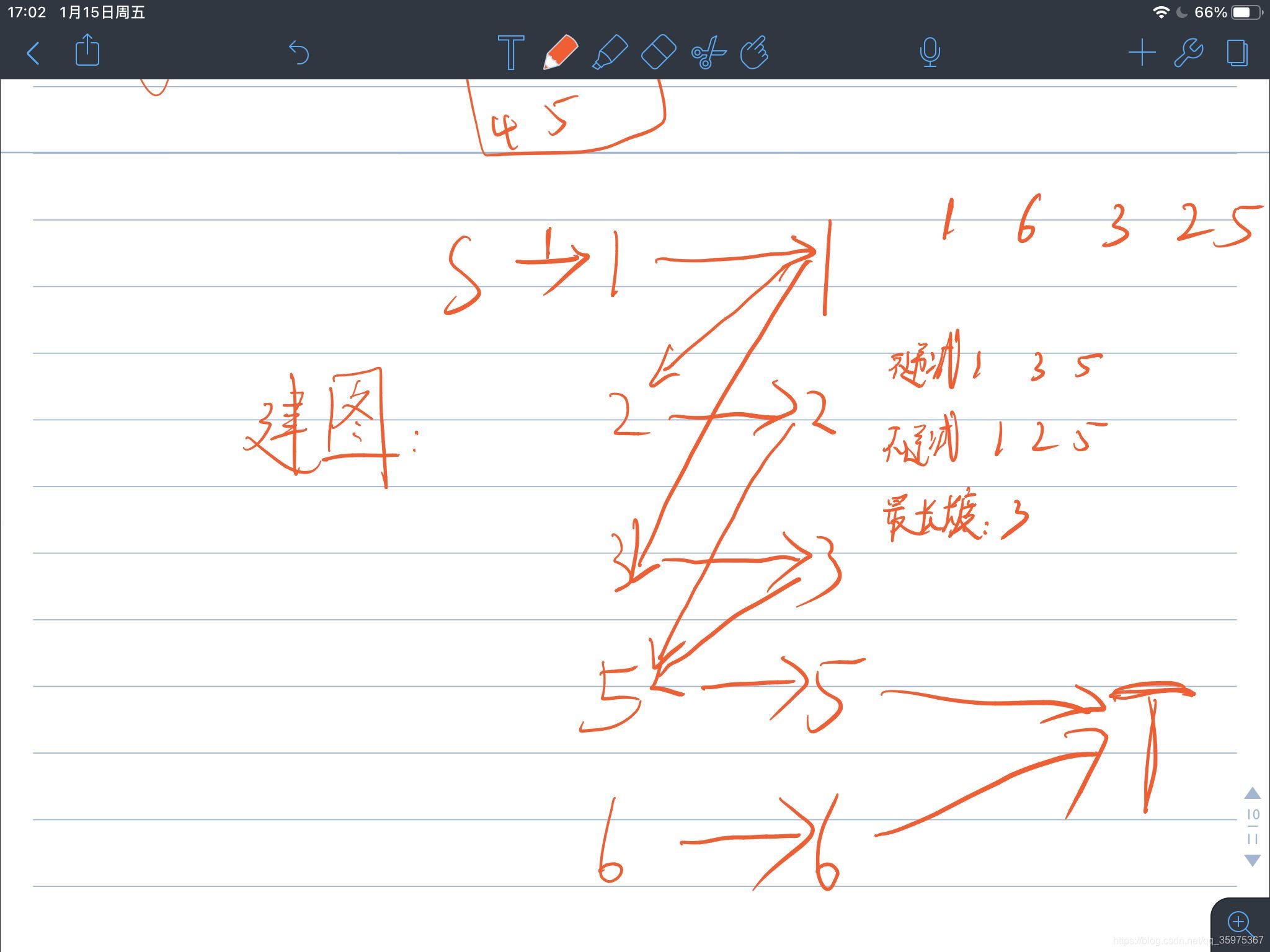
建图方式：

1. 我们先将每个数字x拆成两个x1，x2，两者连有一个容量为1的有向边，从x1到x2
2. 建立源点S和汇点T，如果序列第x位有F[x]=K,也就是第x位为最长序列的第一个数字，那么就建立S到x1连接一条容量为1的有向边
3. 如果F[i] = 1,从i2到T连接一个容量为1的有向边
4. 如果i<j且A[i] < A[j]且F[i]=F[j]+1，从<i.b>到<j.a>连接一条容量为1的有向边。也就是对于一个非递减序列<a,b>,我们连接a2到b1一条有向边，容量为1
   对于第二问，我们直接求网络最大流即可
   对于第三位，我们将边<1₁,1₂>,<n₁,n₂>,<S,1_`>,<n₂,T>
   四个边的容量改成无限大，再跑网络最大流即可
   对于一组数 1 6 3 2 5
   对其建边情况如下：
   

NC19939 [CQOI2015]网络吞吐量

题目：

• 路由是指通过计算机网络把信息从源地址传输到目的地址的活动，也是计算机网络设计中的重点和难点。网络中实现路由转发的硬件设备称为路由器。为了使数据包最快的到达目的地，路由器需要选择最优的路径转发数据包。例如在常用的路由算法OSPF(开放式最短路径优先)中，路由器会使用经典的Dijkstra算法计算最短路径，然后尽量沿最短路径转发数据包。
• 现在，若已知一个计算机网络中各路由器间的连接情况，以及各个路由器的最大吞吐量（即每秒能转发的数据包数量），假设所有数据包一定沿最短路径转发，试计算从路由器1到路由器n的网络的最大吞吐量。计算中忽略转发及传输的时间开销，不考虑链路的带宽限制，即认为数据包可以瞬间通过网络。路由器1到路由器n作为起点和终点，自身的吞吐量不用考虑，网络上也不存在将1和n直接相连的链路。
• n<=500，m<=100000

题解：

第一反应是最小费用最大流，但其实并不是
题目要求的是在最短路的基础上求最大吞吐量
若我们要走1到n的最短路，那我们只能走dis[v]=dis[u]+edge[u][v]的边
所以我们第一步就跑遍最短路，保留最短路中的边，此时边权我们就可以忽略掉了，因为之后再也用不上
题目中吞吐量的限制与平常不一样，这里不是对边而是对点，对点的话没办法直接算，我们可以将点一分为二，将n个点拆成n*2个点，然后第i个点向第i+n个点建立一个容量为A[i]的边
然后对于最短路中的边e[u][v]，我们从第u+n个点向第v个点建一条容量为inf的边
从源点s向点1建一条容量为inf的边
从点2n向汇点t建立一条容量为inf的边
然后跑最大流即可
本题的特殊之处就在于先用最短路处理一下，剩下的步骤都是最大流常规操作了、

代码：