引言
通常,服务所公开的资源和 API 必须仅限受信任的特定用户和客户端访问。那进行 API 级别信任决策的第一步就是身份认证——确定用户身份是否可靠。
在微服务场景中,身份认证通常统一处理。一般有两种实现形式:
基于API 网关中心化认证:要求客户端必须都通过网关访问微服务。(这就要求提供一种安全机制来认证请求是来自于网关。)
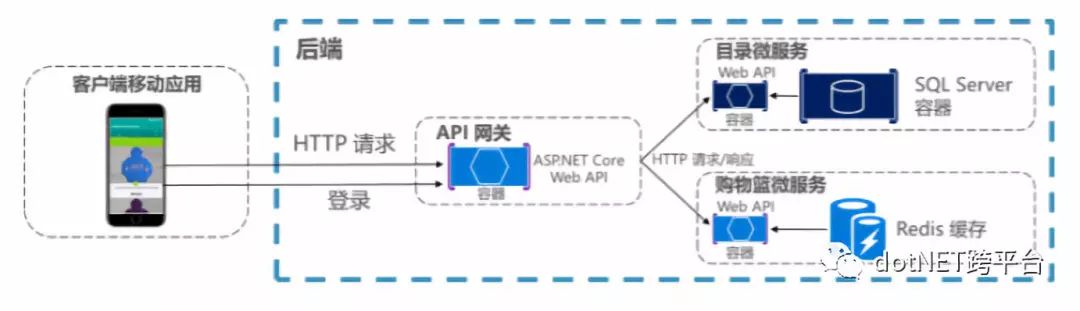
基于安全令牌服务(STS)认证:所有的客户端先从STS获取令牌,然后请求时携带令牌完成认证。
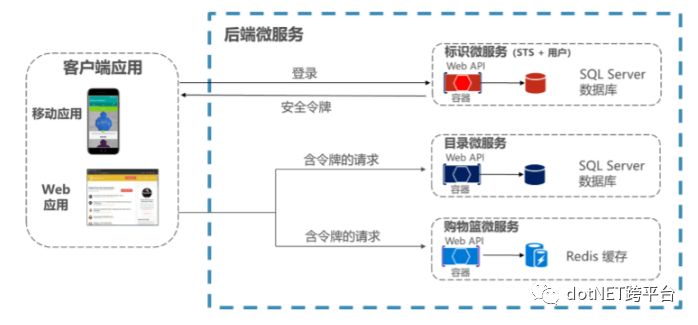
Identity Service就是使用第二种身份认证方式。
服务简介
Identity microservice 主要用于统一的身份认证和授权,为其他服务提供支撑。
提到认证,大家最熟悉不过的当属Cookie认证了,它也是目前使用最多的认证方式。但Cookie认证也有其局限性:不支持跨域、移动端不友好等。而从当前的架构来看,需要支持移动端、Web端、微服务间的交叉认证授权,所以传统的基于Cookie的本地认证方案就行不通了。我们就需要使用远程认证的方式来提供统一的认证授权机制。
而远程认证方式当属:OAuth2.0和OpenID Connect了。借助OAuth2.0和OpenID Connect即可实现类似下图的认证体系:
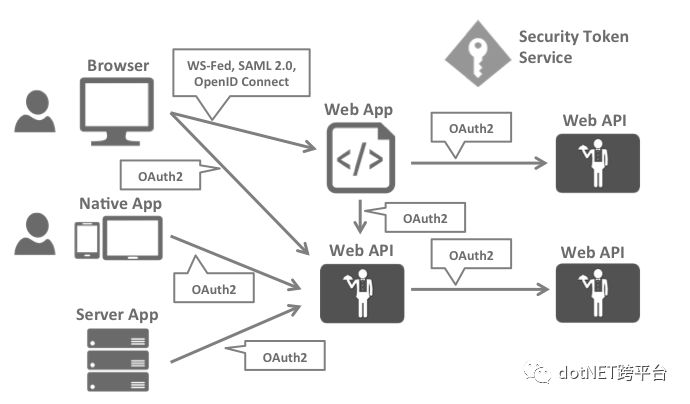
而如何实现呢,借助:
ASP.NET Core Identity
IdentityServer4
基于Cookie的认证和基于Token的认证的差别如下所示:
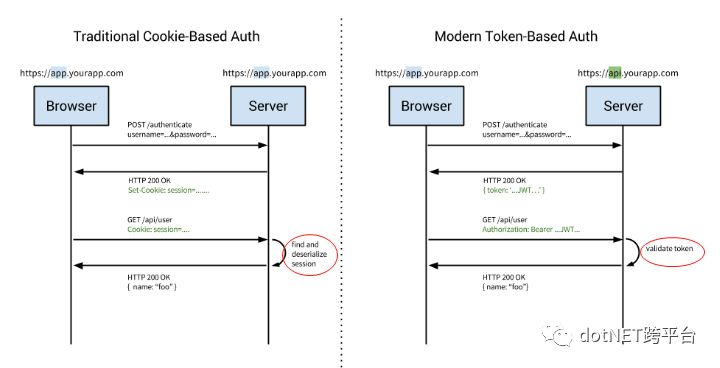
架构模式
从目录结构可以看出它是一套MVC单层架构的网站。我们可以单独进行运行和调试,也可以把它放进自己的项目中。
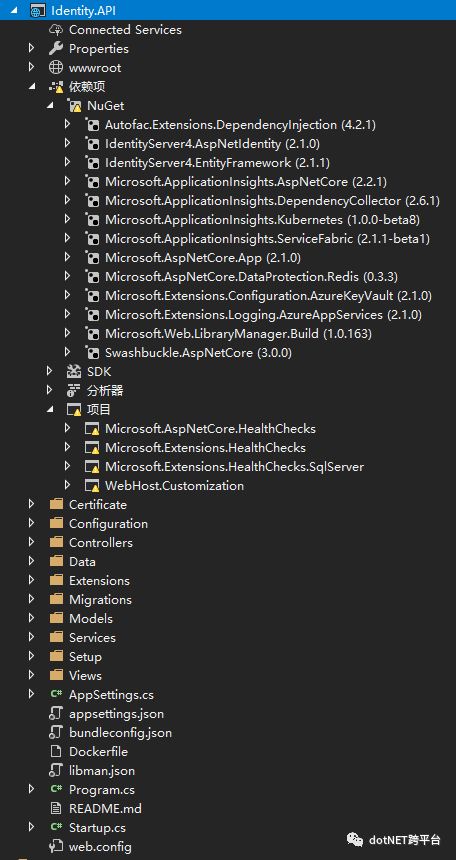
主要依赖:
1、HealthCheck 健康检查
2、WebHost
3、Entity Framework
4、Autofac
5、IdentityServer4
6、其中IdentityServer4.AspNetIdentity又用到了ASP.NET Core Identity
启动流程
Program.cs
Main函数:


BuildWebHost函数:

其中有一个UseHealthChecks,这是一个对项目健康的检查。
健康检查,其实这个名称已经很明确了,它是检查你的应用程序是否健康运行的一种方式。随着当前各类项目越来越多的应用程序正在转向微
服务式架构,健康检查就变得尤为关键。虽然微服务体系结构具有许多好处,但其中一个缺点就是为了确保所有这些服务都正常运行的操作开销
更高。你不在是监视一个庞大的整体项目的健康状况,而是需要监控许多不同服务的状态,甚至这些服务通常只负责一件事情。健康检查(Heatlh
Checks)通常与一些服务发现工具结合使用,如Consul ,来监控您的微服务器,来观测您的服务是否健康运行。
健康检查有很多种不同的方法,但最常见的方法是将HTTP端点暴露给专门用于健康检查的应用程序。一般来说,如果一切情况都很好,你的服
务将返回200的状态码,然而任何非200的代码则意味着出现问题。例如,如果发生错误,你可能会返回500以及一些出错的JSON信息。


ASP.NET Core Identity && IdentityServer4简介
ASP.NET Core Identity用于构建ASP.NET Core Web应用程序的成员资格系统,包括成员资格,登录和用户数据(包括登录信息、角色和声明)。
ASP.NET Core Identity封装了User、Role、Claim等身份信息,便于我们快速完成登录功能的实现,并且支持第三方登录(Google、Facebook、QQ、Weixin等,支持开箱即用[第三方身份提供商列表]),以及双重验证,同时内置支持Bearer 认证(令牌认证)。
虽然ASP.NET Core Identity已经完成了绝大多数的功能,且支持第三方登录(第三方为其用户颁发令牌),但若要为本地用户颁发令牌,则需要自己实现令牌的颁发和验证逻辑。换句话说,我们需要自行实现OpenId Connect协议。
OpenID Connect 1.0 是基于OAuth 2.0协议之上的简单身份层,它允许客户端根据授权服务器的认证结果最终确认终端用户的身份,以及获取基本的用户信息。
而IdentityServer4就是为ASP.NET Core量身定制的实现了OpenId Connect和OAuth2.0协议的认证授权中间件。IdentityServer4在ASP.NET Core Identity的基础上,提供令牌的颁发验证等。
相关知识:
OAuth 2.0 简介
OpenID Connect 简介
Identity Server 4
认证流程
在ASP.NET Core中使用的是基于申明(Claim)的认证,而什么是申明(Cliam)呢?
Claim 是关于一个人或组织的某个主题的陈述,比如:一个人的名称,角色,个人喜好,种族,特权,社团,能力等等。它本质上就是一个键值对,是一种非常通用的保存用户信息的方式,可以很容易的将认证和授权分离开来,前者用来表示用户是/不是什么,后者用来表示用户能/不能做什么。在认证阶段我们通过用户信息获取到用户的Claims,而授权便是对这些的Claims的验证,如:是否拥有Admin的角色,姓名是否叫XXX等等。
认证主要与以下几个核心对象打交道:
Claim(身份信息)
ClaimsIdentity(身份证)
ClaimsPrincipal (身份证持有者)
AuthorizationToken (授权令牌)
IAuthenticationScheme(认证方案)
IAuthenticationHandler(与认证方案对应的认证处理器)
IAuthenticationService (向外提供统一的认证服务接口)
那其认证流程是怎样的呢?
1、用户打开登录界面,输入用户名密码先行登录,服务端先行校验用户名密码是否有效,有效则返回用户实例(User)。
2、这时进入认证准备阶段,根据用户实例携带的身份信息(Claim),创建身份证(ClaimsIdentity),然后将身份证交给身份证持有者(ClaimsPrincipal)持有。
3、接下来进入真正的认证阶段,根据配置的认证方案(IAuthenticationScheme),使用相对应的认证处理器(IAuthenticationHandler)进行认证 。认证成功后发放授权令牌(AuthorizationToken)。该授权令牌包含后续授权阶段需要的全部信息。
授权流程
授权就是对于用户身份信息(Claims)的验证,,授权又分以下几种种:
基于Role的授权
基于Scheme的授权
基于Policy的授权
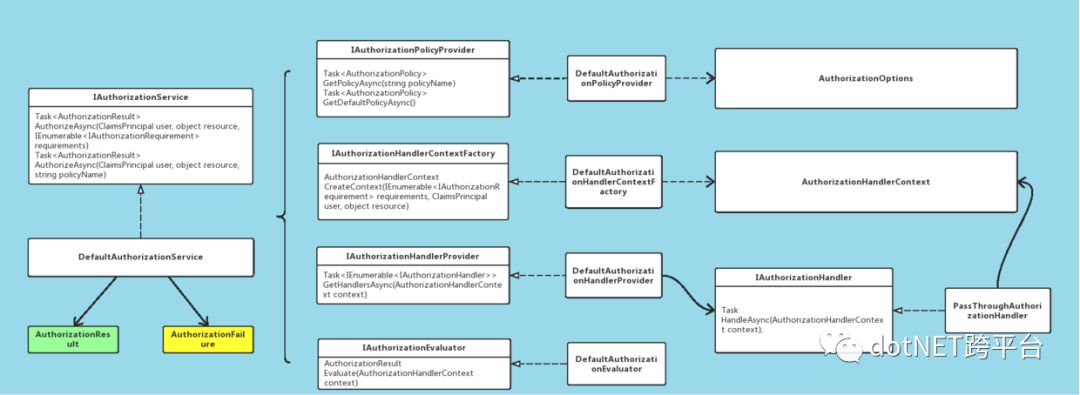
授权主要与以下几个核心对象打交道:
IAuthorizationRequirement(授权条件)
IAuthorizationService(授权服务)
AuthorizationPolicy(授权策略)
IAuthorizationHandler (授权处理器)
AuthorizationResult(授权结果)
那授权流程是怎样的呢?
当收到授权请求后,由授权服务(IAuthorizationService)根据资源上指定的授权策略(AuthorizationPolicy)中包含的授权条件(IAuthorizationRequirement),找到相对应的授权处理器(IAuthorizationHandler )来判断授权令牌中包含的身份信息是否满足授权条件,并返回授权结果。
中间件集成
回过头来我们再来刷一遍startup代码中是怎么集成进Identity service的。
1. 首先是映射自定义扩展的User和Role
// 映射自定义的User,Roleservices.AddIdentity<ApplicationUser, IdentityRole>().AddEntityFrameworkStores<ApplicationDbContext>()//配置使用EF持久化存储.AddDefaultTokenProviders();//配置默认的TokenProvider用于变更密码和修改email时生成Token
2. 配置IdentityServer服务

使用AddConfigurationStore和AddOperationalStore扩展方法就是用来来指定配置数据和操作数据基于EF进行持久化。
3. 添加IdentityServer中间件
app.UseIdentityServer(); 4. 预置种子数据
需要预置Client和Resource写在Config.cs文件中,他们又是中main函数中被MigrateDbContext使用的。
GetClients

IdentityResources
身份资源是用户ID、姓名或电子邮件地址等数据
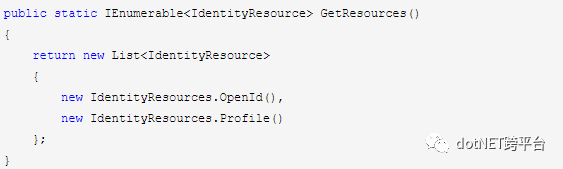
ApiResources

5. 迁移数据库上下文
IdentityServer为配置数据和操作数据分别定义了DBContext用于持久化,配置数据对应ConfigurationDbContext,操作数据对应PersistedGrantDbContext。详细看main函数。
这篇文章使用了园子里『___知多少』文章对不少内容,表示感谢,原文链接eShopOnContainers 知多少[3]:Identity microservice。
相关文章:
eShopOnContainers 看微服务 ①:总体概览
eShopOnContainers 看微服务 ②:配置 启动
eShopOnContainers 知多少[1]:总体概览
eShopOnContainers 知多少[2]:Run起来
eShopOnContainers 知多少[3]:Identity Microservice
eShopOnContainers 知多少[4]:Catalog microservice
Catalog Service - 解析微软微服务架构eShopOnContainers(三)
eShopOnContainers 知多少[5]:EventBus With RabbitMQ
EventBus In eShop -- 解析微软微服务架构eShopOnContainers(四)
eShopOnContainers 是一个基于微服务的.NET Core示例框架
原文地址:https://www.cnblogs.com/tianyamoon/p/10081277.html
.NET社区新闻,深度好文,欢迎访问公众号文章汇总 http://www.csharpkit.com

![P2168 [NOI2015] 荷马史诗(哈夫曼编码树)](http://pic.xiahunao.cn/P2168 [NOI2015] 荷马史诗(哈夫曼编码树))



虚树(初步了解))
![P2048 [NOI2010] 超级钢琴(RMQ 贪心)](http://pic.xiahunao.cn/P2048 [NOI2010] 超级钢琴(RMQ 贪心))

![[SDOI2011]消耗战](http://pic.xiahunao.cn/[SDOI2011]消耗战)

![P4716-[模板]最小树形图](http://pic.xiahunao.cn/P4716-[模板]最小树形图)
![P1081 [NOIP2012 提高组] 开车旅行(倍增)(动态规划)](http://pic.xiahunao.cn/P1081 [NOIP2012 提高组] 开车旅行(倍增)(动态规划))



![P3426-[POI2005]SZA-Template【KMP】](http://pic.xiahunao.cn/P3426-[POI2005]SZA-Template【KMP】)

(费马小定理)(线性求逆元))
)
![P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包](http://pic.xiahunao.cn/P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包)
(ybtoj))