ServiceMesh(服务网格) 概念在社区里头非常火，有人提出 2018 年是 ServiceMesh 年，还有人提出 ServiceMesh 是下一代的微服务架构基础。

那么到底什么是 ServiceMesh？它的诞生是为了解决什么问题？企业是否适合引入 ServiceMesh？

 

微服务架构的核心技术问题

 

在业务规模化和研发效能提升等因素的驱动下，从单块应用向微服务架构的转型 (如下图所示)，已经成为很多企业 (尤其是互联网企业) 数字化转型的趋势。

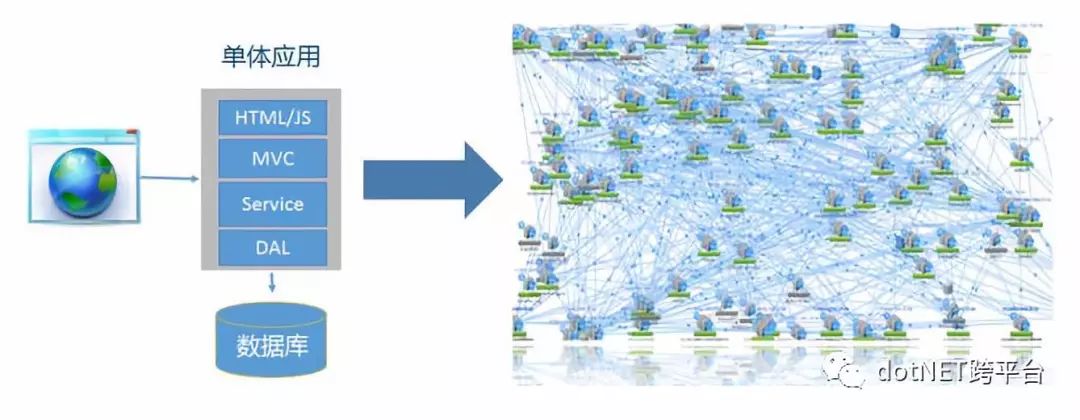
在微服务模式下，企业内部服务少则几个到几十个，多则上百个，每个服务一般都以集群方式部署，这时自然产生两个问题 (如下图所示)：

 

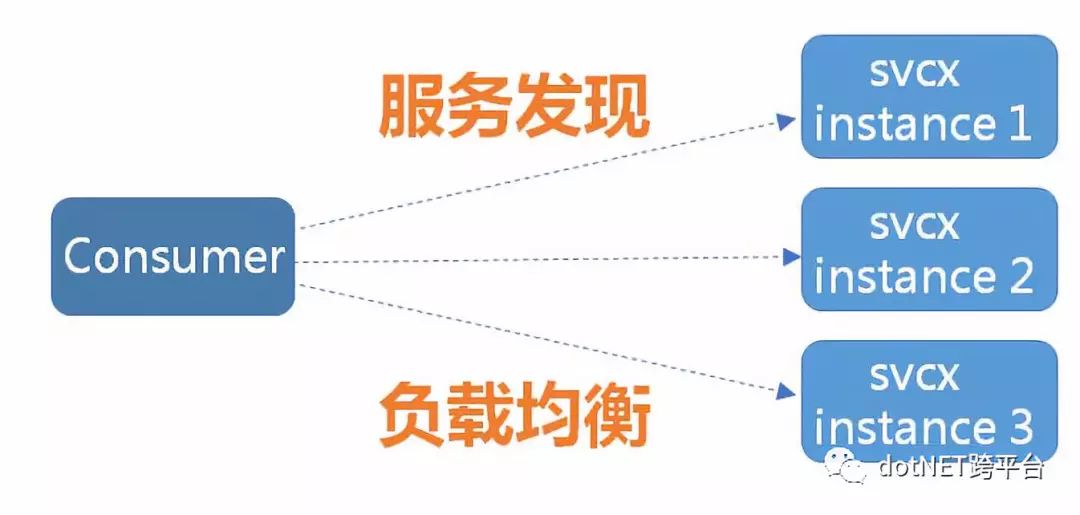
一、服务发现： 服务的消费方 (Consumer) 如何发现服务的提供方 (Provider)？

二、负载均衡： 服务的消费方如何以某种负载均衡策略访问集群中的服务提供方实例？

作为架构师，如果你理解了这两个问题，也就理解了微服务架构在技术上最核心问题。

 

三种服务发现模式

 

服务发现和负载均衡并不是新问题，业界其实已经探索和总结出一些常用的模式，这些模式的核心其实是代理 (Proxy，如下图所以)，以及代理在架构中所处的位置。

 

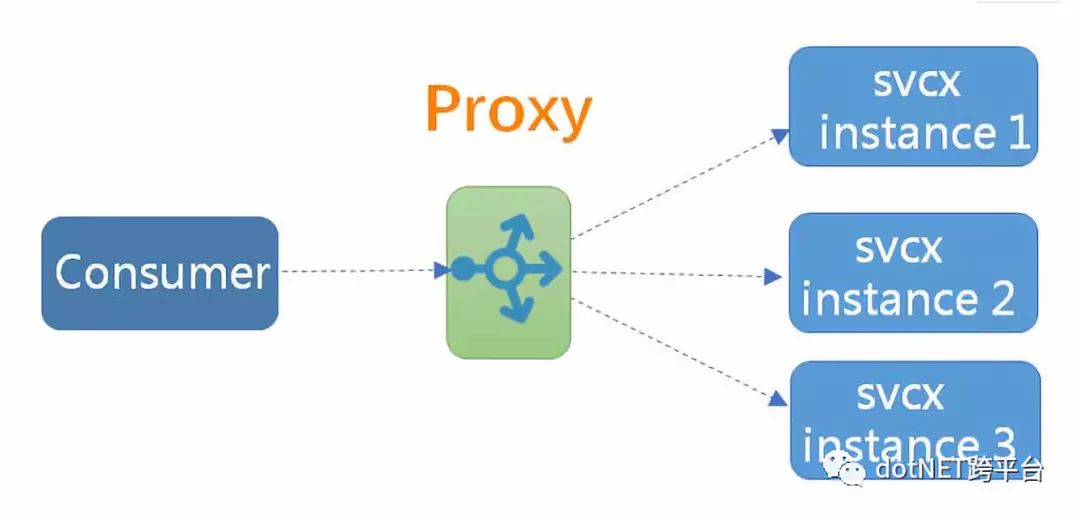
在服务消费方和服务提供方之间增加一层代理，由代理负责服务发现和负载均衡功能，消费方通过代理间接访问目标服务。根据代理在架构上所处的位置不同，当前业界主要有三种不同的服务发现模式：

模式一：传统集中式代理

 

 

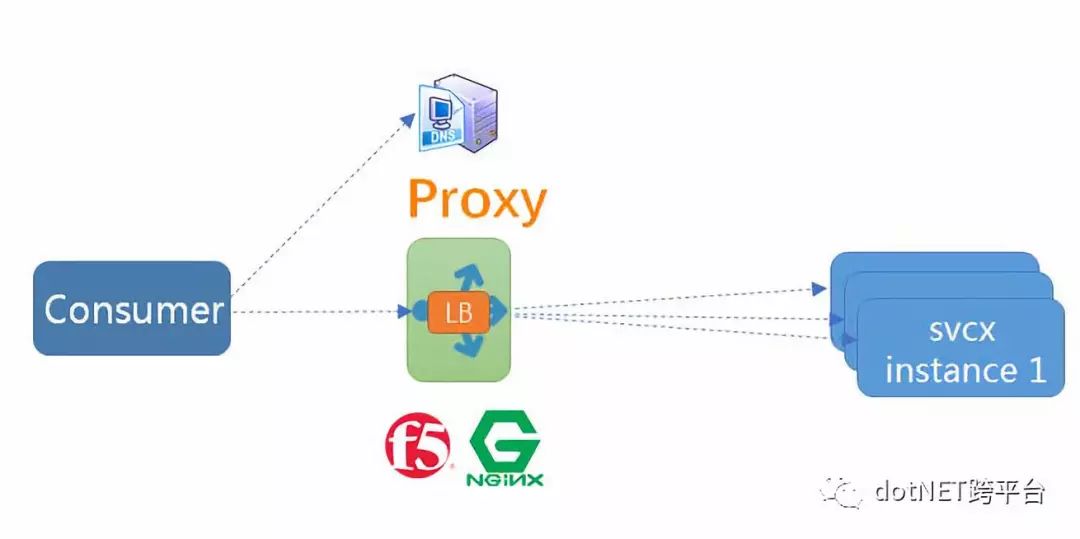
这是最简单和传统做法，在服务消费者和生产者之间，代理作为独立一层集中部署，由独立团队 (一般是运维或框架) 负责治理和运维。常用的集中式代理有硬件负载均衡器 (如 F5)，或者软件负载均衡器 (如 Nginx)，F5(4 层负载)+Nginx(7 层负载) 这种软硬结合两层代理也是业内常见做法，兼顾配置的灵活性 (Nginx 比 F5 易于配置)。

这种方式通常在 DNS 域名服务器的配合下实现服务发现，服务注册 (建立服务域名和 IP 地址之间的映射关系) 一般由运维人员在代理上手工配置，服务消费方仅依赖服务域名，这个域名指向代理，由代理解析目标地址并做负载均衡和调用。

国外知名电商网站 eBay，虽然体量巨大，但其内部的服务发现机制仍然是基于这种传统的集中代理模式，国内公司如携程，也是采用这种模式。

模式二：客户端嵌入式代理

 

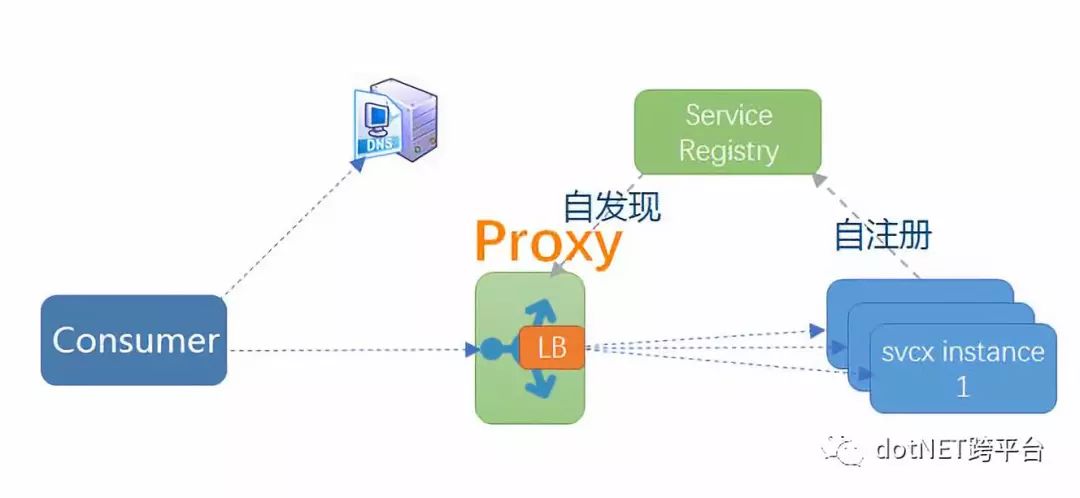
这是很多互联网公司比较流行的一种做法，代理 (包括服务发现和负载均衡逻辑) 以客户库的形式嵌入在应用程序中。这种模式一般需要独立的服务注册中心组件配合，服务启动时自动注册到注册中心并定期报心跳，客户端代理则发现服务并做负载均衡。

Netflix 开源的 Eureka(注册中心)[附录 1] 和 Ribbon(客户端代理)[附录 2] 是这种模式的典型案例，国内阿里开源的 Dubbo 也是采用这种模式。

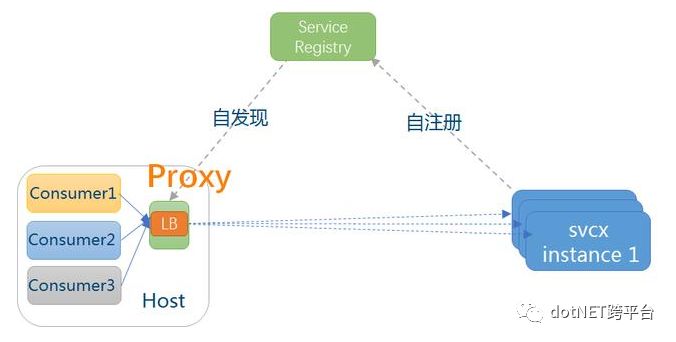
模式三：主机独立进程代理

这种做法是上面两种模式的一个折中，代理既不是独立集中部署，也不嵌入在客户应用程序中，而是作为独立进程部署在每一个主机上，一个主机上的多个消费者应用可以共用这个代理，实现服务发现和负载均衡，如下图所示。这个模式一般也需要独立的服务注册中心组件配合，作用同模式二。

阿里、微博、摩拜、唯品会等公司都在积极探索Service Mesh的架构模式，只是在实践中一般具备一定开发能力的公司都会选择基于Istio进行二次开发，如目前阿里开源的SOFAMesh/SOFAMosn两个项目。

 

 Service Mesh（服务网格）

 

 Service Mesh又称为服务网格，本质上就是我们前面介绍过的模式三。之所为称之为服务网格是因为按照模式三的结构，每个主机上同时运行了业务逻辑代码和代理，此时这个代理被形象地称之为SideCar（业务代码进程相当于主驾驶，共享一个代理相当于边车），服务之间通过SideCar发现和调用目标服务，从而形成服务之间的一种网络状依赖关系，然后通过独立部署的一种称之为控制平面（ControlPlane）的独立组件来集中配置这种依赖调用关系以及进行路由流量调拨等操作，如果此时我们把主机和业务逻辑从视觉图上剥离，就会出现一种网络状的架构，服务网格由此得名。

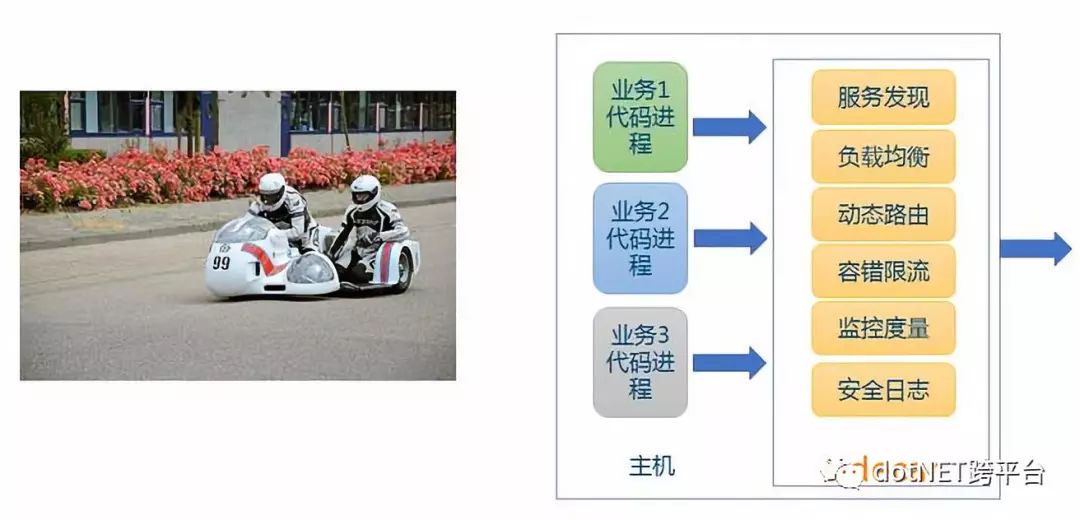
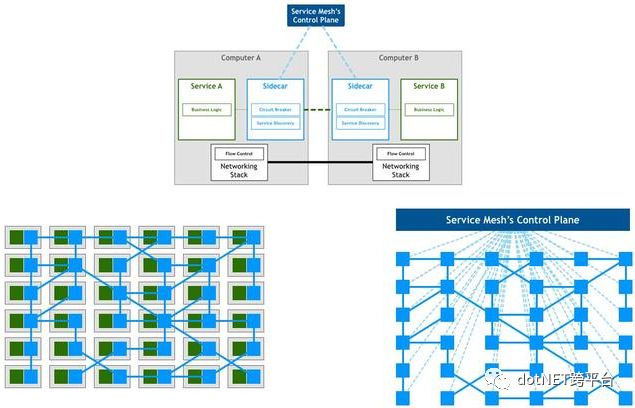
在新一代的Service Mesh架构中服务消费方和提供方的主机（或容器）两边都会部署代理SideCar，此时SideCar与服务所在的主机又称之为数据平面（DataPlane），与我们前面说到的用于依赖关系配置和流量调拨操作的控制平面相对应。

 

Istio

 

通过上述的内容，我们从概念上应该是大概理解了什么是Service Mesh。而具体要落地Service Mesh只有概念是远远不够的，相反，如果没有一种可落地执行的开源框架，这个概念也不会这么快被大家所接受。

 Istio就是目前受Google/IBM 等大厂支持和推进的一个 ServiceMesh开源框架组合。它解决了开发人员和运维人员在整体应用程序向分布式微服务体系结构过渡时所面临的挑战。我们知道无论是基于SpringCloud的微服务架构体系还是目前我们说到的Service Mesh，随着微服务规模的增长会带来很多的复杂性，如服务发现、负载均衡、故障恢复、监控,甚至A/B测试、访问控制等。而要对涉及这些问题的微服务架构体系进行管理，如果没有成熟的组件的话，就会需要耗费很多的精力去开发一些运维工具，而这个成本是非常高的。

 

而Istio则提供了一个完整的解决方案来满足微服务应用程序的各种需求。下图是Istio官网（https://istio.io）所展示的关于Istio的一张架构图：

 

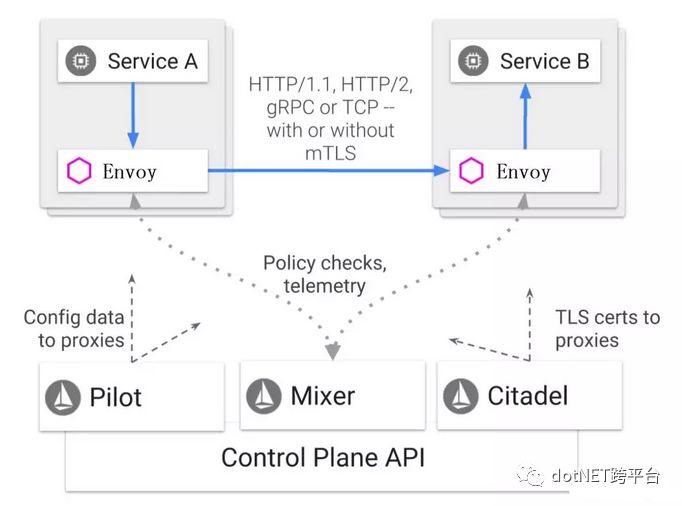
在这张架构图中Istio服务网格在逻辑上还是分为数据平面和控制平面。数据平面中的SideCar代理是由一款叫做Envoy的组件来承担的，它是一款用C++开发的高性能代理，用于协调服务网格中所有服务的入站和出站流量。

 

Envoy提供了很多内在的特性如：

• 动态服务发现

• 负载均衡

• TLS终止

• HTTP/2和gRPC代理

• 熔断器

• 健康检查

• 基于百分比的流量分割

• 故障注入

• 丰富的指标

 

从上面的特性上看实际上Envoy已经提供了很完备的SideCar的功能，只是由于其采用的是C++开发的，目前在国内的落地实践中会有不同的取舍和选择，如蚂蚁金服内部在实践的过程中就没有使用Istio默认集成的Envoy，而是用 Golang 开发了新的 Sidecar，已经开源的SOFAMosn，来替代 Envoy。

 

在Istio控制平面中的各个组件的作用如下：

• Mixer：负责收集代理上采集的度量数据，进行集中监控；

• Pilot：主要为SideCar提供服务发现、智能路由（如A/B测试）、弹性（超时、重试、断路器）的流量管理功能；

• Citadel：负责安全控制数据的管理和下发；

 

以上就是关于Istio及其组件的一些介绍，具体如何使用Istio进行服务开发及安装操作，大家可以看看Istio的官网，另外需要强调的是kubernetes是目前 Isito 主力支持的容器云环境。

 

Service Mesh的优势

 

事实上Service Mesh这种架构模式并不新鲜，很早就有公司进行过尝试，之所以最近又火起来的原因，主要还是因为模式一、模式二的确有一些固有的缺陷，模式一相对比较重，有单点问题和性能问题。

 

而模式二则有客户端复杂，支持多语言困难，路由、熔断、限流等服务操作无法集中治理的问题。而Service Mesh则正好弥补了二者的不足，它是纯分布式的，没有单点的问题，性能也比较优秀并且与开发语言无关，还可以集中进行治理。

 

此外，随着微服务化、多语言和容器化的发展趋势，很多公司也迫切需要一种轻量级的服务发现机制，加上一些大厂如Google/IBM的助推（如kubernetes与Docker的容器之争），正好Service Mesh迎合了这种趋势，所以才有今天火热的局面。

原文地址：https://www.cnblogs.com/tianyamoon/p/10106587.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com