正文

上一章我们讲了pod的hostip模式，但在生产环境中，我们都是通过service来访问k8s集群的，service有两种模式来暴漏端口，今天我们来分享一下

1.clusterIP模式

我们在创建service的时候，默认创建的时clusterIP模式，clusterIP模式的特点是只能在node节点上访问，创建方法如下：

1.1首先创建Deployment

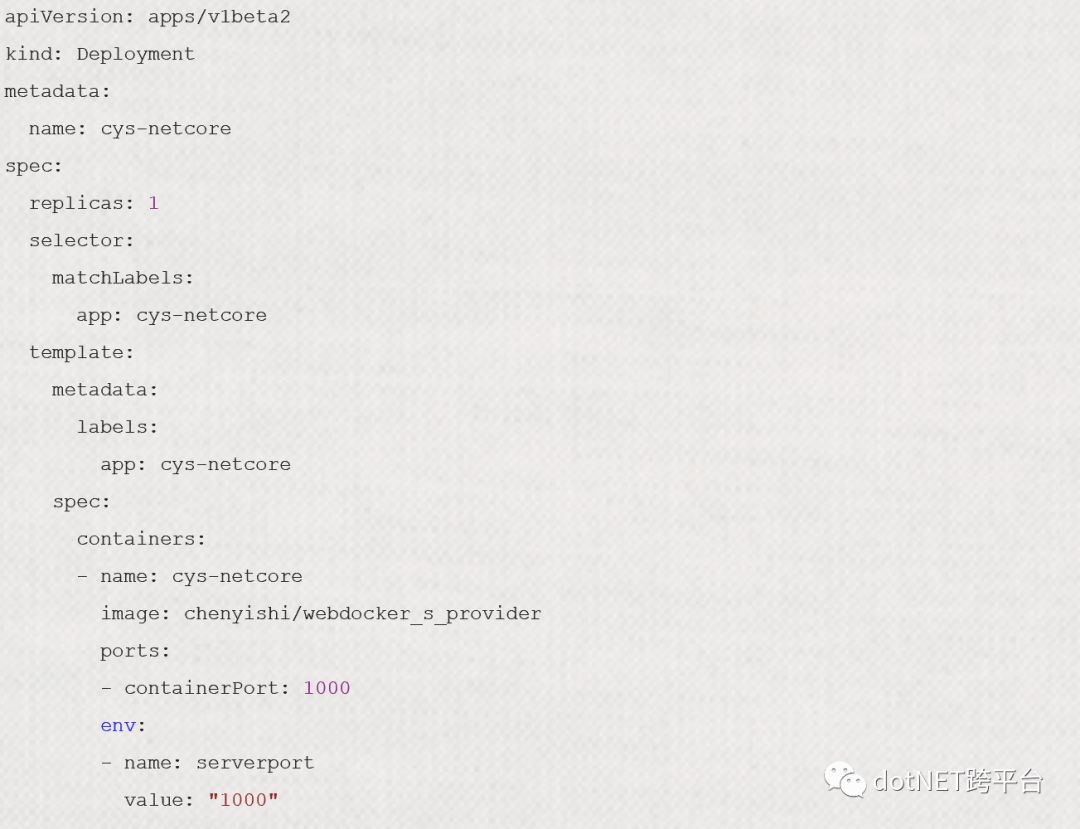
1.2创建service，并指定clusterip（不指定也可以，会自动随机分配）

注意：clusterIP设置须按照集群搭建时指定的范围设置，我们查看一下我们制定的范围

可以看到范围是10.10.10.1~10.10.10.255，编写yaml文件如下

可查看信息，如下

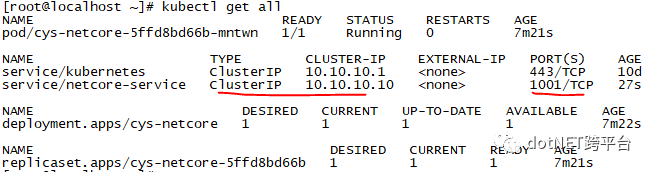
1.3验证地址

我们可以去node节点验证一下

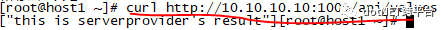
至此clusterip介绍完毕

回到顶部

2.NodePort模式

我们可以看到clusterIP模式只能在node节点访问，这无法满足我们的生产环境，因此我们在生产环境中都是采用NodePort模式，映射到宿主机的port，我们的Deployment的yaml文件还是采用上面的，需要改一下service的yaml文件

2.1创建service

查看信息

2.2验证

访问地址http://192.168.8.202:31111/api/values

 

成功访问！！！

相关文章：

• .net core 上 K8S(三)Yaml文件运行.netcore程序

• .net core i上 K8S(四).netcore程序的pod管理，重启策略与健康检查

• Docker最全教程——从理论到实战（一）

• Docker最全教程——从理论到实战（二）

• Docker最全教程——从理论到实战（四）

• Docker最全教程——从理论到实战（五）
  

• Docker最全教程——从理论到实战（六）
  

• Docker最全教程——从理论到实战（七）
  

原文地址：https://www.cnblogs.com/chenyishi/p/10121980.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com