来源： Using multiple instances of strongly-typed settings with named options in .NET Core 2.x
作者： Andrew Lock
译者： Lamond Lu

.NET Core从1.0版本开始，就已经开始使用Options模式绑定强类型配置对象。从那时起到现在，这个特性已经获得了更多的功能。例如在.NET Core 1.1中引入的IOptionsSnapshot类。使用这个类的好处是，当你的配置文件（例如: appsetting.json)发生变化时，它可以帮助我们自动刷新我们的强类型配置对象。

本篇博客中，我们将讨论在依赖注入容器中注册强类型配置的多个实例的几种方式。我将特别说明如何使用Named Options方式来完成注入。

使用强类型配置

Options模式将POCO对象和IConfiguration对象绑定，从而实现强类型配置。因为这一过程我已经在之前一篇博文中介绍过，所以这里我就简述一下。

我们可以将强类型配置对象和配置绑定起来，并注入到你的服务中。

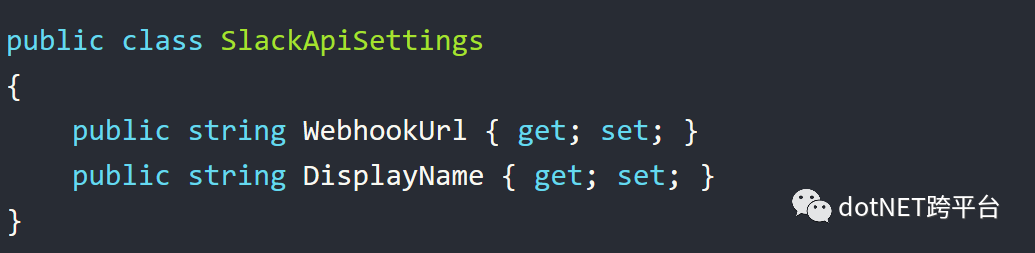
你可以在Startup类的ConfigureServices中使用Configure将强类型配置对象和配置中的一个节点绑定起来。

以上代码中，Configure方法将你的配置和SlackApiSettings对象绑定了起来。除了以上方式，Configure方法还提供了一个参数为Action的重载，所以你来可以使用如下的方式绑定配置。

你可以通过在服务中注入IOptions对象来访问配置好的SlackApiSettings对象。

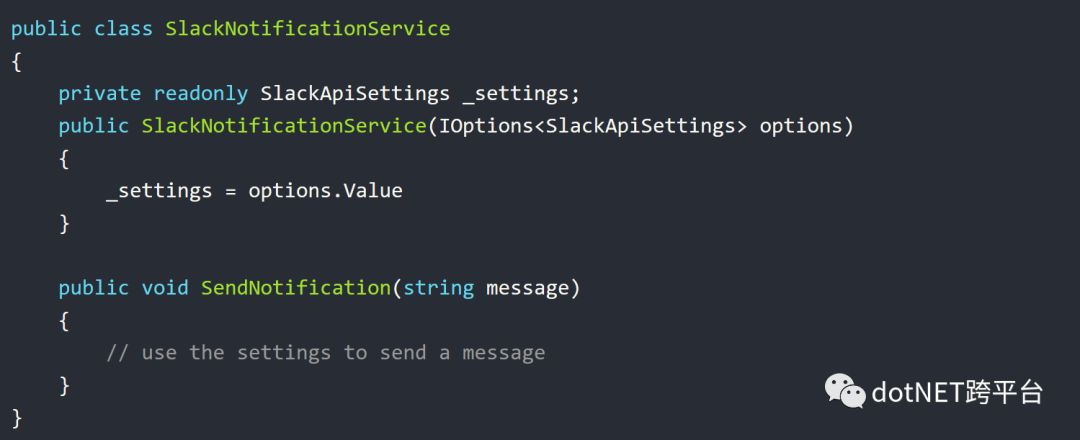
你可以使用IOptions.Value属性，获取到配置好的强类型对象。

除了以上方式，你还可以注入一个IOptionsSnapshot接口对象。

使用IOptionsSnapshot处理配置变化

到目前为止，我所展示的例子都是最典型的用法。但是当我们使用IOption来读取强类型配置时，这意味着你的配置在程序生命周期中是不变的。即配置对象只会计算和绑定一次。假如你在程序运行过程中，更改了appSettings.json文件，程序读取配置时，依然会得到程序启动时的配置对象，而非你修改过之后的配置对象。

对我个人而言，对于大部分场景，使用IOption已经能够解决所有问题。但是如果程序确实需要支持重新加载配置，我们还可以使用ASP.NET Core中的IOptionsSnapshot。IOptionsSnapshot和IOptions使用方法一样，因此你无需在应用程序中执行任何额外的操作。你只需要使用IOptionsSnapshot.Value属性读取配置对象即可。

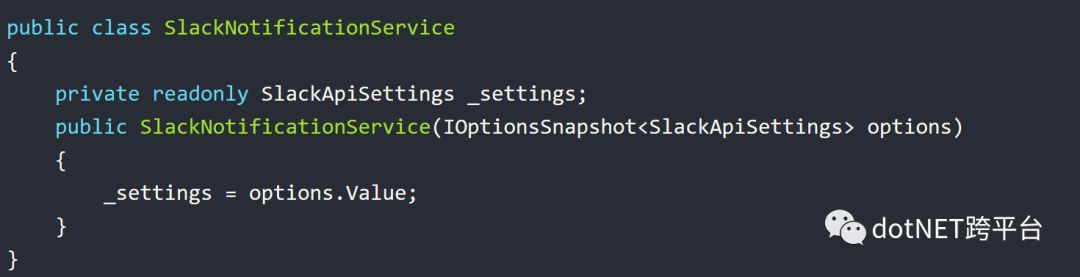
使用以上方式，如果你在程序启动后，修改了appSettings.json文件，IOptionsSnapshot会在下一次请求时，更新配置值，你就能获取到新的配置值了。这里需要注意的是配置值的生命周期是Scoped, 即在一次请求中，读取到的配置值都是一样的。

注意： 并不是所有的配置提供器都支持配置重新加载。文件类型的配置器都没有问题，但是环境变量配置器就不可以。

重新加载配置在某些情况下可能很有用，但IOptionsSnapshot还有另一个技巧 - 命名选项(Named Options)。 我们很快就会介绍它们，但首先我们将看一下你可能偶尔遇到的问题，您需要拥有多个设置对象实例。

使用一个强类型配置对象的多个实例

IOption的典型用例就是针对细粒度的配置。配置系统让你很容易的为特定服务注入小的，集中的POCO对象。但是如果你需要配置多个具有相同属性的配置对象时，应该怎么做的？例如，为了将消息发送到Slack, 你需要一个Webhook Url和一个DisplayName. 当你调用SendNotification(message)时，SlackNotificationService会使用这些配置来向指定的Slack Channel中发送消息。

如果你想更新SlackNotificationService以允许你向多个频道发送消息，该怎么办？

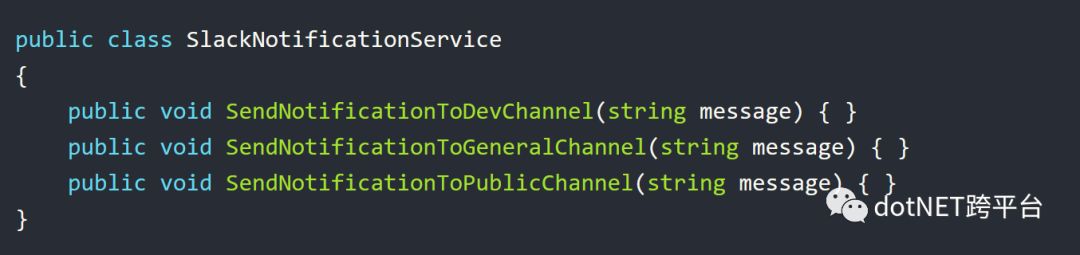
这里我已经为创建了向不同的频道发送消息的方法。但是问题是，我该如何为每个频道配置其对应的Webhook Url和DisplayName。

为了提供一些思路，这里我们假设我们的配置文件结构是这样的。

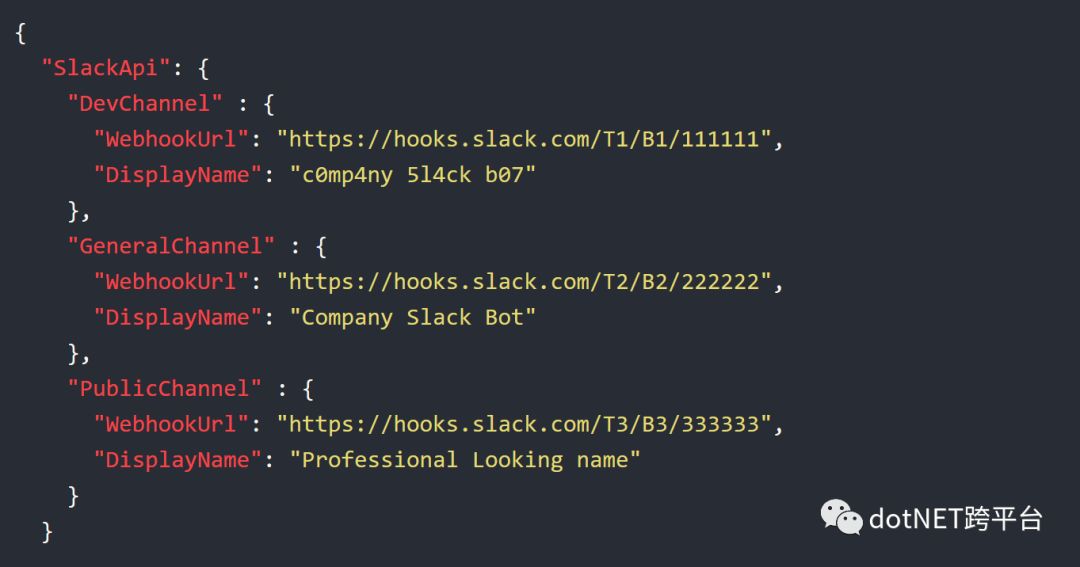
为了在SlackNotificationService中读取到响应的配置，这里有3种可行的方案。

1. 创建父类配置对象

第一种方式就是扩展SlackApiSettings类，在其中包含各个频道的配置属性。

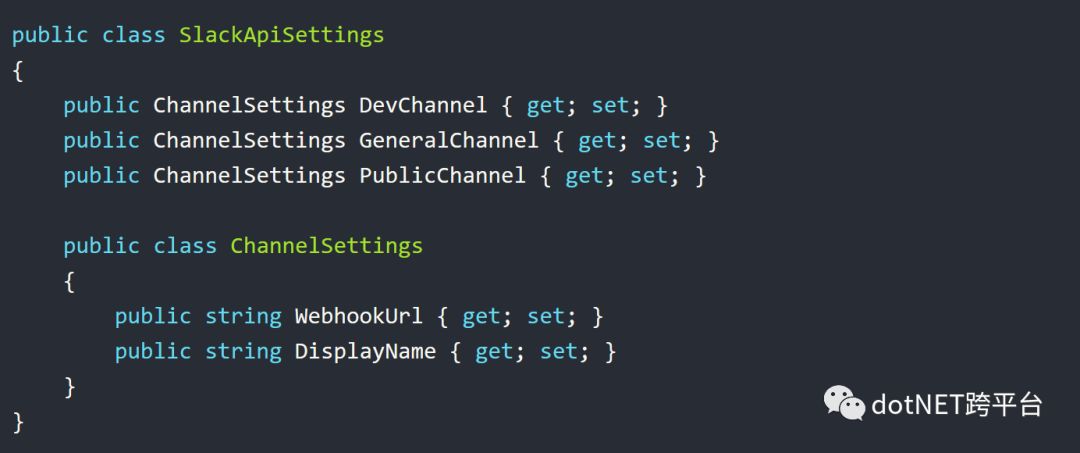
这里我创建了一个内嵌类ChannelSettings, 并在SlackApiSettings类中添加了针对3个Slack Channel的配置。这个新的配置类，正确反映了appSettings.json文件中的配置结构。

在SlackNotificationService中，我们还是和之前一样注入的单个配置类对象

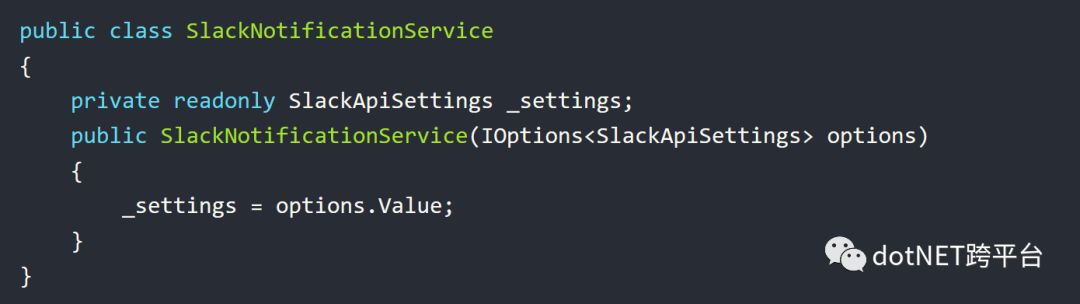
这种配置方式的优点是易于理解，我们为每个Slack Channel配置了独立的强类型配置。缺点是如果要支持新的Slack Channel, 你每次都需要修改SlackApiSettings类。

2. 为每个Channel配置创建单独的配置类

另外一种方法是我们可以独立配置每个Slack Channel。我们分开配置不同的Slack Channel, 并把他们注入到SlackNotificationService服务中。

例如，我们将ChannelSettings类变成一个抽象类

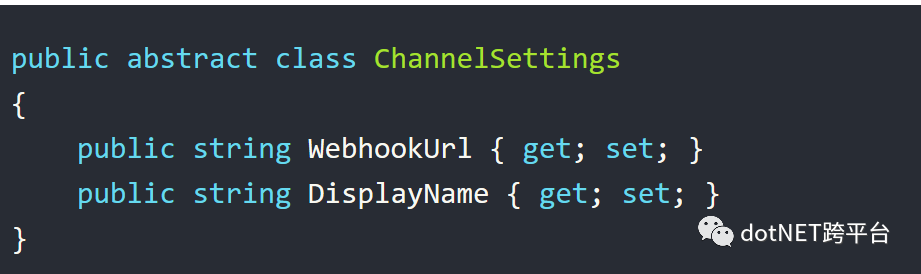
然后每一个Slack Channel的配置类继承ChannelSettings类。

为了配置不同的Slack Channel, 我们需要在程序启动时分别绑定不同的配置节点。

由于不同的Slack Channel拥有不同的配置，所以我们需要分开将他们注入到SlackNotificationService中。

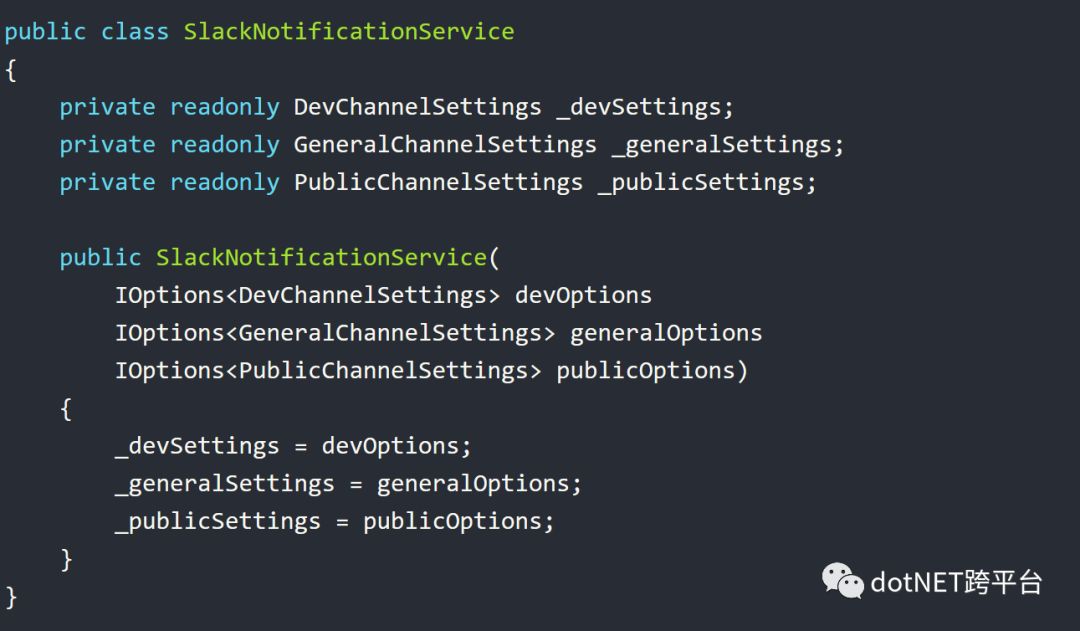
这种方式的好处是当你需要添加新的Slack Channel配置时，你不需要去修改之前定义的配置类结构，你只需要添加一个针对新Slack Channel的配置类。但是它也让事情更加复杂了，你不仅需要为每个新的Slack Channel配置类绑定配置的节点， 还需要修改SlackNotificationService的构造函数添加对新Slack Channel配置类的依赖。

3. 使用Named Options

第三种方案就是本文的主题Named Options。Named Options翻译过来就是命名配置，和它的字面意思一样，我们可以使用它为每个强类型配置对象起一个唯一的名称，并在使用时通过指定唯一名称来获取所需的强类型配置对象。

使用Named Options, 你可以拥有同一个强类型配置类的不同实例，并独立配置他们。这意味着，我们可以继续使用本文开头所定义的SlackApiSettings类。

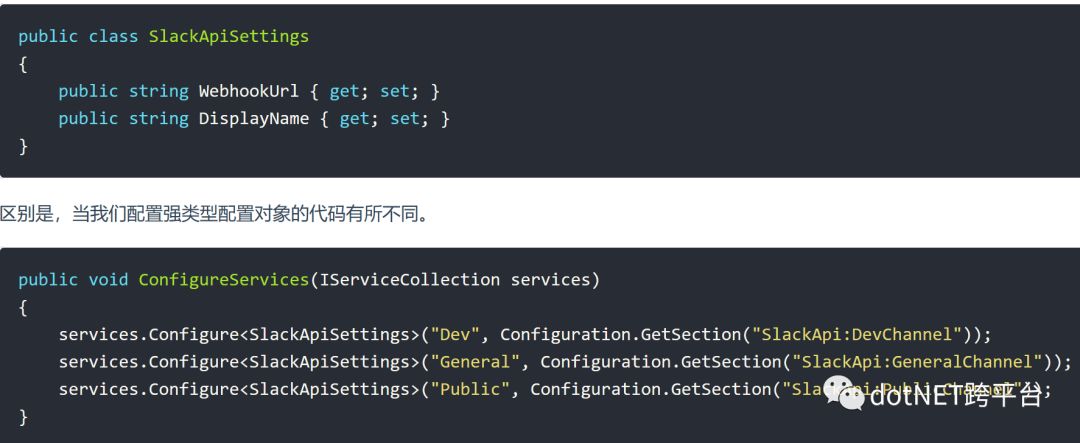
我们使用的Configure的2个参数的重载方法，其中第一个参数指定了一个唯一名称，第二个参数指定了配置文件中对应的节点名称。

为了使用这些命名配置(Named Options), 我们需要在SlackNotificationService类的构造函数中注入IOptionSnapshot对象，而不是我们之前使用的IOption对象。IOptionsSnapshot.Get(name)方法允许我们通过传入唯一名称，获取对应的强类型配置对象。

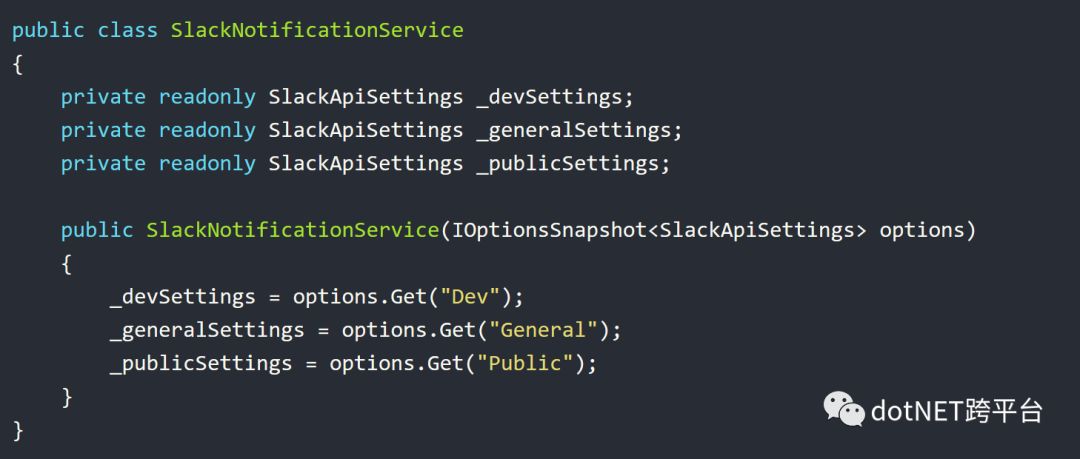
这种方式最大的好处是，当添加新的Slack Channel时，你不需要添加任何新的配置类，你只需要针对新的Slack Channel配置一个新的SlackApiSetting对象即可。缺点是从SlackNotificationService的构造函数上，你已经不知道它对应的配置节点是哪个了。

总结

在本篇博客中，我们介绍了如何在ASP.NET Core中使用强类型配置。然后我们讨论了如何在ASP.NET Core的依赖注入容器中添加强类型配置对象的多个实例。这里我们讲解了使用3种不同的方式

• 创建父类配置对象

• 为每个Channel配置创建单独的配置类

• 使用Named Options

原文地址:https://www.cnblogs.com/lwqlun/p/10133041.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com