一、前言

 　　这几年前端的发展速度就像坐上了火箭，各种的框架一个接一个的出现，需要学习的东西越来越多，分工也越来越细，作为一个 .NET Web 程序猿，多了解了解行业的发展，让自己扩展出新的技能树，对自己的职业发展还是很有帮助的。毕竟，现在都快到9102年了，如果你还是只会 Web Form，或许还是能找到很多的工作机会，可是，这真的不再适应未来的发展了。如果你准备继续在 .NET 平台下进行开发，适时开始拥抱开源，拥抱 ASP.NET Core，即使，现在工作中可能用不到。
　　雪崩发生时，没有一片雪花是无辜的，你也不会知道那片雪花，会引起最后的雪崩。有些自说自话，见谅。

　　系列目录地址：ASP.NET Core 项目实战
　　仓储地址：https://github.com/Lanesra712/Grapefruit.VuCore

 二、Step by Step

　　在整个的开发过程中，后端应用使用 Visual Studio 2017 进行开发，对于前端项目，则是使用 Visual Studio Code 进行开发，嗯，使用专业的工具做相应的事。对于前端的 Vue 项目，我采用的是 Vue CLI 来进行构建的，当然，巨硬也为我们准备了一套 Vue 的模板，如何使用的方法可以在附录中进行查看。

　　1、项目开发环境搭建

　　1.1、安装 .NET Core

　　.NET Core 与之前的 .NET Framework 不一样，它不再紧紧的耦合在 Windows 系统上了，因此，我们可以在支持的操作系统上以安装软件的形式安装我们的 .NET Core 开发环境。

　　打开官网的下载页面（.NET Downloads），找到 .NET Core，这里因为我们需要在当前环境进行开发，所以需要安装 .NET Core SDK，下载完成后，一路 Next 即可。

　　当我们安装完成后，打开控制台，输入命令，则会显示出我们本机安装的 .NET Core 版本。

dotnet --info ## 或者使用 dotnet --version 查看本机安装的 .NET Core 版本信息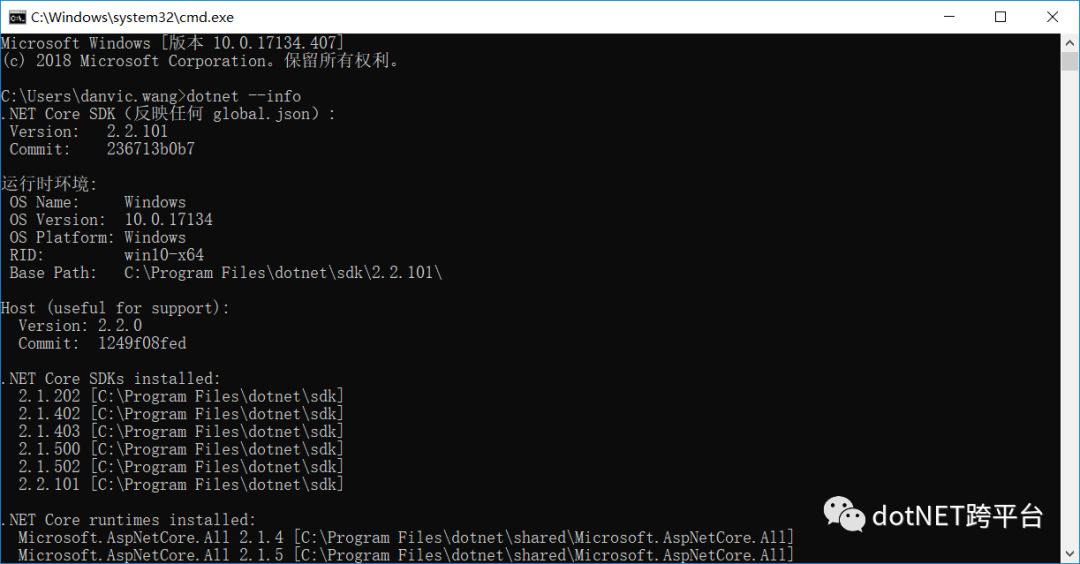

　　在 .NET Core 中为我们提供了 .NET Core CLI 这一工具使我们使用命令行的方式创建我们的 .NET Core 应用，这里我们还是使用 VS 来创建我们的应用，有兴趣的朋友，可以看看园子里的这篇文章 =》.NET Core dotnet 命令大全

　　1.2、安装 Node.js & Vue CLI

　　在整个前后端分离的项目的搭建中，前端的 Vue 项目，是使用 Vue CLI 3 进行搭建的脚手架项目，而 Vue CLI 本质上是一个全局安装的 npm 包，通过安装这一 npm 包可以为我们提供终端里的 vue 命令，因此我们需要使用这一脚手架工具的前提，则是需要我们安装 Node.js 环境。
　　打开 Node.js 官网（Node.js），选择长期支持版下载，之后一路 Next 下去即可。目前的 Node.js 安装包中已经包含了 npm，因此，我们安装好 Node.js 即可。npm 可以类比于我们 .NET 平台的 Nuget，而默认我们安装的全局组件和缓存默认是在 C:\Users\用户名\AppData\Roaming 下，如果你想修改缓存的地址或者全局安装的包地址则需要自己配置环境，具体可参考 =》Node.js安装及环境配置之Windows篇

　　PS：Vue CLI 3 需要 Node.js 8.9 或更高版本 (推荐 8.11.0+)。

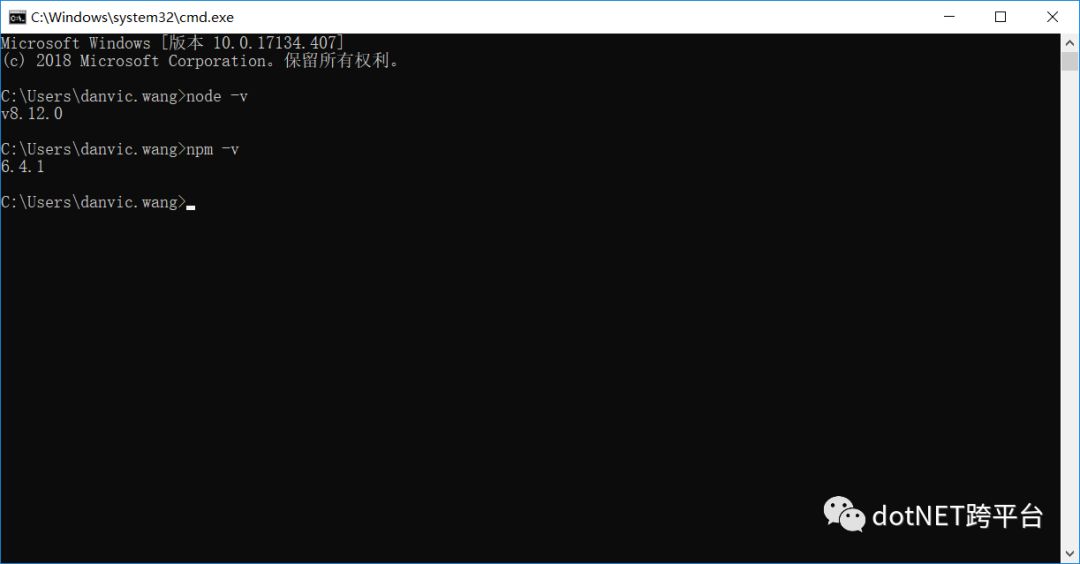
　　当 Node 环境安装好之后，我们就可以安装 Vue CLI 3 脚手架工具了，如果你之前已经全局安装了旧版本的 vue-cli (1.x 或 2.x)，则需要先卸载旧版本的 Vue CLI。

npm uninstall vue-cli -g ## 卸载 vue-cli (1.x or 2.x)
npm install -g @vue/cli

　　安装之后，我们就可以在命令行中使用 vue 命令。

vue ## 查看 vue 相关帮助信息
vue --version ## 查看安装的 vue cli 版本信息

　　1.3、安装 Git

　　为代码添加版本控制是必须的，它可以详细的记录你的每一次操作，以及当你的某次作死导致的环境出错时，你可以很快的恢复环境。经常作死的表示，这个巨需要。
        Git 作为一个分布式的版本控制系统，与 SVN 这种集中式的版本控制系统不同，我们的本地仓库不仅包含了我们的代码，还包含了每个人对代码的操作历史 log，而 SVN 的历史操作记录只存在于中央仓库中。
        这样有什么好处呢？假如，某天中央仓库出错了需要重新创建，因为我们本地的代码不包含操作历史 log，你只能把代码重新放置到中央仓库，而文件的历史版本却丢失了。如果使用 Git 进行版本控制的话，因为我们本地的仓库是一个完整的包含历史操作记录的仓库，我们就可以毫无差别的重新搭建一个中央仓库。
        Git 方面的学习教程，可以看看廖雪峰大神写的这一系列的教程 =》Git 教程
        打开 Git 官网（Git）下载安装包安装，一路 Next 即可。安装完成后，开始菜单里出现 Git Bash 这个应用，则说明我们的 Git 已经安装成功了。安装 Git 之后，我们需要设置我们的名字以及 Email，从而表明我们的身份，这里使用 Git Bash 设置即可。

git config --global user.name "Your Name" ## 全局设置用户名
git config --global user.email "email@example.com" ## 全局设置邮箱

　　2、应用整体框架搭建

　　当我们安装好项目开发的环境之后就可以搭建我们的项目框架了，这里我选择将前后端的项目放到同一个 Git 仓储中，你也可以根据你自己的喜好放到多个 Git 仓储中。
　　新建一个文件夹作为仓储，在创建好的文件夹路径下打开 Git Bash，初始化我们的仓储。如果你勾选了显示隐藏文件夹，则会发现，当我们执行好初始化的命令之后，则会在当前文件夹下创建一个 .git 文件夹。

git init

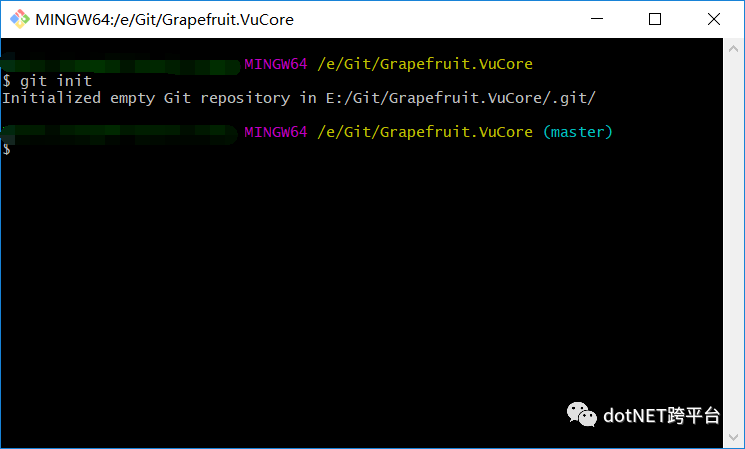
　　当然，你也可以使用 VS 进行创建 Git 仓储，使用 VS 创建仓储后会自动帮我们创建 .gitignore 和 .gitattributes 文件，同样的，后续对于该仓储的任何 Git 操作，我们也可以通过 VS 进行。
　　gitignore 文件表示我们需要忽略的文件或目录，而 gitattribute 则用于设置非文本文件的对比方式，这里我们使用 VS 创建 Git 仓储后生成的 gitignore 文件默认会添加 .NET 项目需要忽略提交的文件和目录。因为，前端的项目我是使用 VS Code 进行开发的，这里，我需要将一些 VS Code 生成的文件也添加到 gitignore 文件中。

.vscode/*!.vscode/settings.json
!.vscode/tasks.json
!.vscode/launch.json
!.vscode/extensions.json

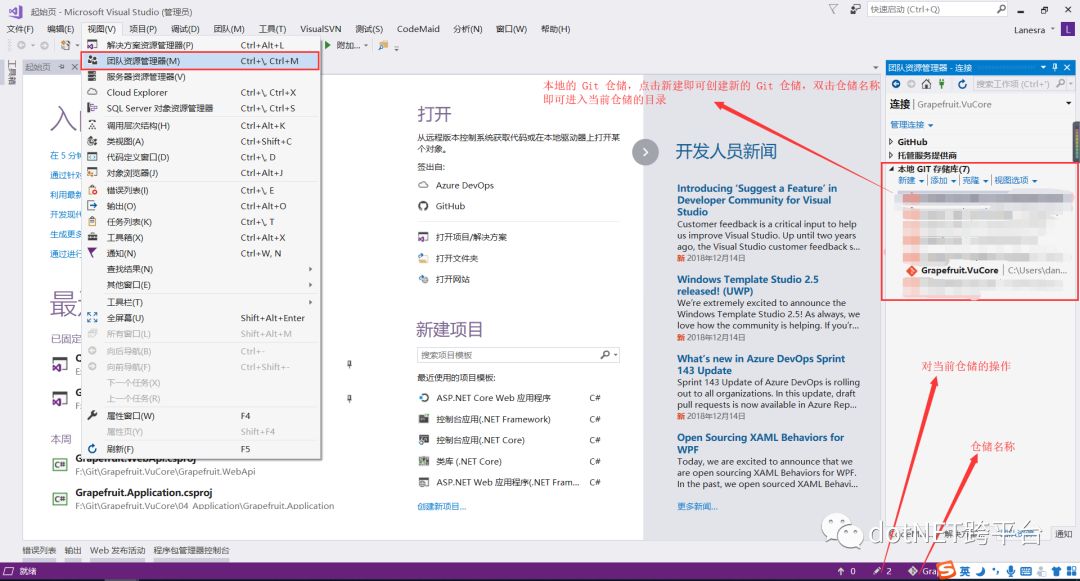
　　创建 ASP.NET Core Web API 的具体过程就不演示了，这里采用的就是基础的多层架构，当我们创建好项目之后，可以看到 VS 右下角铅笔 icon 处会显示我们未做提交的修改。点击 icon ，输入我们的提交信息后，就可以将我们的修改提交到仓储中。

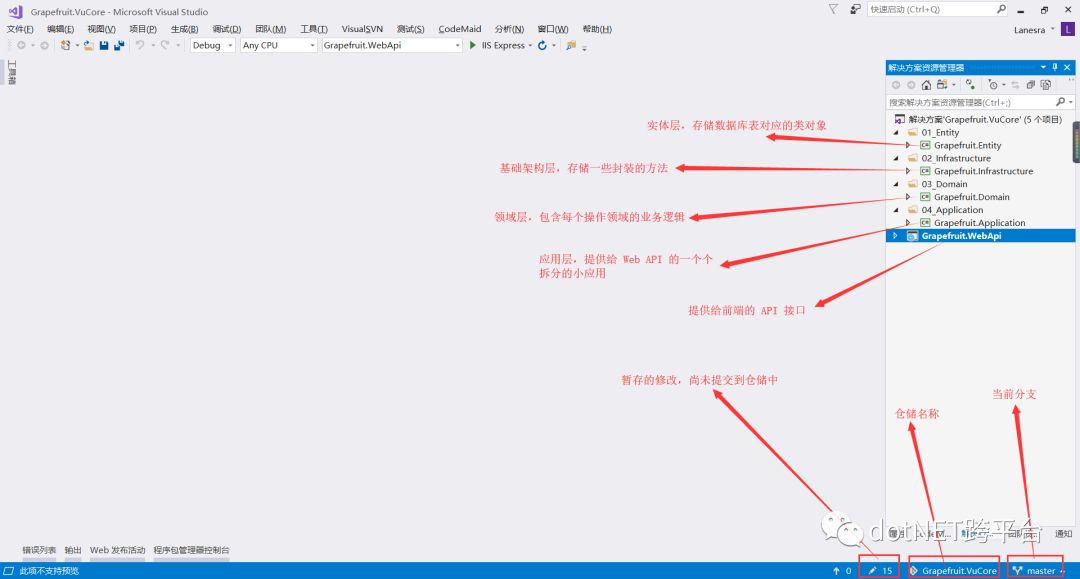
　　后端的 API 接口应用创建好了，现在我们使用 Vue CLI 来构建我们前端的 Vue 项目。这里，我选择在解决方案的根目录创建我们的前端项目。
　　在 Vue CLI 3 中，我们不仅可以使用 vue create 命令来创建我们的项目，而且可以使用图形化的页面创建我们的应用。

vue create project-name ## 使用命令行的形式创建
vue ui ## 使用图形化的方式创建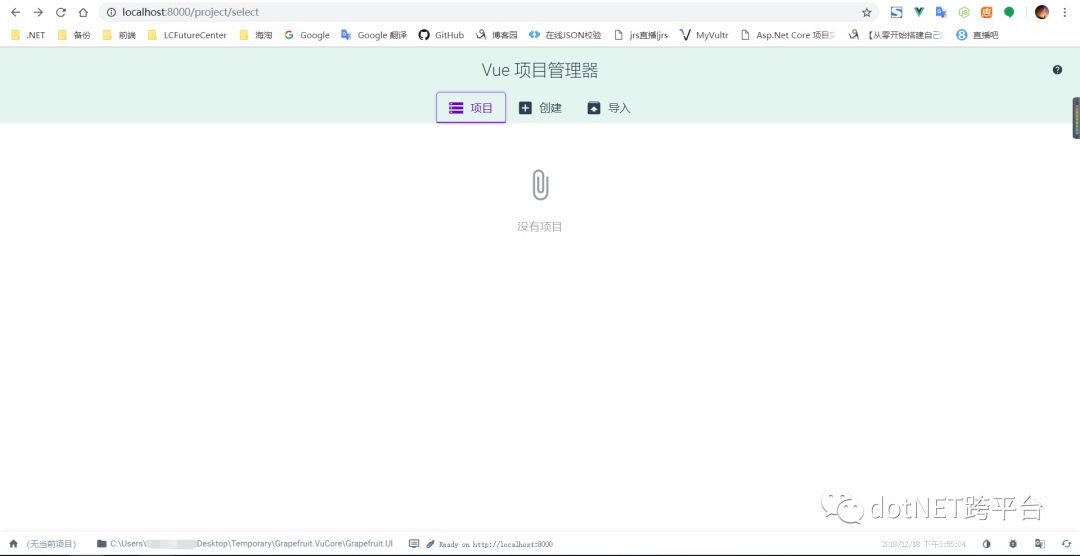

　　

　　当使用 vue ui 命令后会自动打开创建项目的页面，可以看到，这个路径下，并没有创建好的项目，你可以选择从别的路径下导入，或者是直接创建新的项目。如果你有使用过 Vue CLI 之前的版本，使用大写字母创建项目时是会报错的，但是在 Vue CLI 3 版本中没有出现这种问题。

　　因为我将前端项目与后端的项目放到同一个仓储中，所以这里就不需要再进行初始化 git 仓库了，对于项目的配置，这里就采用默认的配置。点击创建之后就会自动搭建我们的项目。如何启动这个脚手架项目，可以按照生成的 README 文件中的步骤执行。

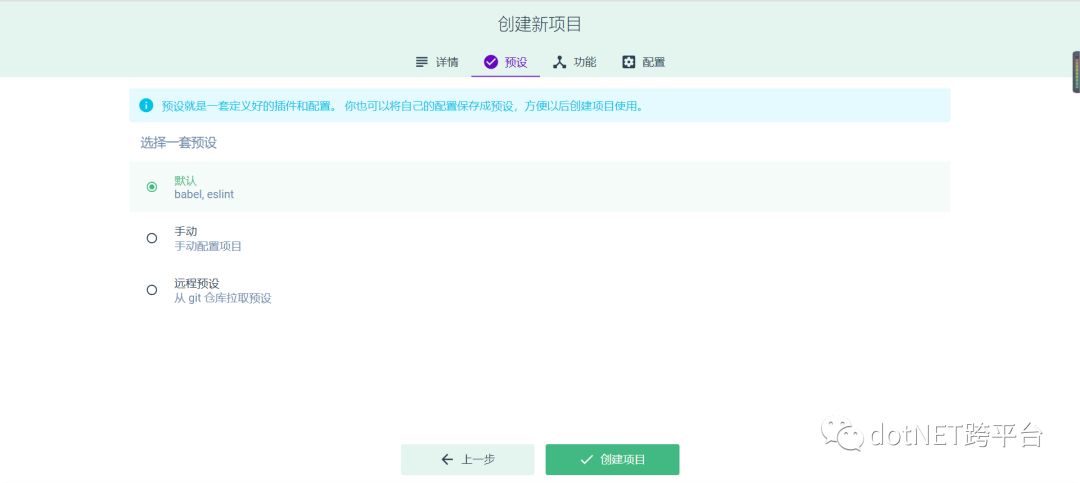
　　到这里，基础的 Vue 脚手架项目就已经搭建完成了，对于添加插件之类的内容，放到我们后面的内容中。另外，虽然我们在创建项目时并没有勾选初始化 Git 仓储，但是 Vue CLI 还是创建了一个 gitignore 文件，如果你和我一样，是将前后端项目放到一个仓储的话，可以把这个文件里的内容复制到项目根目录中的 gitignore 文件中，然后把这个文件删除。

 三、附录

 　　微软官方有提供一套 Vue 的 SPA 应用模板，不过并没有显示在我们使用 VS 创建项目的页面中，而且需要我们添加一个插件之后，使用 .NET Core CLI 的方式创建。因为自己并没有详细了解这块的内容，这里只列出创建的方法，详细的介绍请查看微软的官方文档（Building Single Page Applications on ASP.NET Core with JavaScriptServices ）。

## 安装 SPA 模板
dotnet new --install Microsoft.AspNetCore.SpaTemplates::*

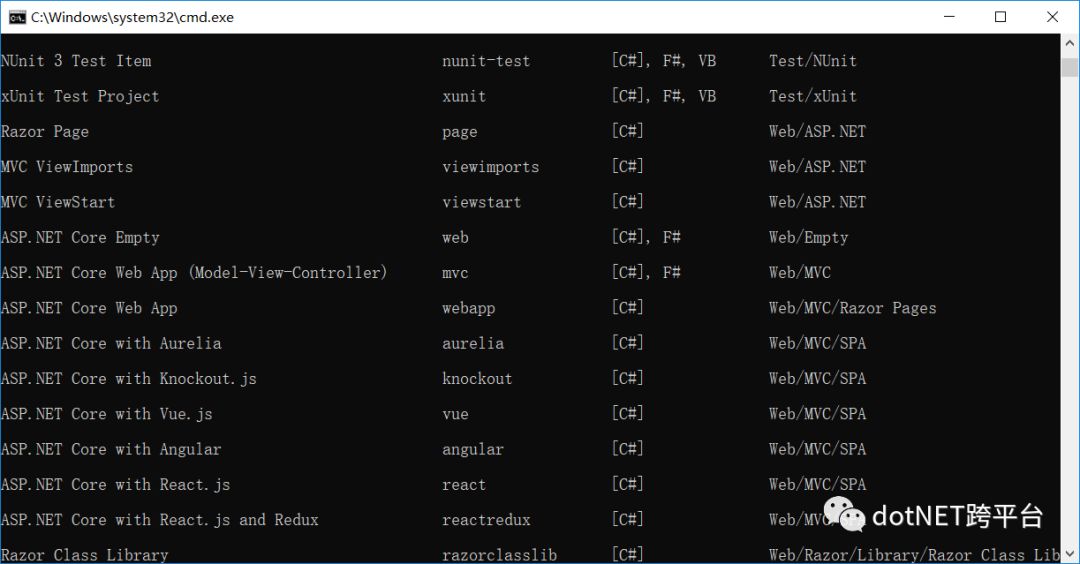
　　当你安装好模板之后，可以看到，多了使用 Aurelia、Vue、Knockout 创建 SPA 模板的选项，这时我们就可以使用 dotnet new 命令来创建包含 Vue 的模板应用。模板创建完成后需要安装依赖的包。加载完依赖的包之后，我们就可以通过 VS 或 VS Code 开发调试我们的项目。

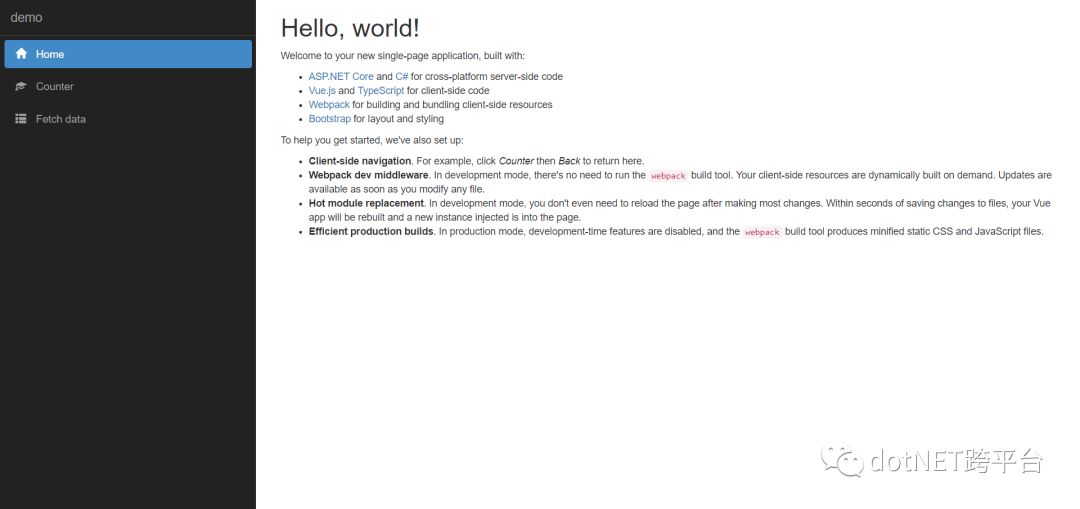
dotnet new vue ## 创建 Vue SPA 项目
npm install ## 还原依赖的 npm 包

 四、总结

 　　这一章没有包含很多的内容，主要就是如何搭建我们的 .NET Core 和 Vue 的开发环境，以及创建我们的项目架构，在后面的文章中则会慢慢的阐述整个项目的开发过程，希望可以能对你有一丢丢的帮助。