题目描述

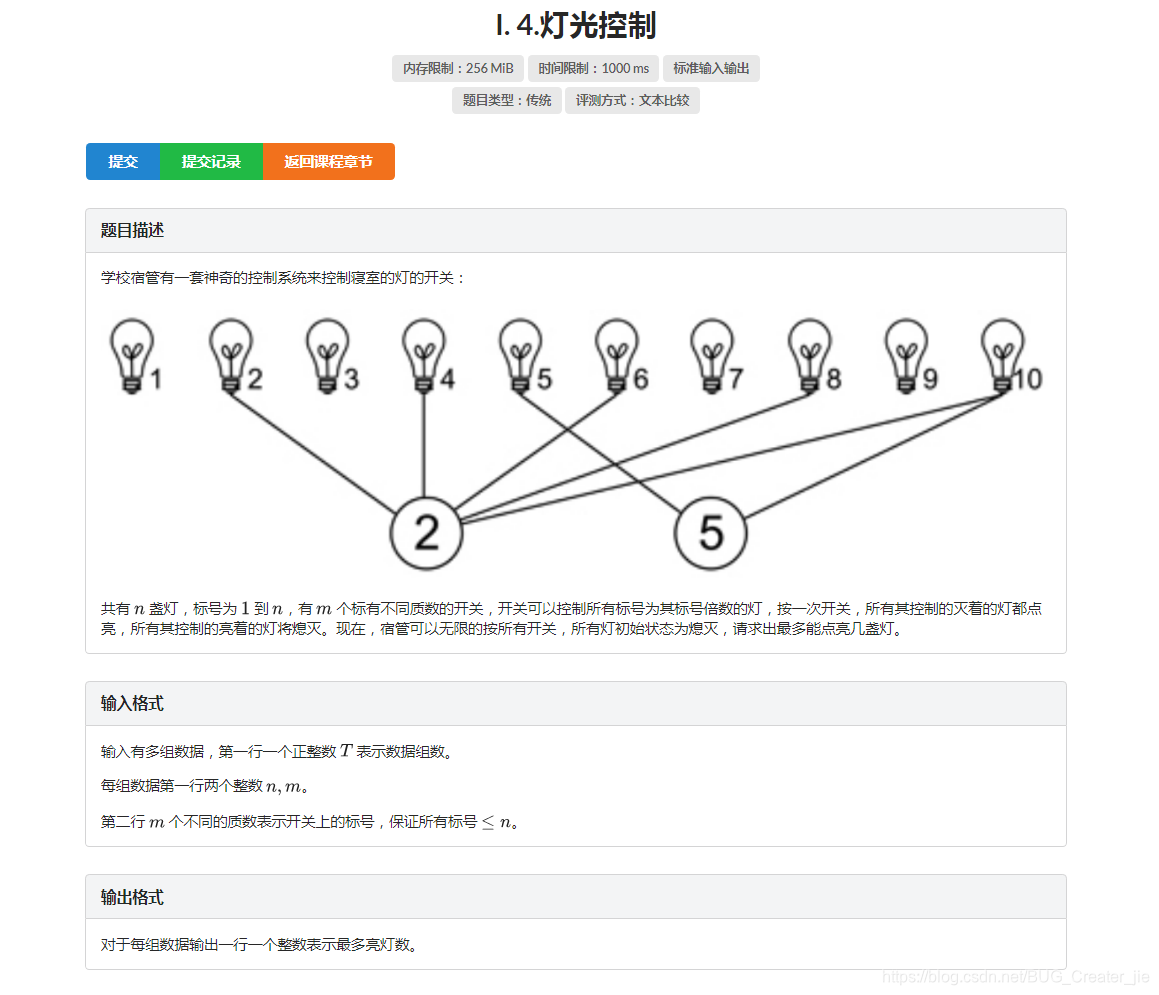
解析

没有想出来
首先可以确定开关要么开一次，要么不动，其他都和这俩是等价的
一开始最先想到的就是贪心的方法，每个开关遍历，如果按下会使答案变好就按下。
但是显然当前的开闭对后面是有后效性的，很容易就hack掉了
于是，我的思维就去了其他的天涯海角…
在正解的门前回了头
qwq
因为都是质数，所以假设两个开关x和y，它们一定互质
那么它们会互相影响的（也就是公倍数），一定是X*Y的整数倍
（讽刺的是这个我也发现了，就差拼在一起）
那么我们就可以发现：
对于所以大于根号n的开关，它们互相之间是不会互相影响的！
这是本题的关键性质
那么，我们如果确定了<=根号n的开关的状态，后面的开关就可以使用贪心解决了
而我们又发现：<=根号n的质数非常至少，最多只有11个
dfs暴力枚举所有可能状态即可
问题得到解决

代码

#include<bits/stdc++.h>
#define ll long long
//#define int long long
using namespace std;
const int N=1050;
const int M=1e6;
const int mod=1e9+7;
int a[N],na,b[N],nb;
int n,t,m,ans;
int q[N];
int x[N];
void dfs(int k){if(k>na){for(int i=1;i<=n;i++) x[i]=0;for(int i=1;i<=na;i++){if(!q[i]) continue;int now=a[i];for(int j=now;j<=n;j+=now) x[j]^=1;}int tot=0;//printf("k=%d\n",k);for(int i=1;i<=n;i++) tot+=x[i];for(int i=1;i<=nb;i++){int now=b[i],val=0;for(int j=now;j<=n;j+=now){val += x[j]==0 ? 1 : -1;}if(val>0) {tot+=val;for(int j=now;j<=n;j+=now) x[j]^=1;}}ans=max(ans,tot);return;}q[k]=1;dfs(k+1);q[k]=0;dfs(k+1);
}
int main() {scanf("%d",&t);while(t--){scanf("%d%d",&n,&m);ans=0;na=0;nb=0;for(int i=1;i<=m;i++){int o;scanf("%d",&o);if(o<floor(sqrt(n)))	a[++na]=o;else b[++nb]=o;}dfs(1);printf("%d\n",ans);}return 0;
}/*		
4
10 2
2 5
21 4
2 3 5 7
100 1
5
100 3
3 19 7
*/