二维单调队列模板

E题是一个二维单调队列的板题，这里就先把板子甩出来
二维板子就是先维护每行，每行都是一个单调队列，然后再用行去维护列
求n*m矩阵中，边长为k的每个矩阵的最大值：
维护的行的最大值模板：

void solve_row () {for ( int i = 1;i <= n;i ++ ) {int head = 1, tail = 0;for ( int j = 1;j <= m + 1;j ++ ) {if ( j >= k + 1 ) {while ( head <= tail && deq[head] < j - k )head ++;rowmax[i][j - k] = h[i][deq[head]];}while ( head <= tail && h[i][deq[tail]] <= h[i][j] )tail --;deq[++ tail] = j;}}
}

维护列的最大值的模板

void solve_col () {for ( int j = 1;j <= m;j ++ ) {int head = 1, tail = 0;for ( int i = 1;i <= n + 1;i ++ ) {if ( i >= k + 1 ) {while ( head <= tail && deq[head] < i - k )head ++;colmax[i][j] = rowmax[deq[head]][j];}while ( head <= tail && rowmax[deq[tail]][j] <= rowmax[i][j] )tail --;deq[++ tail] = i;}}
}

输出模板：

for ( int i = 1;i <= n - k + 1;i ++ ) {for ( int j = 1;j <= m - k + 1;j ++ )printf ( "%d ", colmax[i][j] );printf ( "\n" );
}

维护行的最小值的模板

void solve_row () {for ( int i = 1;i <= n;i ++ ) {int head = 1, tail = 0;for ( int j = 1;j <= m + 1;j ++ ) {if ( j >= k + 1 ) {while ( head <= tail && deq[head] < j - k )head ++;rowmin[i][j - k] = h[i][deq[head]];}while ( head <= tail && h[i][deq[tail]] >= h[i][j] )tail --;deq[++ tail] = j;}}
}

维护列的最小值的模板

void solve_col () {for ( int j = 1;j <= m;j ++ ) {int head = 1, tail = 0;for ( int i = 1;i <= n + 1;i ++ ) {if ( i >= k + 1 ) {while ( head <= tail && deq[head] < i - k )head ++;colmin[i][j] = rowmin[deq[head]][j];}while ( head <= tail && rowmin[deq[tail]][j] >= rowmin[i][j] )tail --;deq[++ tail] = i;}}
}

输出模板

for ( int i = 1;i <= n - k + 1;i ++ ) {for ( int j = 1;j <= m - k + 1;j ++ )printf ( "%d ", colmin[i][j] );printf ( "\n" );
}

六神装已经出完，开始我们的三杀之旅吧！我要carry全场！

C：Basketball Exercise

题目大意

输入n接下来输入两个长度为n的h1，h2序列
然后开始从1~n进行选取，当在i位置的时候
1）不选，跳过
2）如果上一次的选择是h1数组，这一次就只能选h2[i]
3）如果上一次选的是h2序列，这一次就只能选h1[i]
求最后选取的数的和的最大值
n (1≤n≤10^5)
(1≤h2i，h1i≤10^9)

【输入输出样例】
Input
5
9 3 5 7 3
5 8 1 4 5
Output
29
Input
3
1 2 9
10 1 1
Output
19
Input
1
7
4
Output
7
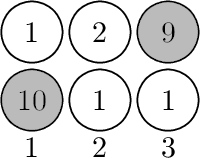
【样例解释】
灰色是选的点
样例1：
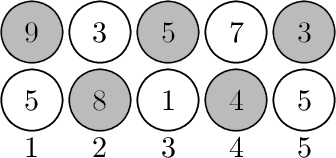
在这里插入图片描述
样例2：

题解

i点有三种情况，不选，或根据前一个操作决定是选h1还是h2
那么i与前面挂钩，肯定可以搜索，数据范围又大，搜索会炸
坑定就是dp啦，况且本仙女最差的就是dp这玩意，我都能一眼看出这是dp
你说这道题板不版！
dp式也很简单我们定义一个二维就行，第一维表示模拟序列中i的位置，第二维三种状态
0表示不选i，1表示上一次选的h2，2表示上一次选的h1

好了，上马

代码实现

#include <cstdio>
#include <iostream>
using namespace std;
#define MAXN 100005
#define LL long long
int n;
int a[MAXN], b[MAXN];
LL dp[MAXN][3];
LL result;
int main() {scanf ( "%d", &n );for ( int i = 1;i <= n;i ++ )scanf ( "%d", &a[i] );for ( int i = 1;i <= n;i ++ )scanf ( "%d", &b[i] );for ( int i = 1;i <= n;i ++ ) {dp[i][0] = max ( dp[i - 1][1], dp[i - 1][2] );dp[i][1] = max ( dp[i - 1][0], dp[i - 1][2] ) + a[i];dp[i][2] = max ( dp[i - 1][0], dp[i - 1][1] ) + b[i];}printf ( "%lld", max ( dp[n][1], dp[n][2] ) );return 0;
}

D2：Submarine in the Rybinsk Sea (hard edition)

ex至极，这tmd的mod就这么喜欢我吗，我这几天已经被它搞了3次了
你成全我吧！我们之间是没有结果的，你是单箭头，我已经把心交给了学习！
在这里插入图片描述

题目大意

输入n然后n个数，每两个数进行组合成一个新的数
如果第一个数位数大于第二个数的位数，第一个位数的前面不动，然后第一个数选一个，第二个数选一个。eg：91234，567，那么它们进行匹配的结果就是91253647
如果第二个数位大于第一个的数位，第二个位数的前面不动，还是第一个数选一个，第二个数选一个。eg：7658，123490，那么它们进行组合的结果就是1273645980

而且每两个数能组合成两个新数，因为这两个数都可以分别成为第一个数
eg：1234，5678组合的新数分别是15263748和51627384

他也可以和自己组合，eg：23它与自己组合就是2233，不过这个数只统计一次
而如果是不同的i，j但是他们都是23，2233就要算两次

求最后组合的所有新数的和取模998244353

n (1≤n≤100000)(1≤ai≤10^9)

题解

首先要知道两个ai如果都是1e9就必须要开longlong

接着我们来思考如果i的位数小于等于j的位数
那么i对i，j进行组合后的新数的贡献是一定的
eg：23，156组合后：12536，15263
23的个位对这些新数的贡献和为3在十位和个位的和，即33
23的十位对这些新数的贡献和为2在百位和千位的和，即2200
总贡献就是2233

如果i的位数大于j的位数
就用上面的例子来说明
156的个位和十位算法与上面一致
而从它多的位数开始的时候，它在新数的位置是固定的
不过有两个新数，那么156的百位的贡献就是两个10000，即20000

接下来用这种公式，就算位数为j的数字个数>2，直接乘以tot个数就行了
一定要注意mod，多mod又不会出事反正没有除法是吧！模模益善！

终于可以上车了！把车门给我焊死
在这里插入图片描述

代码实现

我写得有点多，mod模的很多，主要是害怕炸longlong，结果后面还是炸到了cs
如果是位数大于等于a[i]
cs就是模拟的a[i]的第j位会对答案做出哪两位的贡献，比如模拟的是个位那么我就用cs算出他在十位和个位的总贡献
如果是位数小于a[i]
cs还可以模拟固定的j位，比如23和145，cs就能模拟出1的贡献是200

#include <cstdio>
#define LL long long
#define mod 998244353
#define MAXN 100005
LL n;
LL a[MAXN];
LL tot[MAXN];
LL wei[MAXN];
LL result;
int main() {scanf ( "%lld", &n );for ( int i = 1;i <= n;i ++ ) {scanf ( "%lld", &a[i] );LL tmp = a[i];int cnt = 0;while ( tmp ) {cnt ++;tmp /= 10;}wei[i] = cnt;tot[cnt] ++;}for ( int i = 1;i <= n;i ++ ) {for ( int j = 1;j < wei[i];j ++ ) {if ( tot[j] == 0 ) continue;LL x = a[i], cs = 1, many = 1, t;while ( x ) {cs %= mod;t = x % 10;if ( many <= j ) result = ( result + ( t * cs % mod + cs * 10 % mod * t % mod ) % mod * tot[j] % mod ) % mod;elseresult = ( result + tot[j] * 2 % mod * t % mod * cs % mod ) % mod;x /= 10;if ( many <= j ) cs *= 100;else cs *= 10; many ++;}}for ( int j = wei[i];j <= 10;j ++ ) {if ( tot[j] == 0 ) continue;LL x = a[i], cs = 1, t;while ( x ) {cs %= mod;t = x % 10;result = ( result + ( t * cs % mod + cs * 10 % mod * t % mod ) % mod * tot[j] % mod ) % mod;x /= 10;cs *= 100;}}}printf ( "%lld", result % mod );return 0;
}

E：OpenStreetMap

题目大意

输入n，m，a，b
再输入g0，x，y，z
g[i]=(g[i−1] ⋅ x + y) mod z
hi,j=g[(i−1)⋅m+j−1]
求在行n列m的h矩阵中，所有a*b矩阵中最小值的和
(1≤n,m≤3000, 1≤a≤n, 1≤b≤m)(0≤g0,x,y<z≤10^9)

题解

所有a*b矩阵就很像一个滑动窗口再加上是求最值，那坑定就是用单调队列来维护
不过是个二维的滑动窗口罢了。。。我没有想说的了

在代码中我没有用c数组来记录维护的列的最小值，因为就多这一个二维数组，我就MLE
所以我在维护列的时候就顺便吧答案也给求了！
在这里插入图片描述
话不多说，屁不多放，上马

代码实现

#include <cstdio>
#include <iostream>
using namespace std;
#define LL long long
#define MAXN 3005
LL n, m, a, b, ii, x, y, z;
LL sum;
LL g[MAXN * MAXN], h[MAXN][MAXN];
LL row[MAXN][MAXN];
LL deq[MAXN];void init () {g[0] = ii;for ( int i = 1;i <= ( n - 1 ) * m + m - 1;i ++ )g[i] = ( g[i - 1] * x + y ) % z;for ( int i = 1;i <= n;i ++ )for ( int j = 1;j <= m;j ++ )h[i][j] = g[( i - 1 ) * m + j - 1];
}void solve_row () {for ( int i = 1;i <= n;i ++ ) {int head = 1, tail = 0;for ( int j = 1;j <= m + 1;j ++ ) {if ( j >= b + 1 ) {while ( head <= tail && deq[head] < j - b )head ++;row[i][j - b] = h[i][deq[head]];}while ( head <= tail && h[i][deq[tail]] >= h[i][j] )tail --;deq[++ tail] = j;}}
}
void solve_col () {for ( int j = 1;j <= m;j ++ ) {int head = 1, tail = 0;for ( int i = 1;i <= n + 1;i ++ ) {if ( i >= a + 1 ) {while ( head <= tail && deq[head] < i - a )head ++;sum += row[deq[head]][j];}while ( head <= tail && row[deq[tail]][j] >= row[i][j] )tail --;deq[++ tail] = i;}}
}int main() {scanf ( "%lld %lld %lld %lld", &n, &m, &a, &b );scanf ( "%lld %lld %lld %lld", &ii, &x, &y, &z );init ();solve_row ();solve_col ();printf ( "%lld", sum );return 0;
}