题目描述

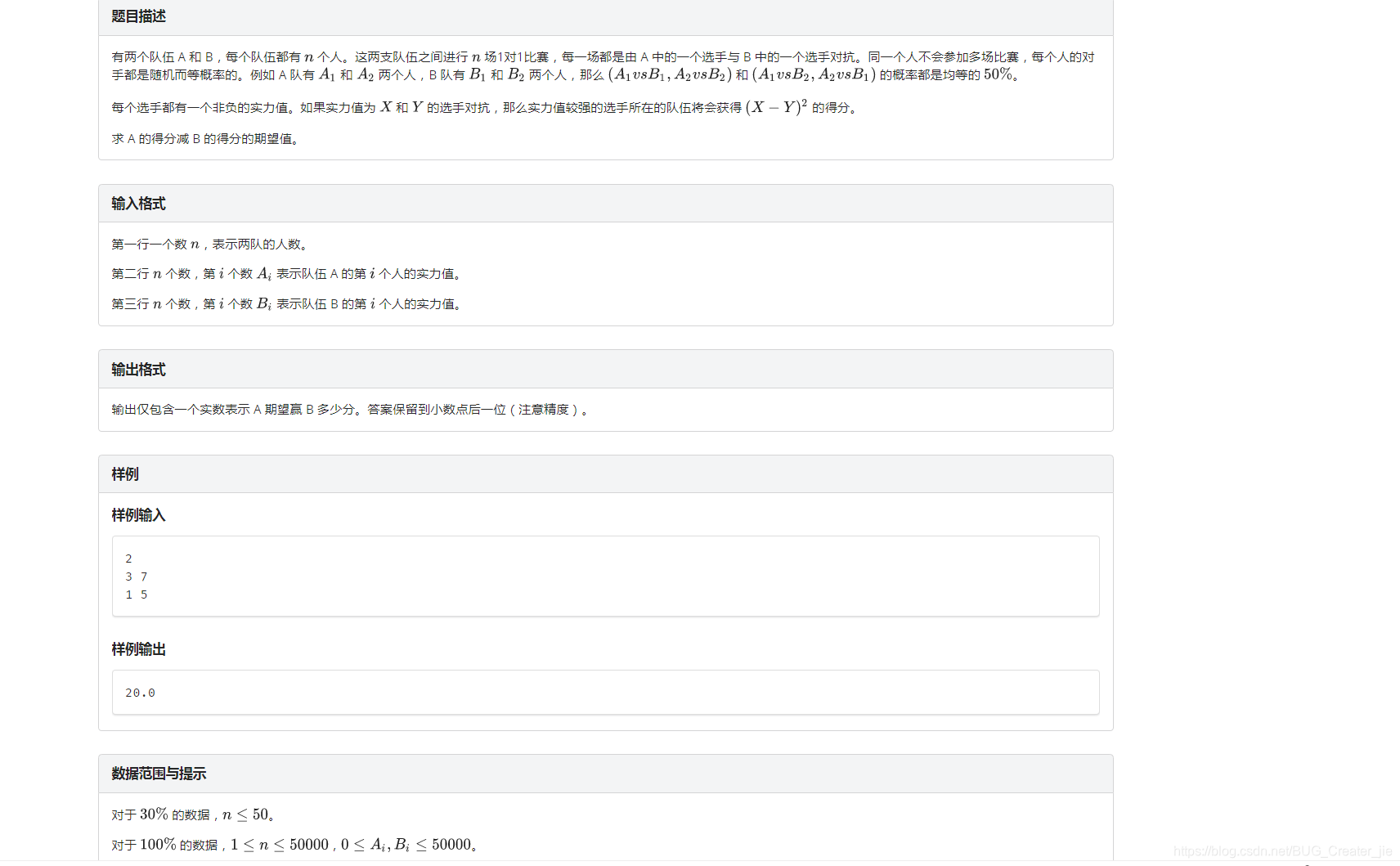
解析

不太难的题
显然本题在AB队员大小关系相反时其对答案的贡献互为相反数。
所以想到把B队队员sort一下后就可以二分找到大小关系相反的分界点
然后维护和与平方和两个前缀数组搞一搞即可O1求出贡献
总复杂度：$nlogn$
但是一开始卡精度卡掉了9分！后来经试验发现：

ans += 1.0 * (pl * x[i] * x[i] + p[pl] - 2 * x[i] * sum[pl]);
ans -= 1.0 * ((n - pl) * x[i] * x[i] + (p[n] - p[pl]) - 2 * x[i] * (sum[n] - sum[pl]));

这么算有一个点会差0.1
但是，如果合并一下，写成——

ans+=1.0*((2*pl-n)*x[i]*x[i]+2*p[pl]-p[n]-2*x[i]*(2*sum[pl]-sum[n]))/n;

就能AC了
到底为什么我也不太明白
希望有识之士能教教我qwq
（评论私聊均可啊！）

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+100;
const int mod=1e6;
int n,m,k;
double x[N],y[N];
double sum[N],p[N];
int main(){scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%lf",&x[i]);for(int i=1;i<=n;i++) scanf("%lf",&y[i]);sort(y+1,y+1+n);for(int i=1;i<=n;i++){sum[i]=sum[i-1]+y[i];p[i]=p[i-1]+y[i]*y[i];}double ans=0;for(int i=1;i<=n;i++){int pl=upper_bound(y+1,y+1+n,x[i])-y;pl--;ans+=1.0*((2*pl-n)*x[i]*x[i]+2*p[pl]-p[n]-2*x[i]*(2*sum[pl]-sum[n]))/n;//ans-=1.0*((n-pl)*x[i]*x[i]+(p[n]-p[pl])-2*x[i]*(sum[n]-sum[pl]))/n;}printf("%.1lf\n",ans);return 0;
}