DncZeus

前言

关于 DncZeus

DncZeus = Dnc + Zeus

"Dnc"--.Net Core 的缩写；

"Zeus"--中文译为宙斯，是古希腊神话中的众神之王，奥林匹斯十二主神之首，统治宇宙万物的至高无上的主神（在古希腊神话中主神专指宙斯），人们常用“众神和人类的父亲”、“神王”来称呼他，是希腊神话诸神中最伟大的神。

DncZeus的愿景就是做一个.NET Core 领域的简易精致的通用后台权限管理模板系统基础框架，努力向.NET Core 领域的"宙斯"看齐。

项目简介

DncZeus是一个基于 ASP.NET Core 2 + Vue.js 的前后端分离的通用后台管理系统框架。后端使用.NET Core 2 + Entity Framework Core 构建，UI 则是目前流行的基于 Vue.js 的 iView。项目实现了前后端的动态权限管理和控制以及基于 JWT 的用户令牌认证机制，让前后端的交互更流畅。

DncZeus并不是一个完整的业务系统，但她提供完成业务系统的绝大多数开发场景，让每一位.NET 开发者都能基于DncZeus快速开发出交互、体验以及功能具佳的.NET Core 单页应用程序(SPA)。

支持DncZeus(求Start :))

如果你觉得DncZeus对你或者他人有用，请为DncZeus点个赞，求扩散，让更多人获得帮助！！！

开源地址

超级管理员：administrator
管理员：admin

密码：111111

地址：https://github.com/lampo1024/DncZeus

由于是个人项目，资金有限，体验服是低配，请大家爱惜，轻戳，不胜感激！！！

适合人群

由于 DncZeus 考虑到初级.NET 开发者都可以使用，所以后端项目未涉及过多架构和封装(代码逻辑一目了然)，但为了你更好地熟悉和运用 DncZeus，你需要了解：

• ASP.NET Core

• Vue.js

• iView

ASP.NET Core 的知识能确保你可以看懂和了解后端是如何实现和工作的，而 Vue.js 框架则是前端实现的基石，当然 iView 这个基于 Vue.js 的 UI 框架也是必须要了解的，因为 DncZeus 正是基于 iview-admin(iView 的一个后台管理系统示例项目)来实现的前端 UI 交互。

如果你对这两个方面的知识还不熟悉，建议你可以先学习一些理论再来运用 DncZeus 这个框架。关于 ASP.NET Core 和 Vue.js 的入门请参考：

• ASP.NET Core 官方文档

• Vue.js 官方文档

环境和工具

1. Node.js(同时安装 npm 前端包管理工具)

2. Visual Studio 2017(15.8.8 或者以上版本)

3. VS Code 或者其他前端开发工具

4. git 管理工具

5. SQL Server CE 或者 SQL Server Express 或者 SQL Server 2014 +

技术实现

• ASP.NET Core 2(.NET Core 2.1.502)

• ASP.NET WebApi Core

• JWT 令牌认证

• AutoMapper

• Entity Framework Core 2.0

• .NET Core 依赖注入

• Swagger UI

• Vue.js(ES6 语法)

• iView(基于 Vue.js 的 UI 框架)

下载项目

使用Git工具下载

首先请确保你本地开发环境已安装了git管理工具，然后在需要存放本项目的目录打开git命令行工具Git Bash Here，在命令行中输入如下命令：

git clone https://github.com/lampo1024/DncZeus.git

以上命令就把DncZeus的远程代码拉取到你的本地开发机上。

手动下载

如果你不愿意使用git管理工具下载DncZeus的远程代码，你也可以在github托管地址手动下载，打开地址https://github.com/lampo1024/DncZeus，找到页面中的按钮"Clone or download"，如下图示：

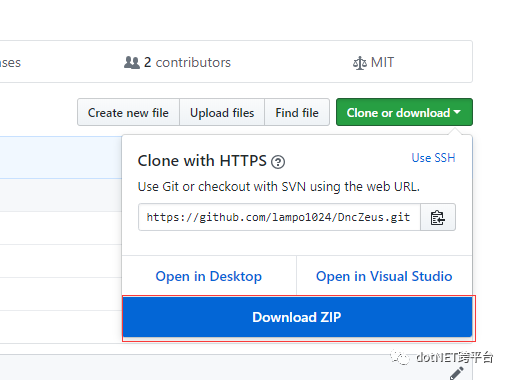
在弹出的对话框中点击按钮"Download ZIP"即可开始下载DncZeus的源代码，如下图：

安装依赖

前端项目

在将DncZeus的源代码下载到本地之后，如果你使用的git管理工具，可以不用退出当前的git管理工具，输入如下命令：

cd DncZeus/DncZeus.App

进入到DncZeus的前端项目目录DncZeus.App。在命令行中输入如下命令进行前端依赖包的还原操作：

npm install

或者

npm i

后端项目

在Visual Studio中打开解决方案[DncZeus.sln]。首先根据自己的开发环境(SQL Server数据库类型，本示例默认是SQL Server Localdb)修改配置文件appsettings.json中的数据库连接字符串，示例默认连接字符串为：

"ConnectionStrings": {    "DefaultConnection": "Server=(localdb)\\mssqllocaldb;Database=DncZeus;Trusted_Connection=True;MultipleActiveResultSets=true"}

再打开包管理控制台(Package Manager Console)，执行如下命令生成数据库表结构：

Update-Database -verbose

最后，打开项目根目录中的脚本文件夹[Scripts]，执行脚本文件[Init_data.sql]以初始化系统数据。

恭喜你，到这里所有的准备工作就完成了。

赶紧体验DncZeus框架吧！！！

运行

1. 使用Visual Studio开发工具打开DncZeus根目录中的VS解决方案文件DncZeus.sln，设置DncZeus.Api项目为默认启动项并运行此项目。

这时在浏览器中打开地址：http://localhost:54321/swagger ，便可以查看到DncZeus已经实现的后端API接口服务了。

1. 在命令行中进入到DncZeus的前端项目目录[DncZeus.App]，运行如下命令以启动前端项目服务：

npm run dev

成功运行后会自动在浏览器中打开地址: http://localhost:9000

使用和授权

DncZeus项目是一个开源项目，你可以直接基于本项目进行扩展或者二次开发，也可以修改其中的代码。

但请保留原文件中的版权信息，尊重本人的劳动成果，违者必究，谢谢合作。

问题与反馈

遇到问题怎么办？

• 直接提交issue

• QQ群：483350228

更新与支持

本项目(DncZeus)由码友网开源并提供更新和维护