题意：

题目给出两个矩阵X,Y,现在有两种操作
Z = X × Y
D = X⊙Y

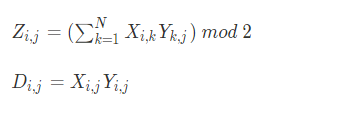
问是否存在一个矩阵C，使得A×C=B⊙C式子成立，问矩阵C能有多少个

题解：

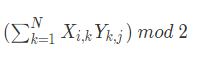
这个式子在模2意义下的加法就等于异或
也就相当于

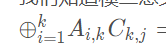
那现在有

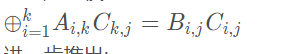
将BC移到左边

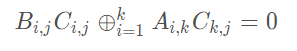
然后将Ci,j的系数进行合并得到：

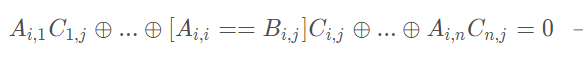
aik =Aik

A i,i = = B i,j时，A i,i xor B i,j = 0,ai,i = 0
​A i,i != B i,j时，ai,i = 1
矩阵C是列独立的，所以我们每次对Ci,j列出的向量只涉及第j列中未知数Cij
2^自由元总数即为答案个数。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N=210;
int a[N][N];//增广矩阵
int x[N];//解集
int freeX[N];//自由变元
// equ:方程个数 var:变量个数
int Gauss(int equ,int var){//返回自由变元个数/*初始化*/for(int i=0;i<=var;i++){x[i]=0;freeX[i]=0;}/*转换为阶梯阵*/int col=0;//当前处理的列int num=0;//自由变元的序号int k;//当前处理的行for(k=0;k<equ&&col<var;k++,col++){//枚举当前处理的行int maxr=k;//当前列绝对值最大的行for(int i=k+1;i<equ;i++){//寻找当前列绝对值最大的行if(a[i][col]>a[maxr][col]){maxr=i;swap(a[k],a[maxr]);//与第k行交换break;}}if(a[k][col]==0){//col列第k行以下全是0，处理当前行的下一列freeX[num++]=col;//记录自由变元k--;continue;}for(int i=k+1;i<equ;i++){if(a[i][col]!=0){for(int j=col;j<var+1;j++){//对于下面出现该列中有1的行，需要把1消掉a[i][j]^=a[k][j];}}}}/*求解*///无解：化简的增广阵中存在(0,0,...,a)这样的行，且a!=0for(int i=k;i<equ;i++)if(a[i][col]!=0)return -1;//无穷解: 在var*(var+1)的增广阵中出现(0,0,...,0)这样的行if(k<var)//返回自由变元数return var-k;//自由变元有var-k个//唯一解: 在var*(var+1)的增广阵中形成严格的上三角阵for(int i=var-1;i>=0;i--){//计算解集x[i]=a[i][var];for(int j=i+1;j<var;j++)x[i]^=(a[i][j]&&x[j]);}return 0;
}void testf(){for(int i=0;i<3;i++){for(int j=0;j<3;j++){cin>>a[i][j];}}cout<<Gauss(3,3);exit(0);
}int A[N][N];
int B[N][N];
const long long MOD=998244353;
int main(){//testf();ios::sync_with_stdio(0);int n;cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>A[i][j];}}for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>B[i][j];}}long long ans_cnt=0;for(int j=0;j<n;j++){for(int i=0;i<n;i++){for(int k=0;k<n;k++){a[i][k]=A[i][k];}a[i][n]=0;a[i][i]=(A[i][i]==B[i][j]?0:1);}int cnt=Gauss(n,n);if(cnt>0){ans_cnt+=cnt;}else if(cnt<0){cout<<0;return 0;}}long long ans=1;while(ans_cnt--){ans<<=1;ans%=MOD;}cout<<ans;return 0;
}