1. 引言

事件总线解决了微服务间如何基于集成事件进行异步通信的问题。然而只有事件总线正常运行，微服务之间基于事件的通信才得以运转。 而现实情况是，总有这样或那样的问题，导致事件总线不稳定或不可用，比如：网络中断，系统断电等等，这都可能导致微服务间的不一致性问题。 那如何解决事件总线故障导致的不一致问题呢？

1. 事件溯源

2. 事件日志挖掘

3. 发件箱模式

2. 问题

既然上面提到了一致性问题，那具体的问题是什么呢，在什么情况才会发生呢？我想我有必要简单举例。上代码：

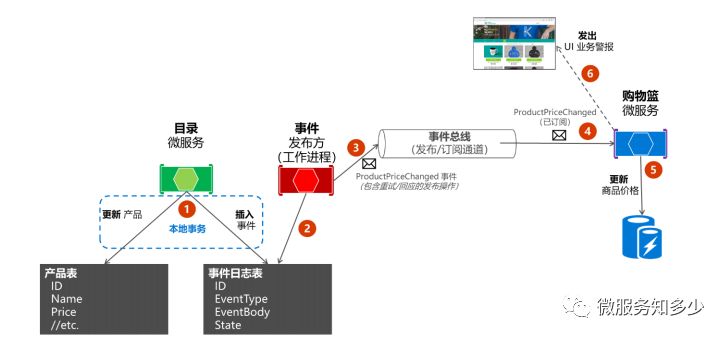
1. var oldPrice = item.Price;

2. item.Price = product.Price;

3. _context.CatalogItems.Update(item);

4. var @event = new ProductPriceChangedIntegrationEvent(item.Id, item.Price, oldPrice);

5. // Commit changes in original transaction

6. await _context.SaveChangesAsync();

7. 
   

8. // Publish integration event to the event bus

9. // (RabbitMQ or a service bus underneath)

10. _eventBus.Publish(@event);

当产品价格更改后，代码将数据提交给数据库，然后发布 ProductPriceChangedIntegrationEvent 事件。 如果服务在数据库更新后崩溃（奔溃发生在 _context.SaveChangesAsync()代码执行之后，但又发生在集成事件成功发布前），就会导致本地微服务价格已成功更新，但集成事件未发布的问题。就会导致目录微服务中定义的价格和顾客购物车中缓存的价格不一致。

3. 分析问题

以上问题的关键在于是如何确保两个独立的操作的原子性。如果单从单体应用的角度来处理的话，我们完全是可以将他们放到同一个事务中去保证。然而在微服务中，就违背了其高可用的基本要求。因为一旦事件总线处于瘫痪状态，那么整个目录微服务就不可用了。这种强制通过事务保证的一致性，就引入了太多的问题依赖。

如果从微服务的角度来看，每个微服务负责各自的业务逻辑，对于目录微服务来说，它的关注点是产品的更新是否成功。至于借助事件总线通过异步事件实现微服务间的通信，并不是其关注点。这也就是关注点分离。换句话说，产品的更新不应该依赖外部状态。在这里，外部状态就是事件总线的可用性。

你可能会说了，既然不允许通过强事务保证一致性，那么如何解决一致性问题呢（好像绕了半天又回到了原点）？

这里就要引入强一致性和最终一致性的概念了。强一致性：也就是事务一致性，将多个操作放到单一事务处理。要么全部成功，要么全部失败。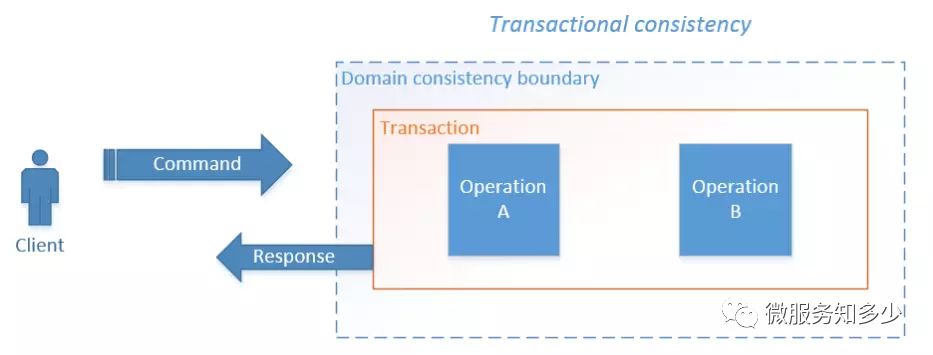最终一致性：通过将某些操作的执行延迟到稍后的时间来执行。若前面的操作执行成功，后续操作将延后执行。若前面的操作失败，后续的操作就不会执行。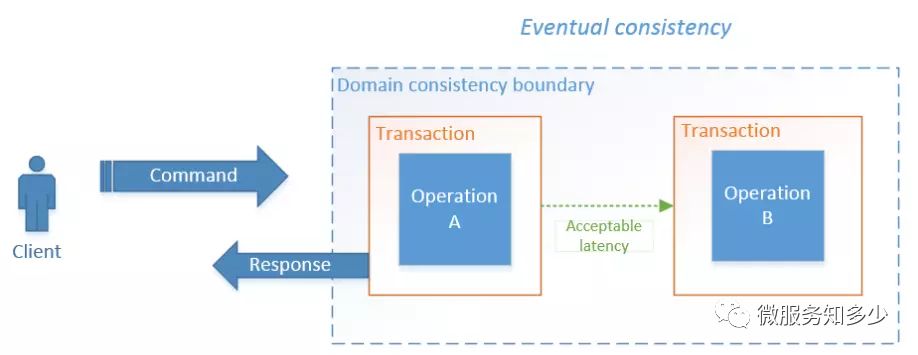

到这里，我们实际要解决的问题就明确了：如何确保事件总线能够正确进行事件转发？

换句话说：事件总线挂了，但是事件消息不能丢失。只要事件消息不丢，后面我们还有机会挽救（重新发布消息）。

如何保证事件消息不丢失呢？当然是持久化了。

4. 持久化事件源

eShopOnContainers已经考虑了这一点，集成了事件日志用于持久化。我们直接来看类图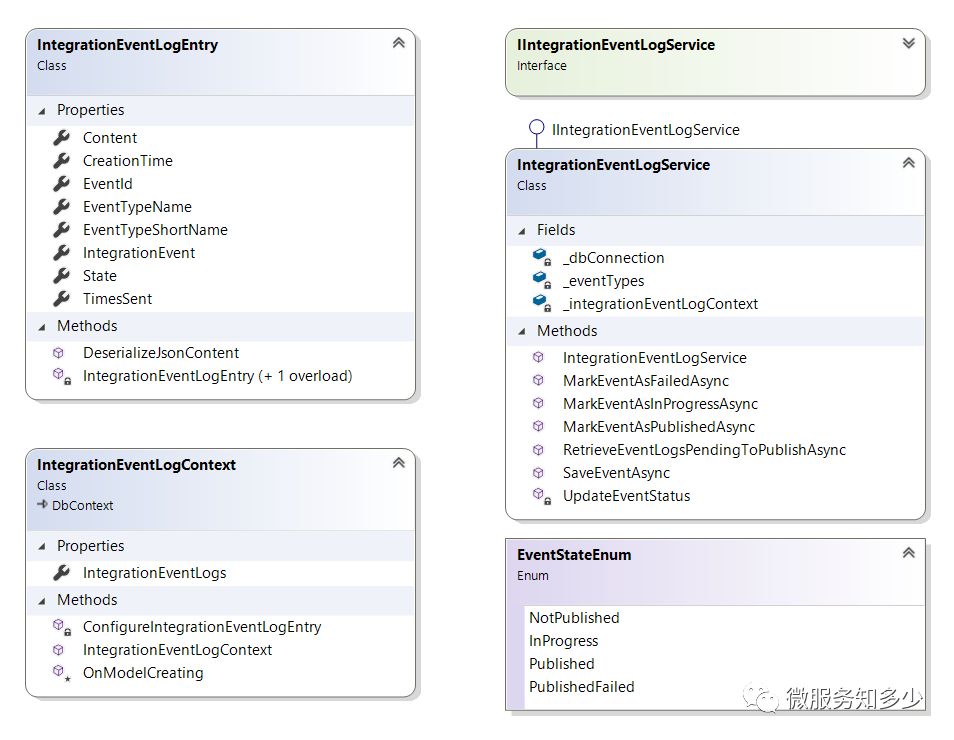：从类图中看其实现逻辑也很简单，主要是定义了一个 IntegrationEventLogEntry实体、 EventStateEnum事件状态枚举和 IntegrationEventLogContextEF上下文用于事件日志持久化。暴露 IIntegrationEventLogService用于事件状态的更新。

其他微服务通过在启动类中注册 IntegrationEventLogContext即可完成事件日志的集成。

1. services.AddDbContext<IntegrationEventLogContext>(options =>

2. {

3.    options.UseSqlServer(configuration["ConnectionString"],

4.        sqlServerOptionsAction: sqlOptions =>

5.        {

6.            sqlOptions.MigrationsAssembly(typeof(Startup)

7.                .GetTypeInfo().Assembly.GetName().Name);

8.            sqlOptions.EnableRetryOnFailure(maxRetryCount: 10,

9.                maxRetryDelay: TimeSpan.FromSeconds(30),

10.                errorNumbersToAdd: null);

11.        });

12. });

使用EF进行数据库迁移后，就会生成 IntergrationEventLog表。如下图所示：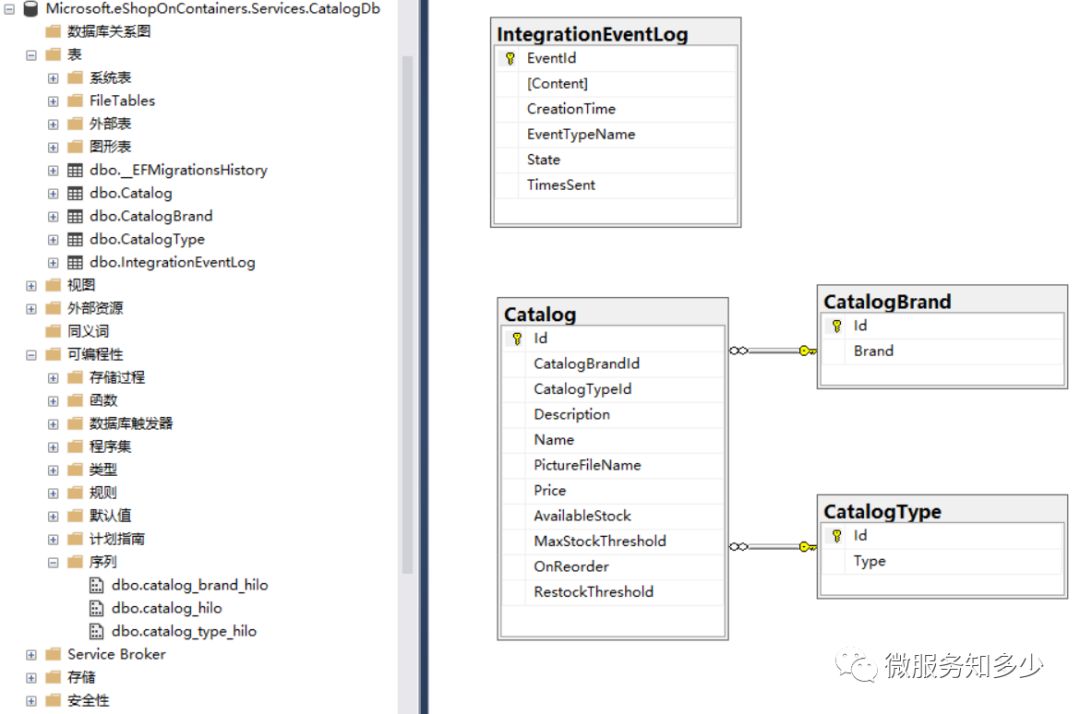

5. 如何借助事件日志确保高可用

主要分两步走：

1. 应用程序开始本地数据库事务，然后更新领域实体状态，并将集成事件插入集成事件日志表中，最后提交事务来确保领域实体更新和保存事件日志所需的原子性。

2. 发布事件

第一步毋庸置疑，第二步发布事件，我们又有多种实现方式：

1. 在提交事务后立即发布集成事件，并将其标记为已发布。当微服务发生故障时，可以通过遍历存储的集成事件（未发布）执行补救措施。

2. 将事件日志表用作一种队列。使用单独的线程或进程查询事件日志表，将事件发布到事件总 线，然后将事件标记为已发布。

这里很显然第二种方式更为稳妥。而eShopOnContainers出于简单考虑，采用了第一种方案，具体代码如下：

1. using (var transaction = _catalogContext.Database.BeginTransaction())

2. {

3. _catalogContext.CatalogItems.Update(catalogItem);

4. await _catalogContext.SaveChangesAsync();

5. // Save to EventLog only if product price changed

6. if(raiseProductPriceChangedEvent)

7. await

8. _integrationEventLogService.SaveEventAsync(priceChangedEvent);

9. transaction.Commit();

10. }

11. // Publish the intergation event through the event bus

12. _eventBus.Publish(priceChangedEvent);

13. integrationEventLogService.MarkEventAsPublishedAsync( priceChangedEvent);

至此，eShopOnContainers确保事件总线能够正确转发消息的解决方案阐述完毕。你可能会问，这对应的是引言中的哪一种方案？都不是，你可以看作其是基于事件日志的简化版的事件溯源。

6. 仅此而已？

通过持久化事件日志来避免事件发布失败导致的一致性问题，是一种有效措施。然而消息从发送到接收再到正常消费的过程中，每一个环节都可能故障，所以仅仅在消息发送端使用事件日志只是确保最终一致性的一小步。还有很多问题有待完善：

1. 消息发送成功了，但未被成功接收

2. 消息发送且成功接收，但未被正确消费

3. 消息重复发送，导致多次消费问题

4. 消息被多个微服务订阅，如何确保每个微服务都成功接收并消费

5. 等等

而这些问题就留给大家思考吧。