命令行窗口
clc 清屏
clear 清理变量

常用矩阵：

x=[0:2]'
这是转置符号x=linspace(0,2,5)
从0到2分配5个空间x=zeros(2,3)两行三列全为0的矩阵、
ones(2)2行2列全为1的方阵
eye(2)单位阵
rand(1,2)产生一行二列的随机数（从0到1之间均匀随机数）

固定变量

pi //就是π
1.00i//表示复数
inf//表示无穷大
NaN//不知道是什么数

矩阵运算和数组运算

F=A*B//这是矩阵相乘
F=A.*B//这是矩阵的点运算，对应位置相乘（注意有个点）
G=A/B //A乘以（B的逆）
H=A./B // 点除，对应位置相除
I = A^2 // 前提A是方阵，矩阵A的平方A=[ 1 2 3;4 5 6;7 8 9 ]
x=A(1,3) // 取A的第一行第三列
y=A(2,:) //取第二行所有
A(A(:,1)==2,:)=0//把第一列为0所在的行全部赋为0

数组操作

A =1     2     34     5     67     8     9
flipud(A)//旋转A7     8     94     5     61     2     3
rot90(A)//旋转90度
ans =3     6     92     5     81     4     7
sum(A)
每一列和
sum(A,2)
每一行和

A=[1 2 3];
max(A,2)//A中元素和2取max
B=[1 3 9;4 8 6];
max(B)每一列取最大值
max(B,[],2)每一行取最大值

x=0:pi/6:pi
x从0到π每次隔π/6
round()四舍五入
fix()向0方向靠
mod(x,y) x%y

基本语句

for ...end
if..else ...end
while ... end
switch...case...end求1-10以内的奇数和
x=0;
for i =1:10if mod(i,2)==1x=x+i;end
end

简单作图

x=-2*pi:0.1:2*pi;
y1 = sin(x);
plot(x,y1)

hold on//保存之前的图，不让图被覆盖

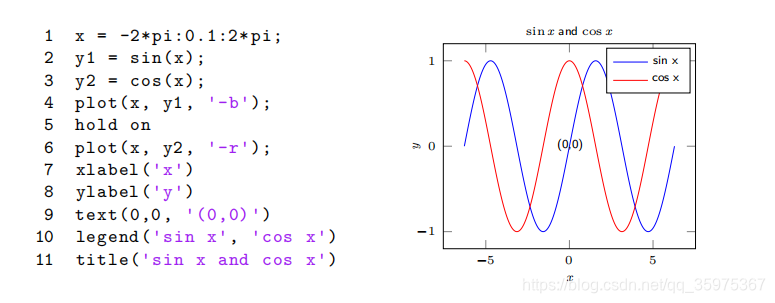
x=-2*pi:0.1:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1,'-b','linewidth',3)
hold on
plot(x,y1,'-r','linewidth',3)
xlabel('x')
ylabel('y')
text(0,0,'这是原点')在坐标(x,y)的地方标上'这是原点'
legend('sin x','cos x')右上角有个图例
title('sin x and cos x')在图顶端加个title
grid on 加网格

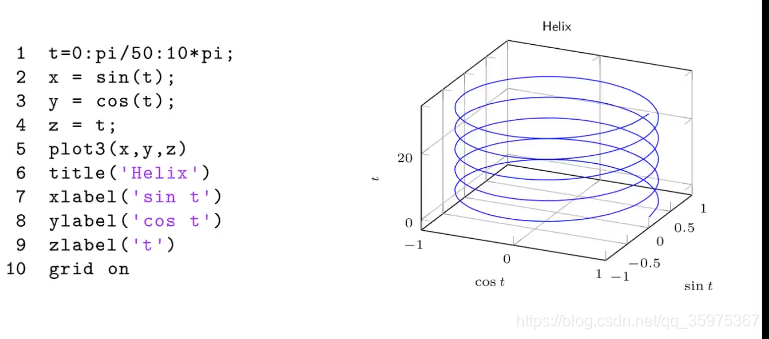
plot3(x,y,z)

meshgrid

meshgrid：网格

1、主要使用的函数为[X,Y]=meshgrid(xgv,ygv);

meshgrid函数生成的X，Y是大小相等的矩阵，xgv，ygv是两个网格矢量，xgv，ygv都是行向量。

X：通过将xgv复制length(ygv)行（严格意义上是length(ygv)-1行）得到

Y：首先对ygv进行转置得到ygv’，将ygv’复制（length(xgv)-1）次得到。

M函数

封装函数

function [area,circ] = rectarea(L,W)
% RECTARE area of a rectanglearea = L .*W;
circ = 2 * (L + W);