很难想 but很好实现
博弈论专练
传送门
惯例这里只完成D，E，F
话不多说上代码

D:Tokitsukaze, CSL and Stone Game

题目大意

输入n，n堆石子，接下来输入n个数表示i堆石子a[i]个
然后sjf先手，每人任选一堆石子，拿走一个，如果拿走后出现有至少两堆石子个数相同就输了
csl赢输出cslnb，否则输出sjfnb，每个人都选择最优选法，因为他们很聪明

n (1≤n≤10^5) a1,a2,…,an (0≤a1,a2,…,an≤10^9)

题解

每人只能取一颗，那么去到最后决胜就是n堆石子个数分别是0,1,2…n-1这样下一个人怎么选都是必输
好了这题结束，下一题 如果这么快就AC是不是太水了？那就在特判那里挖坑吧！
本仙女是被这道题的特判给弄哭了（哼唧唧╭(╯^╰)╮）

先手必输的特判：
1）如果刚开始石子就有>=2对相同的石子，那么你选了破坏了一对，另外也有一对。
2）如果有一对相同的石子，但是石子数-1也有一堆，也会输eg：5 5 4你选了5就出现了5 4 4还是有相同石子数
3）如果有一对是0，那么也是输，因为你取不了0

代码实现

#include <cstdio>
#include <algorithm>
using namespace std;
#define MAXN 100005
int tot, n;
long long sum;
int a[MAXN];
int main() {scanf ( "%d", &n );for ( int i = 1;i <= n;i ++ ) {scanf ( "%d", &a[i] );sum += a[i];}sort ( a + 1, a + n + 1 );int len = 1;if ( n == 1 && a[1] == 0 ) return ! printf ( "cslnb" );a[n + 1] = a[0] = -1;for ( int i = 2;i <= n + 1;i ++ ) {if ( a[i] == a[i - 1] ) {len ++;if ( len > 2 ) return ! printf ( "cslnb" );}else {if ( len == 2 ) tot ++;if ( tot > 1 ) return ! printf ( "cslnb" );if ( len == 2 && a[i - 1] == 0 ) return ! printf ( "cslnb" ); if ( len == 2 && a[i - 3] == a[i - 1] - 1 ) return ! printf ( "cslnb" );len = 1;}}long long tmp = n * ( n - 1 ) / 2;if ( ( sum - tmp ) % 2 ) printf ( "sjfnb" );else printf ( "cslnb" );return 0;
}

E：Tokitsukaze and Duel

题目大意

输入n,k (1≤k≤n≤10^5)，表示01字符串的长度为n，先手和后手必须选择连续的长度为k的区间把这些区间里面的01全部变为0或者1，如果这个区间本身全部都是1那么也可以进行全部变1的操作，就类似于不变嘛~！
最后谁先把这个字符串全部变为0或者1就胜利
如果先手赢输出tokitsukaze，后手赢输出quailty，都不满足输出over again
同样这两个人都聪明绝顶！会选择最优方法

题解

既然他们都很聪明，那么这道题就是问先手或者后手能否一招致胜

因为如果先手不能一招制胜，机会就给了后手，所以他就会一直破坏后手的方法，
比如后手把i区间变为1，先手就可以变为0，这样就能over again,
如果机会给了后手，后手也不能一招制胜，
机会就回到了先手，似乎先手就要赢了，no~~。

你当后手的头白秃了后手发现自己赢不了那么就恶心先手，
奶妈蔡文姬毒奶一口，不让先手赢，结果还是over again
所以如果你没有思路，输出over again应该能的一大部分分，
不过老师一般都会绑点ex

那么问题就变为了先手和后手分别一招制胜的情况，都没有就是over again

先手一招制胜的情况就是：
for循环暴力找一次看有没有一个连续k区间全部变为1或者0后能获胜

后手一招制胜的情况就是不管先手怎么搞，他都能找到一个连续k区间获胜。

那么就意味着n/2<=k后手赢必须满足这个条件，
因为如果n/2>k那么先手选择1–k后手根本不可能一次就把k+1到n全部一次操作，
那么你又会说如果后面有一部分已经连续了，后手可以赢呢！
那么这个假设就被推翻了，
仙女已经讲过了先手一招杀不死，就会恶心死后手，那么他就不会选1–k区间。

而且，满足了上面的条件后，还要for循环判断，
是不是不管先手怎么改变区间，他都能一招制胜。

代码实现

真的这两个for循环，你看我的说的很轻松简单的亚子，实际上可ex了！
要判断如果变为1和如果变为0两种情况

#include <cstdio>
#include <cstring>
#define MAXN 100005
int n, k;
char s[MAXN];
int pre[MAXN];
int main() {scanf ( "%d %d", &n, &k );scanf ( "%s", s );int len = strlen ( s );for ( int i = 0;i < len;i ++ )pre[i + 1] = s[i] - '0' + pre[i];for ( int i = 1;i <= n - k;i ++ ) {int tmp = pre[n] - pre[i + k - 1];if ( i == 1 && ( tmp == 0 || tmp == n - i - k + 1 ) ) return ! printf ( "tokitsukaze" );if ( tmp == 0 && pre[i - 1] == 0 ) return ! printf ( "tokitsukaze" );if ( tmp == n - i - k + 1 && pre[i - 1] == i - 1 ) return ! printf ( "tokitsukaze" ); }if ( n / 2 > k ) return ! printf ( "once again" );for ( int i = 2;i <= n - k;i ++ ) {if ( pre[i - 1] == 0 && pre[n] - pre[i + k - 1] == n - i - k + 1 ) continue;if ( pre[i - 1] == i - 1 && pre[n] - pre[i + k - 1] == 0 ) continue;return ! printf ( "once again" );}printf ( "quailty" );return 0;
}

E:Tokitsukaze and Strange Rectangle

题目大意

n个点n (1≤n≤2×10^5)，接下来n行每行表示i点的横纵坐标xi , yi (1≤xi,yi≤10^9)

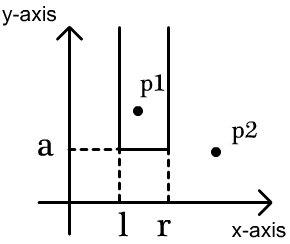
矩阵左边界l，右边界r，最下边a，无限长，问有多少个矩阵包含点的种类不一样
即yi>a,xi>l,xi<r 严格大于！的点的种类不一样，每一个i都是不一样的种类，所以如果两个矩阵分别包含1，2和2，3是属于不同的两个矩阵

题解

首先看n的范围，xi,yi的范围，数组开不了1e9就必须要离散化，
这是一个难点，做好笔记考试要考

离散化后你想，矩阵是无限高的也就意味着如果包含了i点，
也就包含了x满足这个矩阵的y>yi的所有点，那么我们就可以dfs从上往下找

接着我们思考当操作到纵坐标y的时候，
这一条直线上有多少个x点，会对答案有多少贡献：
考虑只有1个点的时候，那么就是左边有多少空与右边有多少空的乘积，

而有多个点的时候，i点左边有多少空与i点右边有多少空的乘积，
这时会重复算i点前面点已经算过的方案，所以要减掉，
其实也就是i点与i-1点之间有多少空与i后面空的乘积，
偷偷告诉你：其实单点也满足这个规律

看完后你可能会有点懵，解释一下空指的是从上往下递归后，我们会在y上所有点的x画下来，如图!
接下来的难点就是我怎么标记这个x竖线，
我们可爱的树状数组和线段树这对好基友手牵着手登上了非诚勿扰，恭喜两位嘉宾牵手成功 可以实现话不多说，屁不多放，上马！

代码实现

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define MAXN 200005
#define LL long long
struct node {LL tx, ty;LL x, y;
}a[MAXN];
vector < LL > G[MAXN];
LL n, cnt, result;
LL tree[MAXN << 2];
bool cmpx ( node u, node v ) {return u.tx < v.tx;
}
bool cmpy ( node u, node v ) {return u.ty < v.ty;
}
void update ( LL l, LL r, LL L, LL R, LL num ) {if ( l == r ) {tree[num] = 1;return;}LL mid = ( l + r ) >> 1;if ( L <= mid ) update ( l, mid, L, R, num << 1 );if ( mid < R ) update ( mid + 1, r, L, R, num << 1 | 1 );tree[num] = tree[num << 1] + tree[num << 1 | 1];
}
LL research ( LL l, LL r, LL L, LL R, LL num ) {if ( l == r ) return tree[num];if ( L <= l && r <= R ) return tree[num];LL mid = ( l + r ) >> 1;LL sum1 = 0, sum2 = 0;if ( L <= mid ) sum1 = research ( l, mid, L, R, num << 1 );if ( mid < R ) sum2 = research ( mid + 1, r, L, R, num << 1 | 1 );return sum1 + sum2;
}
void dfs ( LL u ) {if ( u == 0 ) return;LL last = 0;for ( LL i = 0;i < G[u].size();i ++ ) {LL v = G[u][i];update ( 1, n, v, v, 1 );}for ( LL i = 0;i < G[u].size();i ++ ) {LL v = G[u][i];LL t1 = research ( 1, n, 1, v, 1 );LL t2 = research ( 1, n, v, n, 1 );result += ( t1 - last ) * t2;last = t1;}dfs ( u - 1 );
}
int main() {scanf ( "%lld", &n );for ( LL i = 1;i <= n;i ++ )scanf ( "%lld %lld", &a[i].tx, &a[i].ty );cnt = 0;sort ( a + 1, a + n + 1, cmpx );for ( LL i = 1;i <= n;i ++ ) {if ( a[i].tx != a[i - 1].tx )++ cnt;a[i].x = cnt;}cnt = 0;sort ( a + 1, a + n + 1, cmpy );for ( LL i = 1;i <= n;i ++ ) {if ( a[i].ty != a[i - 1].ty )++ cnt;a[i].y = cnt;G[a[i].y].push_back( a[i].x );}for ( int i = 1;i <= cnt;i ++ )sort ( G[i].begin(), G[i].end() );dfs ( a[n].y );printf ( "%lld", result );return 0;
}

平A三刀，三杀，恭喜你成为全场MVP！！！

好了，有任何不懂的，欢迎留言，我看见了会及时给你答复