题目描述

数据范围有误！应该是不超过1e6

解析

容易推出：

y=（x$\ast$n!)/(x-n!)

换元，令t=x-n！
则：

y=n!+(n!)²/t

因为x、y都与t一一对应
所以本题就是求 (n!)² 的因数个数
我们求出n！的质因数分解的话，问题就好办了
问题在于怎么求
我们可以在预处理出[1,n]的素数表后，使用类似筛法的操作

for (int i = 1; i <= tot; i++) {for (ll j = prime[i]; j <= n; j *= prime[i]) {c[i] += n / j;c[i] %= mod;}}

为什么可以这样
我们举个例子
当n=27,模数为3时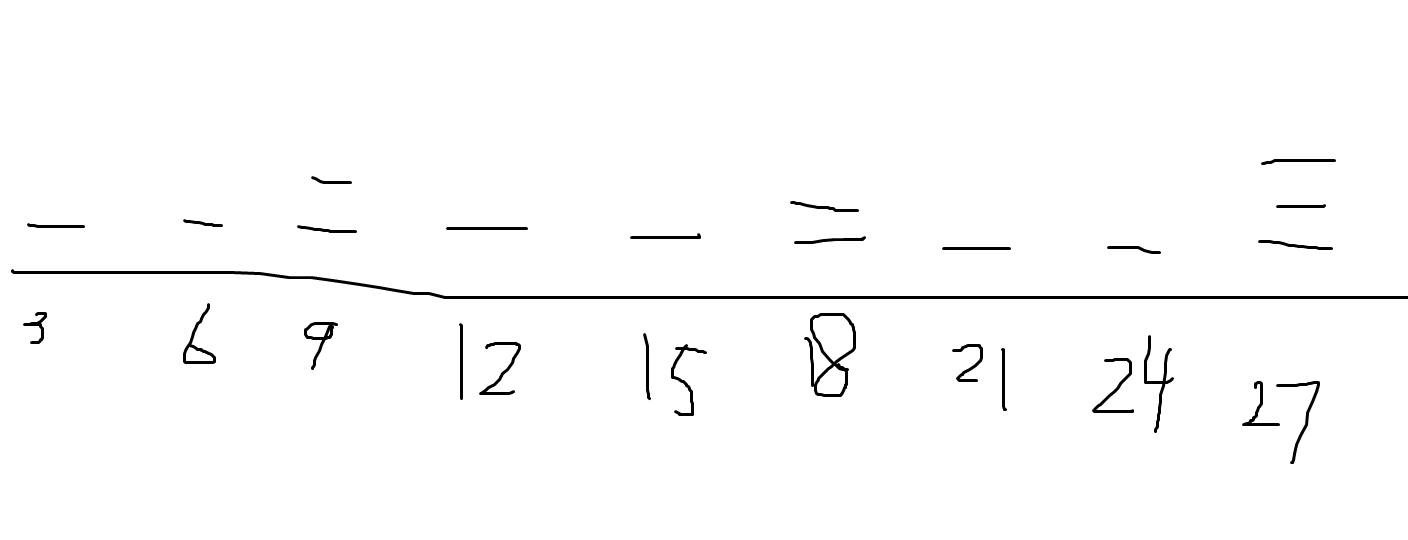
我们就是要求横线出现的次数
回去看代码
j的每一层循环其实就是在算某一层的线段个数
最后加在一起
还是挺巧妙的

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e7+100;
const int M=1e7+100;
const int mod=1e9+7;
ll n;
int prime[N],v[N],tot,c[N];
void findprime(){for(int i=2;i<=n;i++){if(!v[i]){v[i]=i;prime[++tot]=i;}for(int j=1;j<=tot;j++){int now=prime[j];if(now>n/i||now>v[i]) break;v[now*i]=now;}}return;
}int main() {scanf("%lld",&n);findprime();for(int i=1;i<=tot;i++){for(ll j=prime[i];j<=n;j*=prime[i]){c[i]+=n/j;c[i]%=mod;}}ll ans=1;for(int i=1;i<=tot;i++){ans=(ans*(2*c[i]+1))%mod;}printf("%lld\n",ans);return 0;
}