Prosjecni
【题目摘要】
描述
Slavko很无聊,所以他把正整数填到N*N的方阵中。
如果他填出来的方阵满足以下条件,他会特别高兴:
●每行中的数字的平均值是一个位于同一行的整数。
●每列中的数字的平均值是一个位于同一列的整数。
●表中的所有数字都不同。
帮助Slavko找到一种会让他开心的填法。
输入
第一行输入包含整数N(1≤N≤100)。表示方阵的行数和列数。
输出
输出N行,每行输出N个由空格分隔的整数。令第i行中的第j个数字对应于Slavko将在方阵的第i行第j列写下的值。
所有数字必须大于0且小于109。
如果有多个解决方案,则输出任意一个。
如果没有任何解决方案,则输出-1。
分数分布
无特殊分数分布。
样例输入1
3
样例输出1
1 2 3
4 5 6
7 8 9
样例输入2
2
样例输出2
-1
注意n=2时的特判
【思路+题解】
这种一看就知道不是平常套路的题
做事原则:多次试验寻找普遍规律暴力打出较简单的一组解
再玄学一波神推搞出规律(maybe not right)
刚开始我就发现n是奇数时直接1~n^2打成矩阵就是一组解了
但偶数的时候
在之后的评讲当中我重见天日Ac方法见下:
先分类讨论:
1)nnn为奇数:虽然已经知道了结论我们也要严谨推理 让我们花簇矩阵
申明:这是一个有规律的矩阵第iii行与第111行一样&&第jjj列和第111列一样
接下来的证明就以第111行和第111列为例 如果你不信可以从头证到尾俺比较懒
需要等差数列公式
行:S=(1+n)∗n/2S=(1+n)*n/2S=(1+n)∗n/2
平均数=S/n=(1+n)∗n/2/n=(1+n)/2=S/n=(1+n) *n/ 2 / n= (1+n) / 2=S/n=(1+n)∗n/2/n=(1+n)/2
nnn为奇数所以n+1n+1n+1一定是偶数
除以222一定为整&&1≤X≤n1\le X\le n1≤X≤n那么一定出现在这一行中
列:(行也可以这么证)
第一个加上最后一个S1:1+1+(n−1)∗nS1:1+1+(n-1)*nS1:1+1+(n−1)∗n
第二个加上倒数第二个S2:n+1+(n−2)∗n=S1S2:n+1 + (n - 2)*n = S1S2:n+1+(n−2)∗n=S1
…以此类推
nnn为奇数所以(n+1)/2(n+1)/2(n+1)/2就是正中间的数x,xx,xx,x的前一个等于x−nx-nx−n
xxx的后一个等于x+nx+nx+n两个相加除以二就刚好等于xxx
结合上面所有的S1,S2,S3S1,S2, S3S1,S2,S3相等可知列的平均数也一定出现
2)nnn为偶数 花簇n=4n=4n=4的情况表
多画几组可以发现前n−1n-1n−1个都是连续的
容易发现6=n∗(n−1)/26=n*(n-1)/26=n∗(n−1)/2 那么这一行的和S=n∗(n−1)S=n*(n-1)S=n∗(n−1) 平均数就是S/n=n−1S/n=n-1S/n=n−1
第i行的规律均是如此 如果你不信可以从头证到尾本仙女比较懒
因为行的规律出来了那么下一行打头的这个数就可以随意选择,但为了方便,我们可以接
着上一行最后一列的数加一打头,方便且不重复,真是太有心了
BUT唯一的bug就在最后一行的选择上你如果把倒数第二行最后一列直接加111
你发现这一列就满足不了题意,这个时候技巧就在于把行的规律照搬到列上去
而就在这个时候你惊奇地发现最后一行自动满足题意了

我们以第一列和第二列为例证明(先不看最后一行):
第二列每一个数都比第一列的数大111
按照上面行推出来的结论
自然而然第二列最后一行的数会比第一列最后一行的数大111
如此最后一行自然也满足我们的行结论了
#include <cstdio>
#define MAXN 100
int n, tot;
int num[MAXN][MAXN];
int main() {scanf ( "%d", &n );if ( n == 2 ) return ! printf ( "-1" );if ( n % 2 ) {for ( int i = 1;i <= n;i ++ )for ( int j = 1;j <= n;j ++ )num[i][j] = ++ tot;}else {int sum;for ( int i = 1;i < n;i ++ ) {sum = 0;for ( int j = 1;j < n;j ++ ) {if ( j == 1 ) num[i][j] = num[i - 1][n] + 1;else num[i][j] = num[i][j - 1] + 1;sum += num[i][j];}num[i][n] = num[i][n - 1] * n - sum;}for ( int j = 1;j <= n;j ++ ) {sum = 0;for ( int i = 1;i < n;i ++ )sum += num[i][j];num[n][j] = num[n - 1][j] * n - sum;}}for ( int i = 1;i <= n;i ++ ) {for ( int j = 1;j < n;j ++ )printf ( "%d ", num[i][j] );printf ( "%d\n", num[i][n] );}return 0;
}
 又A一道,来嗨起来!!!
又A一道,来嗨起来!!!
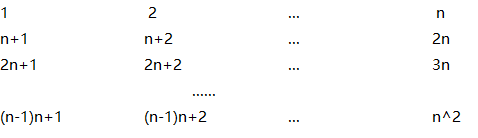


)


)

.netcore程序的服务发现)

![P6628-[省选联考 2020 B 卷] 丁香之路【欧拉回路,最小生成树】](http://pic.xiahunao.cn/P6628-[省选联考 2020 B 卷] 丁香之路【欧拉回路,最小生成树】)


)
![[HAOI2006]均分数据](http://pic.xiahunao.cn/[HAOI2006]均分数据)

)

)


