P3803 【模板】多项式乘法（FFT）

题目描述

给定一个 n 次多项式 F(x)，和一个 m 次多项式 G(x)。
请求出 F(x)和 G(x)的卷积。
从低到高输出F(x)*G(x)的系数
另一种问法：
如果有两个无限序列a和b，那么它们卷积的结果是：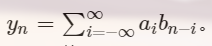
求出yn值

题解：

模板题
建议背过模板
讲的非常不错的博客

代码：

#include <cmath>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;const int maxn=2e6+5;
const double pi=3.1415926535898;
int t, n, m, len=1, l, r[maxn*2];struct Cpx{  //复数double x, y;Cpx (double t1=0, double t2=0){ x=t1, y=t2; }
}A[maxn*2], B[maxn*2], C[maxn*2];
Cpx operator +(Cpx a, Cpx b){ return Cpx(a.x+b.x, a.y+b.y); }
Cpx operator -(Cpx a, Cpx b){ return Cpx(a.x-b.x, a.y-b.y); }
Cpx operator *(Cpx a, Cpx b){ return Cpx(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x); }void fdft(Cpx *a, int n, int flag){  //快速将当前多项式从系数表达转换为点值表达for (int i=0; i<n; ++i) if (i<r[i]) swap(a[i], a[r[i]]);for (int mid=1; mid<n; mid<<=1){  //当前区间长度的一半Cpx w1(cos(pi/mid), flag*sin(pi/mid)), x, y;for (int j=0; j<n; j+=(mid<<1)){  //j:区间起始点Cpx w(1, 0);for (int k=0; k<mid; ++k, w=w*w1){  //系数转点值x=a[j+k], y=w*a[j+mid+k];a[j+k]=x+y; a[j+mid+k]=x-y;}}}
}inline int getint(int &x){char c; int flag=0;for (c=getchar(); !isdigit(c); c=getchar())if (c=='-') flag=1;for (x=c-48; c=getchar(), isdigit(c);)x=(x<<3)+(x<<1)+c-48;return flag?x:-x;
}int main(){getint(n); getint(m); int x;for (int i=0; i<=n; ++i) getint(x), A[i].x=x;for (int i=0; i<=m; ++i) getint(x), B[i].x=x;while (len<=n+m) len<<=1, ++l;  //idft需要至少l1+l2个点值for (int i=0; i<len; ++i)  //编号的字节长度为lr[i]=(r[i>>1]>>1)|((i&1)<<(l-1));fdft(A, len, 1); fdft(B, len, 1);for (int i=0; i<len; ++i) C[i]=A[i]*B[i];fdft(C, len, -1);  //idftfor (int i=0; i<=n+m; ++i) printf("%d ", int(C[i].x/len+0.5));return 0;
}