题目描述

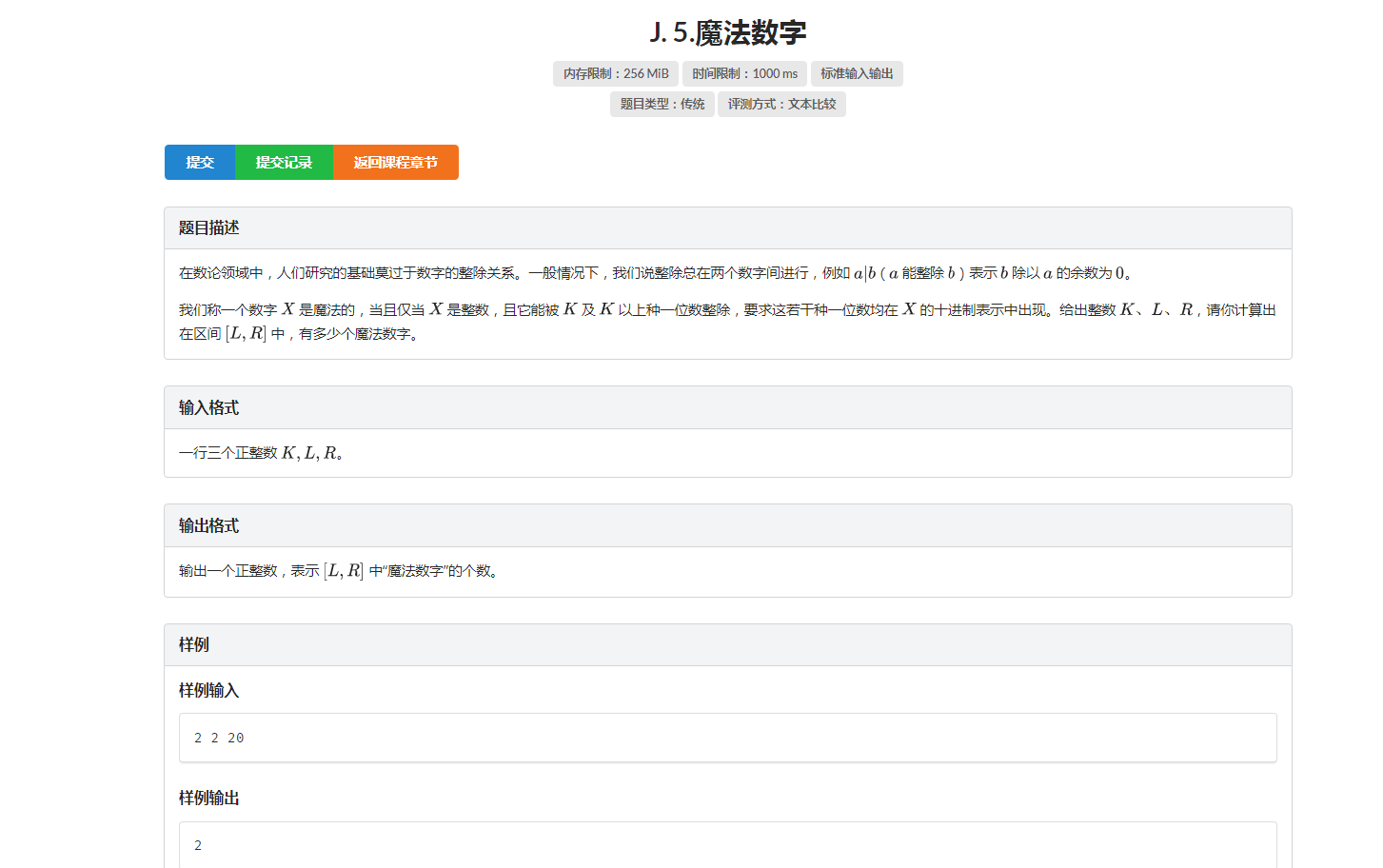
解析

迷惑。。。
首先，比较容易想到用二进制状态压缩记录1-9是否在十进制中出现过
然后就是整除的问题
如果记录余数，它的模数又有9个
开九维余数直接爆炸。。。
怎么办嘞？
有一个结论：

若ｋ为p1、p2…pn的公倍数
那么(x%k)%pi=x%pi

因为k是p的质数，所以这个结论还是挺显然的
那么本题就可以找到1-9的最小公倍数（为2520）
使它作为模数最后再进行判断即可
时间复杂度：18（位数）*512（状态压缩）*2520（取模结果）*10（每次dp枚举）=232243200
还是炸

怎么办？
位数、状压、枚举基本没有优化的空间了
但我们注意到：有些数无需记录取模结果，依靠最后一位也能判断能否整除
首先可以想到5
但其实8也可以
怎么判断？
设填到倒数第二位时，数模4的结果为m
即：

x=4k+m

再填一位i后，变成：

40k+10*m+i

显然，8能整除40k，所以只需要判断10m+i能否被8整除即可
这样公倍数那一维就不必考虑5和8，降到了252
问题得到解决

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int M = 3000500;
const int N = 200;
const int mod=252;
int k;
ll l,r,dp[20][515][255];//dp[pos][op][res]
int a[20];
int n;
ll mi[19];
ll find(int pos,int op,int res,int lim,int add5,int add8){//for(int i=pos;i<n;i++) printf("  ");//printf("pos=%d op=%d res=%d lim=%d add5=%d add8=%d\n",pos,op,res,lim,add5,add8);if(pos==0){int num=0;num+=add5&&op&(1<<(4));num+=add8&&op&(1<<(7));for(int i=1;i<=9;i++){if(i==5||i==8) continue;if(op&(1<<(i-1))&&res%i==0) num++;}//for(int i=pos;i<=n;i++) printf("  ");//printf("num=%d\n",num);ll ans=num>=k?1:0;return ans;}if(!lim&&dp[pos][op][res]!=-1) return dp[pos][op][res];ll ans=0;int mx= lim? a[pos] : 9;for(int i=0;i<=mx;i++){int oop=i?op|(1<<(i-1)):op;int aadd5=0,aadd8=0;if(pos==1){if(i==5||i==0) aadd5++;if(((res%4)*10+i)%8==0) aadd8++;}ans+=find(pos-1,oop,(ll)(i+res*10)%mod,lim&&i==mx,aadd5,aadd8);//for(int j=pos;j<n;j++) printf("  ");//printf("(i=%d ans=%d)\n",i,ans);}if(!lim) dp[pos][op][res]=ans;//for(int i=pos;i<n;i++) printf("  ");//printf("return %lld\n",ans);return ans;
}
//const int mod=1e9+7;ll solve(ll x){n=0;while(x){a[++n]=x%10;x/=10;}return find(n,0,0,1,0,0);
}
int main() {mi[0]=1;for(int i=1;i<=18;i++) mi[i]=mi[i-1]*10;memset(dp,-1,sizeof(dp));//	k=2;
//	int now=0,pre=0;
//	for(int i=1;i<=10500;i++){
//		now=solve(i);
//		if(now==pre+1) printf("%d\n",i);
//		pre=now;
//	}scanf("%d",&k);//printf("k=%d",k);scanf("%lld%lld",&l,&r);printf("%lld\n",solve(r)-solve(l-1));return 0;
}
/*
2 2 20
*/