最近公司预生产环境.net core应用的docker容器经常出现内存暴涨现象，有时会突然吃掉几个G,触发监控预警，造成容器重启。

分析了各种可能原因，修复了可能发生的内存泄露，经测试本地正常，但是发到预生产还是会有内存暴涨现象，反而更改GC模式后内存使用保持较低水平，百思不得其解，所以想到使用调试dump文件方式来分析应用内存状况。

环境：

lldb:3.9

dotnetcore:2.1.6

docker image:microsoft/dotnet:2.1.6-aspnetcore-runtime

(根据文档，dotnetcore2.0需要使用lldb3.6,但是我尝试了没有成功，lldb使用的dotnetcore版本与dump应用的dotnetcore版本要一致，由于core2.1现在官方只提供2.1.6的runtime文件，故本次测试使用2.1.6版本，如果哪位童鞋在core2.0上调试成功了，麻烦告诉我方法)

linux下需要使用lldb来进行dump分析，但是安装这个太慢，所以我找了个安装好的docker image使用，有兴趣的也可以自行安装，这里就不介绍安装过程了,.net core 本身提供了lldb sos 插件，只要加载使用就好。

启动一个.net core应用容器，这里需要多加几个参数，不然无法创建dump(另外多说一句，docker内crash coredump文件无法生成也是权限原因，我这边启动时都给了权限,如果仅仅是需要使用.netcore提供createdump工具，只需要加--privileged=true)：

docker run -d -p 80:80 --name dumptest --ulimit core=-1 --security-opt seccomp=unconfined --privileged=true dumptest:v1

--ulimit core=-1 　　　　　　　　　　   不限制coredump大小
--security-opt seccomp=unconfined 　　允许容器执行全部系统调用
--privileged=true 　　　　　　　　　　 允许createdump访问其他进程

进入容器：

docker exec -it dumptest /bin/bash

创建dump文件:

/usr/share/dotnet/shared/Microsoft.NETCore.App/2.1.6/createdump 1

(经观察，容器内的跑的应用进程ID都是1，所以直接使用，也可以使用top命令来查看进程ID,创建dump文件在/tmp/coredump.1)

退出容器：

exit

在宿主机创建文件夹/data/docker，并将容器中的dump文件拷贝到宿主机：

cd /&&mkdir data&&cd data&&mkdir docker

docker cp dumptest :/tmp/coredump.1 /data/docker

拉取lldb镜像（此镜像是lldb3.9的dotnetcore版本为2.1.5，有其他需求请自行查找）：

docker pull yyoda/dotnet-lldb

启动lldb容器,并将coredump文件路径映射到容器内(如果想要长期使用不要带--rm参数)：

docker run -d -v /data/docker:/dump --rm -it --name lldb yyoda/dotnet-lldb:latest /bin/bash

镜像内需要安装dotnetcore2.1.6,为了方便安装，在容器内部使用阿里源：

cd /data/docker
touch sources.list

将下面的源加入sources.list:

deb http://mirrors.aliyun.com/ubuntu/ trusty main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-security main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-updates main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-proposed main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-backports main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-security main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-updates main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-proposed main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-backports main restricted universe multiverse

进入lldb容器：

docker exec -it lldb /bin/bash

更新源：

mv /dump/sources.list /etc/apt/source.list
apt-get update

安装dotnetcore2.1.6 runtime(由于网络等原因，如果失败多试几次)：

wget -q https://packages.microsoft.com/config/ubuntu/14.04/packages-microsoft-prod.deb
dpkg -i packages-microsoft-prod.deb

apt-get install apt-transport-https
apt-get update
apt-get install dotnet-runtime-2.1

启动lldb:

lldb-3.9 dotnet -c /dump/coredump.1 -o "plugin load /usr/share/dotnet/shared/Microsoft.NETCore.App/2.1.6/libsosplugin.so"

（如果sos加载失败，启动后输入命令：plugin load /usr/share/dotnet/shared/Microsoft.NETCore.App/2.1.6/libsosplugin.so

   如果runtime加载失败，启动后输入命令：setclrpath /usr/share/dotnet/shared/Microsoft.NETCore.App/2.1.6）

输入soshelp命令，出现下图：

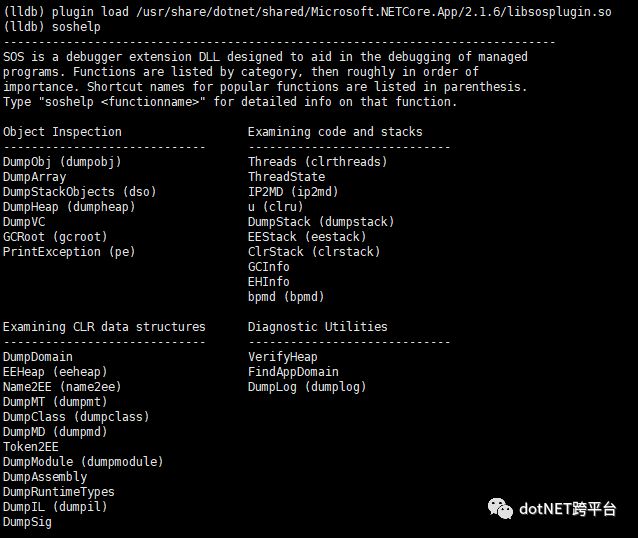
查看堆上的对象类型分配情况（由于结果太多，这里加入大于1024byte过滤）：

dumpheap -stat -min 1024

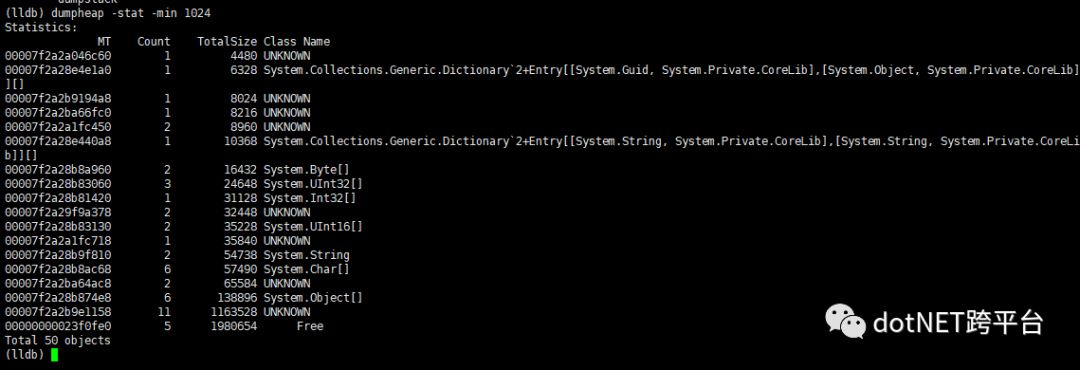
查看指定类型对象情况：

dumpheap -mt 00007f2a28b874e8 -min 1024

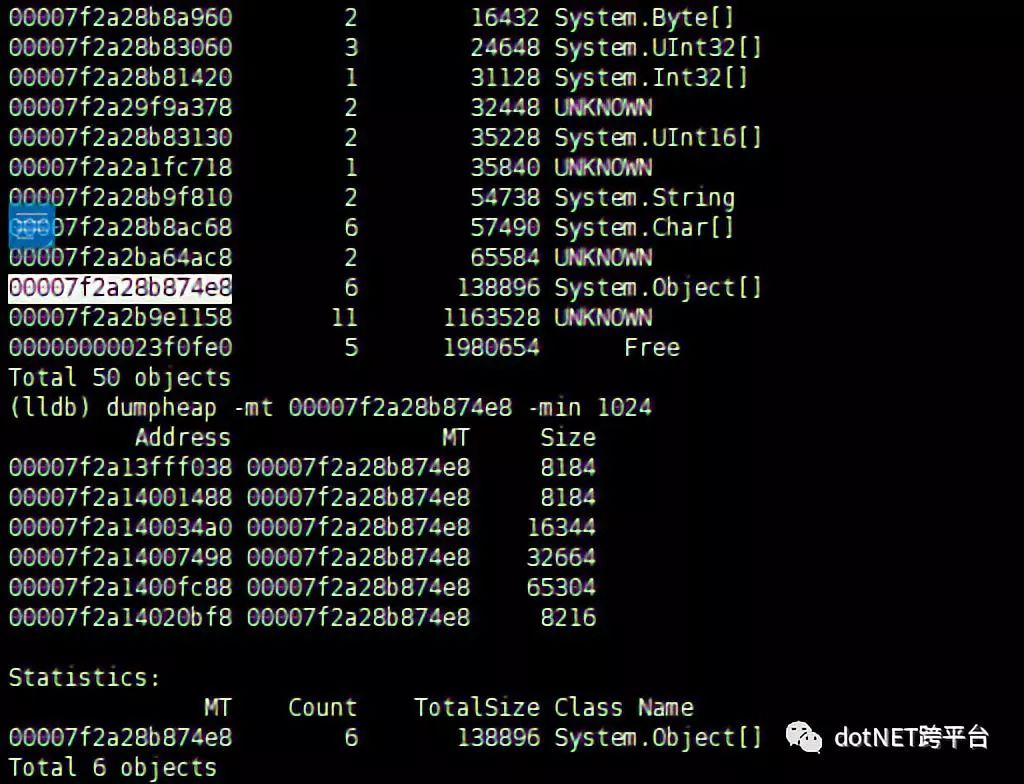
查看指定对象情况：

dumpobj 00007f2a1400fc88

剩下的就是熟悉sos命令，不在赘述了，大家自行研究吧。。。 

ps:附上docker容器内应用崩溃时生成dump方法：

1.容器启动时要带下面两个参数：

　　--ulimit core=-1 
　　--security-opt seccomp=unconfined 

2.宿主机上执行命令，更改dump文件输出路径：

　　echo '/tmp/core.%t.%e.%p' | sudo tee /proc/sys/kernel/core_pattern

　　（因为系统在产生 coredump 文件时是根据 /proc/sys/kernel/core_pattern 的设定模板来的，而默认的设定是 /usr/share/apport/apport %p %s %c %P，也就是用管道传apport。然而 Docker 里面的系统不一定有装 apport，并且 /proc 又是直接挂到 Docker 里面的，所以需要设置固定存放位置 /tmp。

　　　　%p 所dump进程的进程ID

　　　　%t core dump的时间 

　　　　%e 程序文件名）

测试：

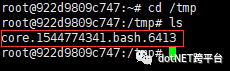
　　进入容器后执行 kill -s SIGSEGV $$   触发当前shell终端的段错误。

　　再次进入容器，在/temp路径下可以看到刚刚生成的dump文件

　　

参考资料：

https://github.com/mikem8361/coreclr/blob/5c22cb85c7cc9173f2fb783bf24c0cbbb6096c89/Documentation/building/debugging-instructions.md

http://blogs.microsoft.co.il/sasha/2017/02/26/analyzing-a-net-core-core-dump-on-linux/

原文地址：https://www.cnblogs.com/iamsach/p/10118628.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com