Quadratic Form

题意：

一个n * n 的正定矩阵和一个n维的向量b，现在找一个x1，x2，…xn满足以下条件：

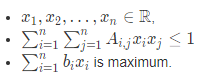
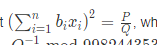
求这个式子，最后输出P * Q^-1 mod 998244353.

题解：

参考
线性代数学过n阶正定的实矩阵等价于n阶对称实矩阵
由第二个条件可得x^TAx<1.也就是A是一个正定二次型
x是一个列向量
根据KTT条件

我们定义拉格朗日函数L(x,λ)=b^T x+λ(x^TAx−1)对x求导
对二次型求导x^TAx求导，能得到2Ax

∂L(x,λ)/∂x=b+2λAx
根据不等式约束条件下的最值情况下，
b+2λAx=0，，λ>=0，λ(x^TAx−1)=0
得到 x= -A^-1b/(2λ)
然后把x带入λ(x^TAx−1)=0中
并且 A^-1= （A^-1）^T

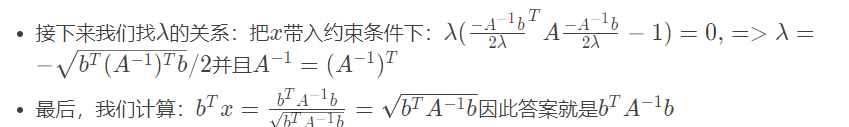
答案就是b ^T A ⁻¹ b
这种题。。。真的不会。。。

代码：