线段树合并、分裂

基本概念：

如果需要维护许多个大小为 \(10^5\) 级别的多重集，可以看做给每一个多重集建立一棵线段树。线段树的合并、分裂就是多重集的累加、分开。

这里使用动态开点的方式存储线段树树。

如果一个节点为空，那么它的编号为 \(0\) 。

变量释义：

有 \(cnt\) 个多重集
建立了 \(tot\) 个节点
若一个多重集的编号为 \(x\) ，它的根节点编号为 \(root[x]\)

注意：空间是个谜！能开多大是多大

线段树合并

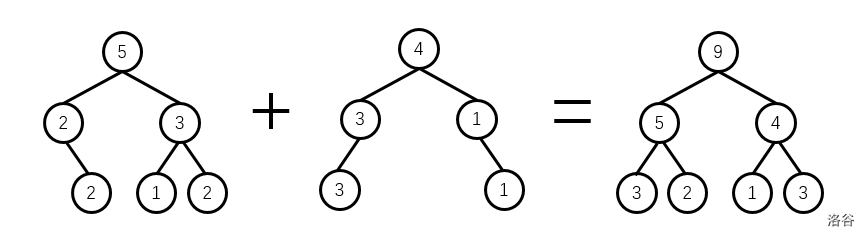
把以 \(y\) 为根的线段树合并到以 \(x\) 为根的线段树：

int merge(int x,int y,int nl,int nr) // i:y->x
{if(!x || !y) return x+y;int mid=(nl+nr)>>1;//tree[x].sum+=tree[y].sum; 根据题目改动tree[x].ls=merge(tree[x].ls,tree[y].ls,nl,mid);tree[x].rs=merge(tree[x].rs,tree[y].rs,mid+1,nr);//pushup(x);del(y);return x;
}

复杂度 \(=\) 节点数 ( 一般均摊下来可以达到一次操作 \(O(\log n)\) 的级别 )

线段树分裂

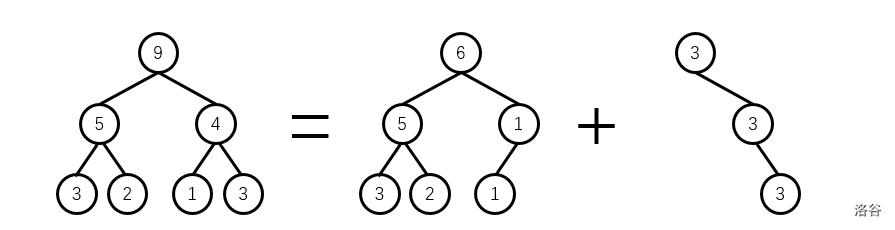
把以 \(x\) 为根的线段树中 \(\ge k\) 的数转移到一棵空的线段树 \(y\) 。

void split(int &x,int &y,int nl,int nr,int k) // i>=k i:x->y
{if(!x) x=++tot;if(!y) y=++tot;if(nl==nr) { swap(x,y); return; }int mid=(nl+nr)>>1;if(mid>=k){swap(tree[x].rs,tree[y].rs);split(tree[x].ls,tree[y].ls,nl,mid,k);}else split(tree[x].rs,tree[y].rs,mid+1,nr,k);pushup(x),pushup(y);
}