参考文献：
博文1
博文2
博文3

引入

在一类树上动态规划问题中,题目给出的询问往往包含树上的很多各节点,并保证总的点数规模小于某个值.

如果我们直接在整颗树上进行dp的话,时间复杂度与询问的次数有关,这显然是不可接受的,如果我们可以找到一种动态规划的方法,使其时间复杂度与询问中点的实际规模相关就好了.

于是虚树应运而生.

虚树

虚树并不是真实的树，是根据题意而构造的新树
虚树相比于原本，仅仅保留有用的点，重新构造一棵树
这里有用的点是指询问的点（也就是关键点）和它们的lca
（可以理解为我们只需要保存关键点即可，但为了使得关键点彼此可以构造成树，所以要保留lca）
有用的点都是位于叶子节点

具体步骤

预处理我们对整棵树进行dfs序，得到dfn[u]
我们使用一个栈，从栈顶到栈底的元素形成虚树的一颗树链。栈内元素越往上（越靠近栈顶），越靠近树链的叶子节点

对于第一个询问点，无条件加入栈stack内
然后对于所有询问点依次加入，假设当前询问点为now，lc为now和栈顶点stack[top]的最近公共祖先，lc=lca(stack[top],now)
lc和stack[top]肯定是一条链上，但是栈内其他元素与lc是什么关系呢？

情况1

lc = stack[top]
此时now在stack[top]的子树里，那我们只需要把now压入栈即可，此时now为该链的末尾，成为新的stack[now]

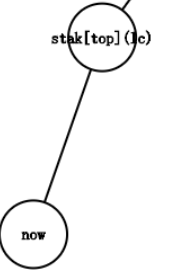
情况2

lc在stack[top]和stack[top-1]之间
那么now和stack[top]就是位于不同的子树里
如图：

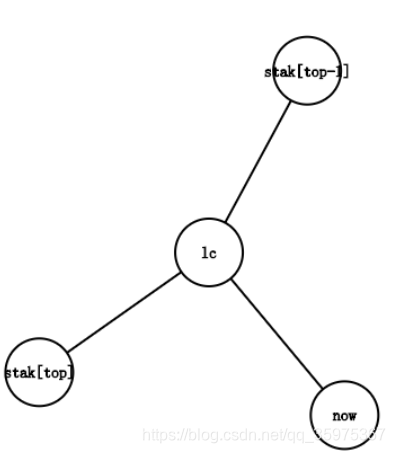
针对这种情况，树链的的末端从stack[top-1]->stack[top]变成stack[top-1]->lc->stack[top]，我们要做的就是先将边lc->stack[top]加入虚树中，然后stack[top]出栈，lc和now依次入栈。
你会发现相当于最左侧这个链已经维护完毕了，我们已经开始维护stack[top-1]->lc->now这个链

特殊变形

当lc=stack[top-1]，也就是lc和stack[top1]重合了，基本和上面是一样的，唯一的区别就是lc不用入栈（因为本来就在栈内）

情况3

dep[lc] < dep[stack[top-1]]
说明lc不在stack[top-1]的子树里，当然也可能不再stack[top-x]的子树里（x从1到…）,但会在stack[top-x-1]子树里

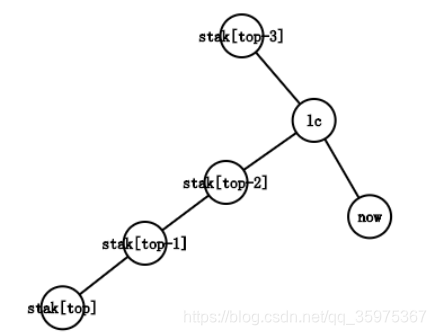
以图为例，链由stack[top-3]->stack[top-2]->stack[top-1]->stack[top]变成了stack[top-3]->lc->now，我们需要循环将右侧的末端剪下，将剪下的边加入到虚树里，直到不再是情况3，然后再按照情况二来构建（将lc和now加入其中）
当最后一个询问点加入之后，再将栈内的链加入到虚树里，完成所有构建

情况4

对于栈，我们从1开始储存，这种情况下stack[top-1]=0,dep[0]=0
此时dep[lc]<dep[stack[top-1]]恒成立
stak[0]扮演了深度最小的哨兵，确保了程序只会进入情况一和二

如何在一次询问结束后清空虚树：
在dfs过程中每当访问完一个结点就进行清空即可

例题：

P2495 [SDOI2011]消耗战