本周更新两篇，保证不太监！

在本系列教程中，笔者希望将必要的知识点围绕理论、流程（工作流程）、方法、实践来进行讲解，而不是单纯的为讲解知识点而进行讲解。也就是说，笔者希望能够让大家将理论、知识、思想和指导应用到工作的实际场景和实践之中，而不是拿着字典写文章，抱着宝典写代码。至于很多具体的语法、技术细节，除了常用的知识点，笔者更希望大家阅读官方文档——毕竟看官网比看书靠谱多了，官网会一直更新和改进，而书和教程自出版或发布之后，基本上就“死“了。

本系列教程预计全部完成还需要2到3个月的时间。在这个过程中，您可以加入我们的QQ群（85318032）一起讨论、交流和分享这一块的技术。我们也希望得到大家的支持，请多多点赞或者打赏一杯咖啡，你们的支持是我们前进的最大动力！

使用Tencent Hub来完成CI

关于Tencent Hub

Tencent Hub是腾讯出品的DevOps服务。主要提供多存储格式的版本管理，支持Docker Image、Binary、Helm Charts 等多种类型文件。同时提供 DevOps 工作流的编排引擎，并且支持编排 DevOps 工作流，以打造更强的持续集成与持续交付力，加快软件迭代发布速度。

相比Azure DevOps，Tencent Hub主要面对国内开发者，因此在CI这块，更容易水土相符。

使用Tencent Hub配置一个简单的CI流程

在开始之前，我们先得开通Tencent Hub 服务。这些前置条件我们就不再赘述了。

在本篇教程中，我们使用Tencent Hub工作流来自动拉取代码并且构建、推送镜像到容器服务镜像仓库，并且通过镜像触发器来自动触发服务更新。

主体配置流程

使用Tencent Hub的话，整个配置过程比较简单，主体配置流程如下所示：

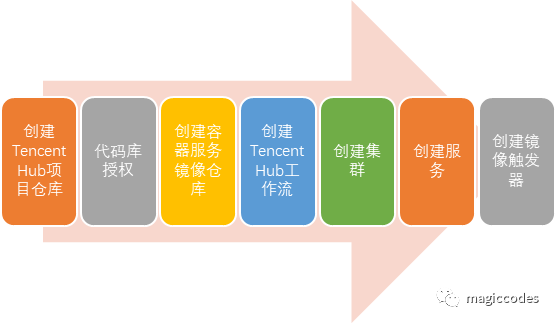
创建Tencent Hub项目仓库

在开始之前，我们需要在Tencent Hub上创建一个项目仓库，如下图所示：

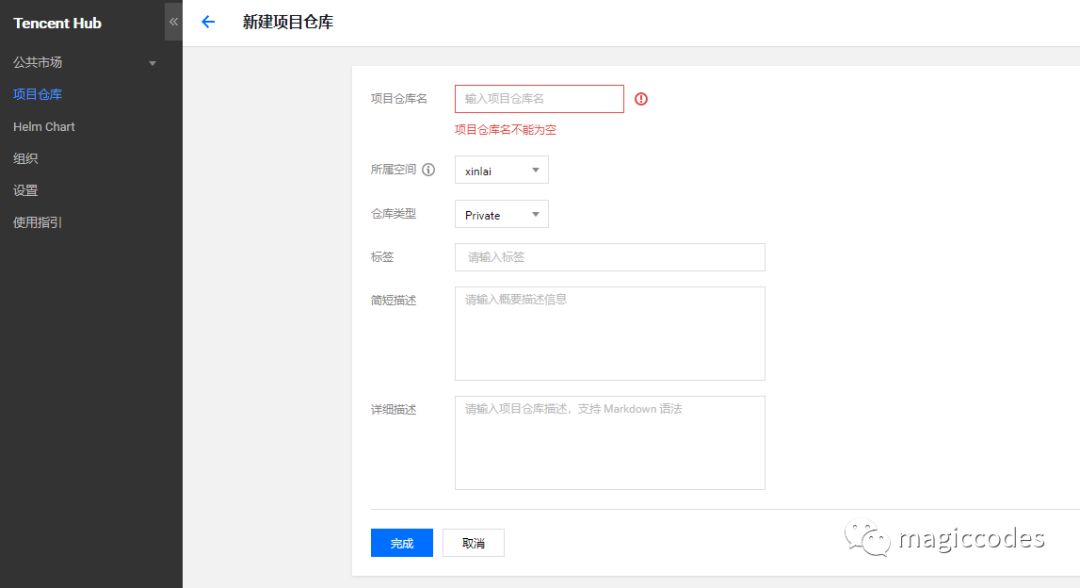
创建完成后如图所示：

至此，项目仓库创建完成。

注意：Tencent Hub项目仓库实质上是一个镜像仓库，可以存放我们构建的docker镜像。

代码库授权

仓库创建完毕，接下来我们需要进行代码库授权，以便工作流能够获取代码以及自动触发构建。首先，我们先点击设置界面，打开如下所示的界面：

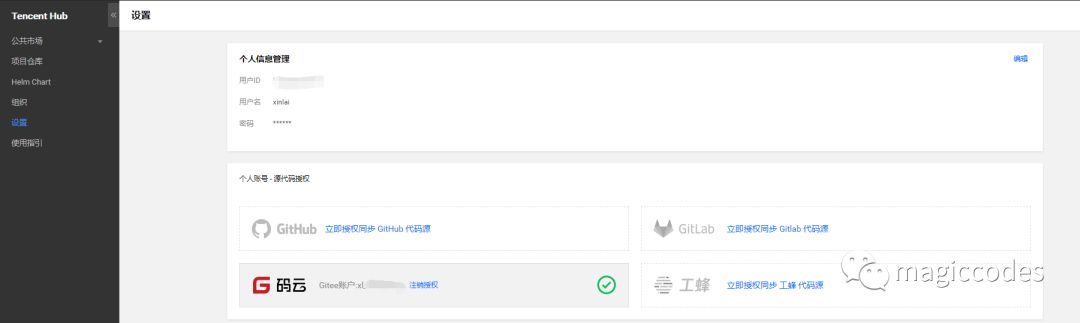
如图所示，代码库授权支持github、gitlab、码云和工蜂，这里笔者选择了码云，用于演示。

创建容器服务镜像仓库

虽然我们已经创建Tencent Hub的镜像仓库，但是为了方便，笔者建议大家还创建腾讯云容器服务的镜像仓库，以便使用默认的触发器来触发服务更新。相比使用工作流来实现，更加稳定和易于维护。腾讯云容器服务镜像仓库界面如下所示：

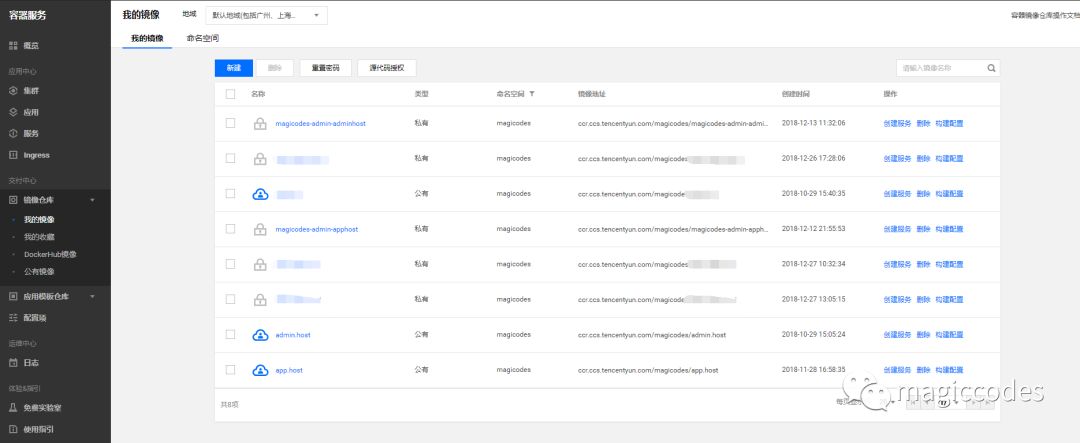
创建之后，我们就可以获得完整的镜像仓库地址，如下图所示：

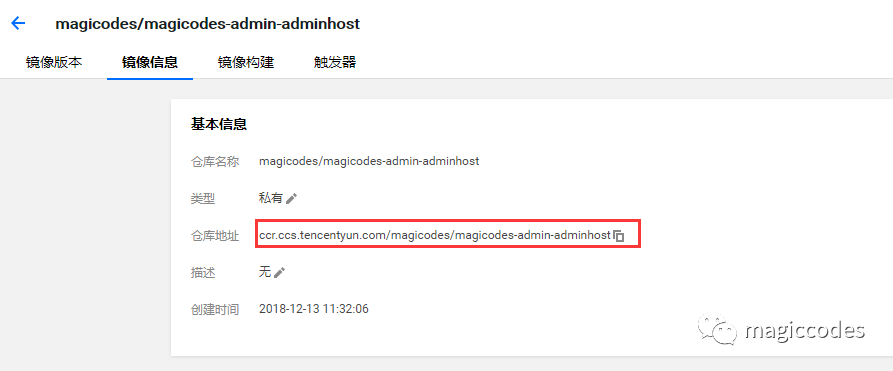
创建Tencent Hub工作流

刚才，我们已经创建了Tencent Hub项目仓库了，首先我们需要点击项目名称进入详细界面：

然后点击【工作流】选项卡打开工作流界面：

点击【新建】按钮，我们可以创建自己的工作流。

Tencent hub提供了很多工作流组件，基本上能够满足我们的需要，如下图所示：

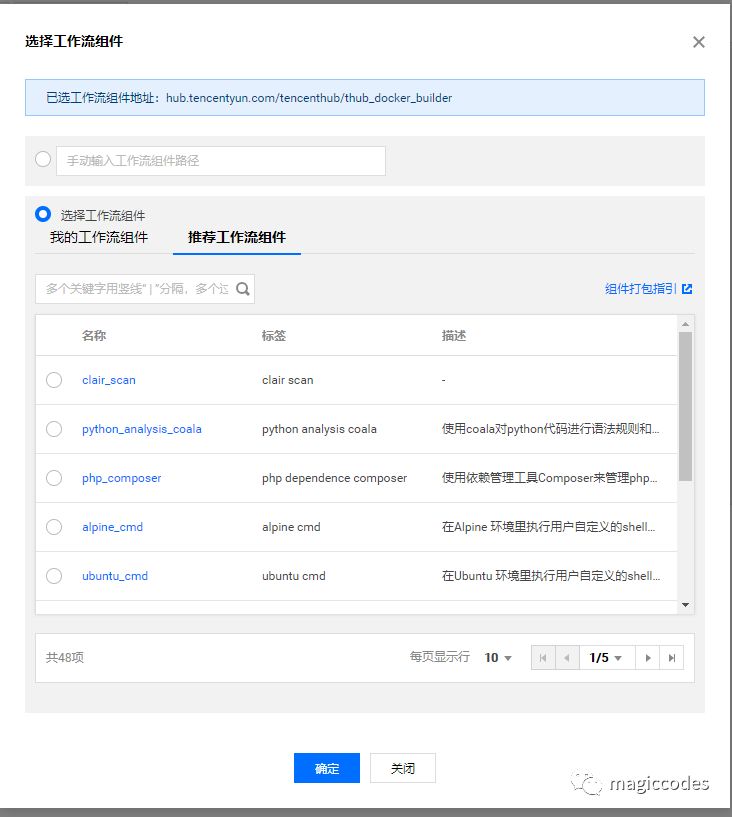
创建一个简单的工作流

接下来，我们一起来创建一个简单的工作流，主要包括以下步骤：

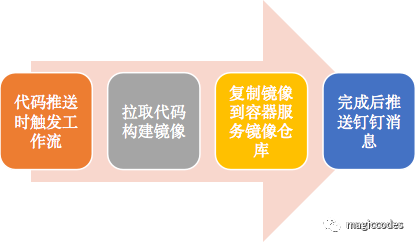
在Tencent Hub上，工作流设计界面如下所示：

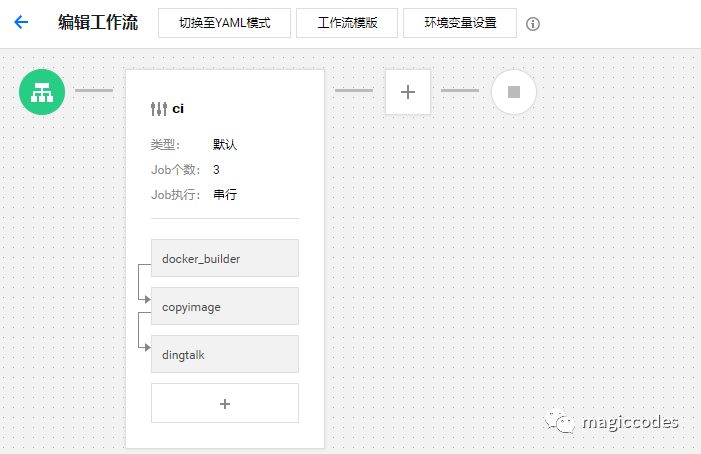
• 代码推送时触发工作流

  首先，创建工作流时，我们需要进行如下所示的设置：
  

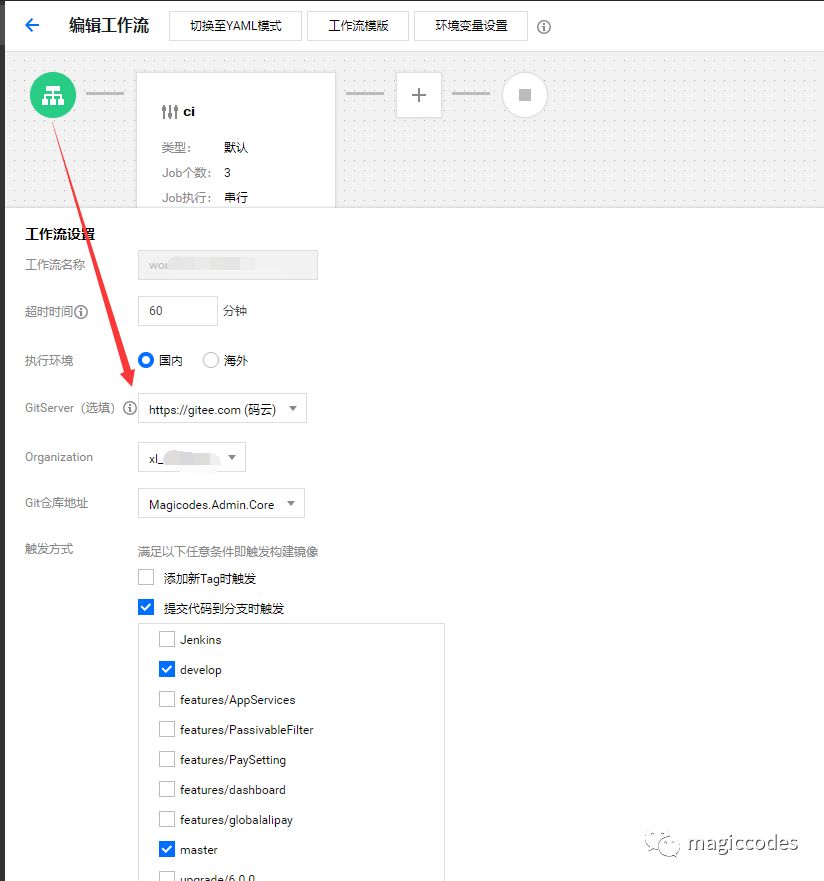
这里，我们勾选develop和master分支推送时触发工作流。

• 拉取代码构建镜像

  这里，我们需要借助工作流组件

  hub.tencentyun.com/tencenthub/thub_docker_builder来完成进行过构建。

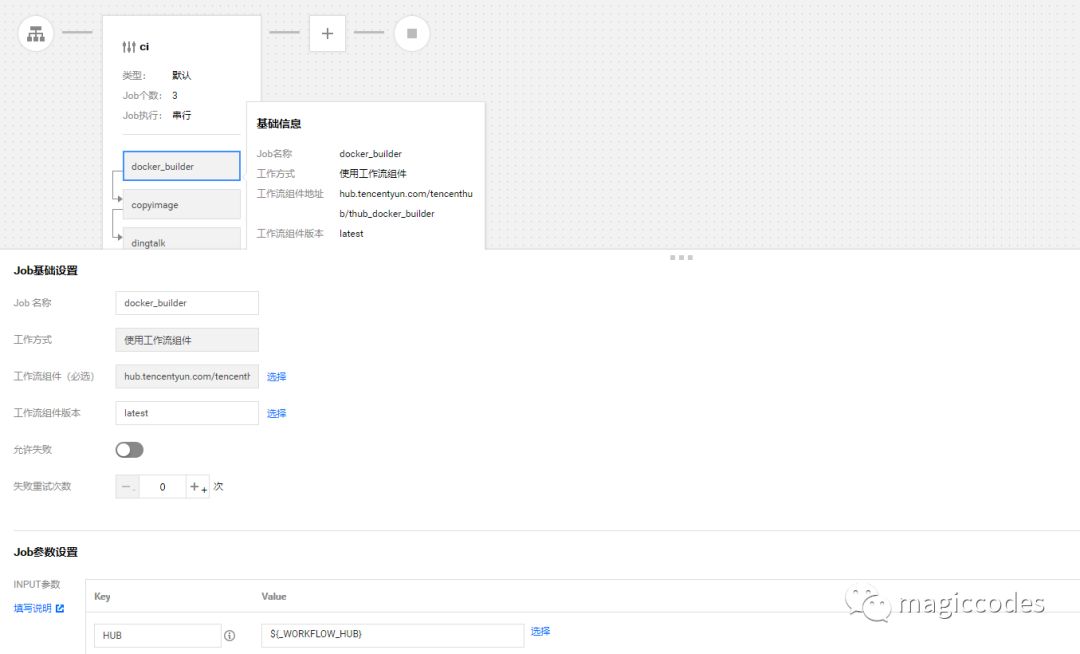
这里，我们通过YAML文件来查看具体的配置参考：

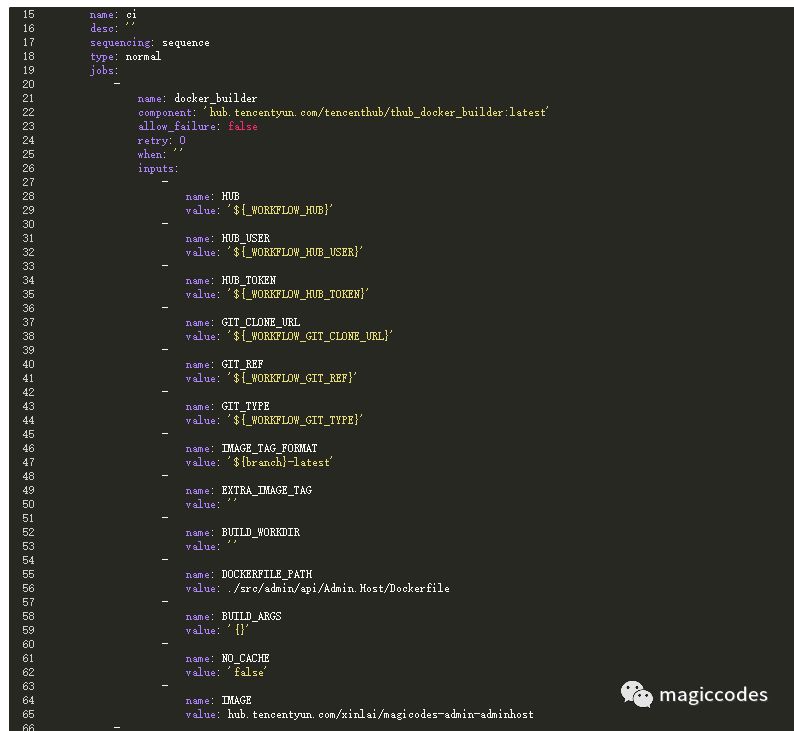
组件参数说明如下所示：

Tencent Hub的工作流组件均已开源，我们也可以直接查看源代码（有时候如果开发文档没有及时更新，照着文档配置可能会入坑），如下图所示：

注意：这里笔者追加了标签，使用到了分支名称。也就是develop分支的代码构建的镜像会打上develop-latest的标签，master类似，以便于服务部署时能够区别开来。

• 复制镜像到容器服务镜像仓库

  镜像构建成功之后，我们需要将镜像复制到容器服务镜像仓库。这里特此说明一下，之所以添加此步骤，是因为通过容器服务的镜像仓库的触发器触发服务更新更稳定以及更易于维护。事实上，大家也可以通过工作流来完成服务的更新，但是相关参数的配置颇为麻烦，而且很容易配错。

这里，我们用到的组件为：

hub.tencentyun.com/tencenthub/copy_image

组件说明如下所示：

配置参考如下所示：

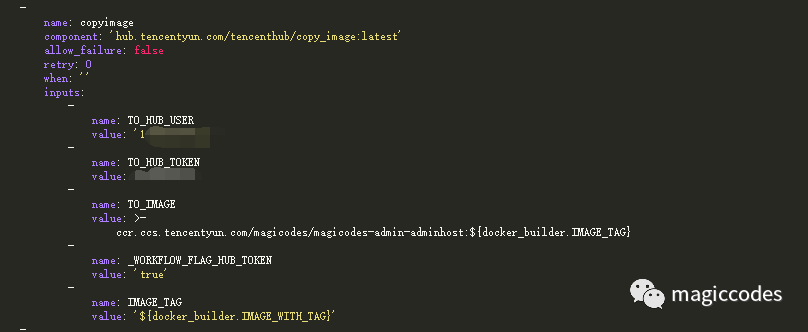
• 完成后推送钉钉消息

  镜像复制完成，我们希望能够在相关的开发组、运维组接收到消息。Tencent Hub这边也有成熟的轮子

  ——hub.tencentyun.com/tencenthub/notice_dingding。

具体如下所示：

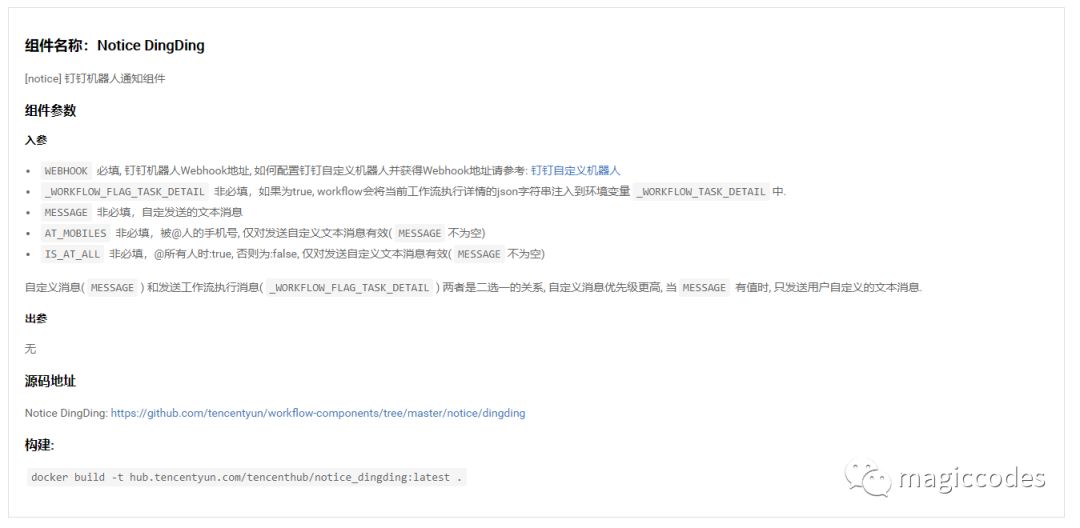
相关的配置也比较简单，不过我们需要创建一个钉钉自定义机器人：

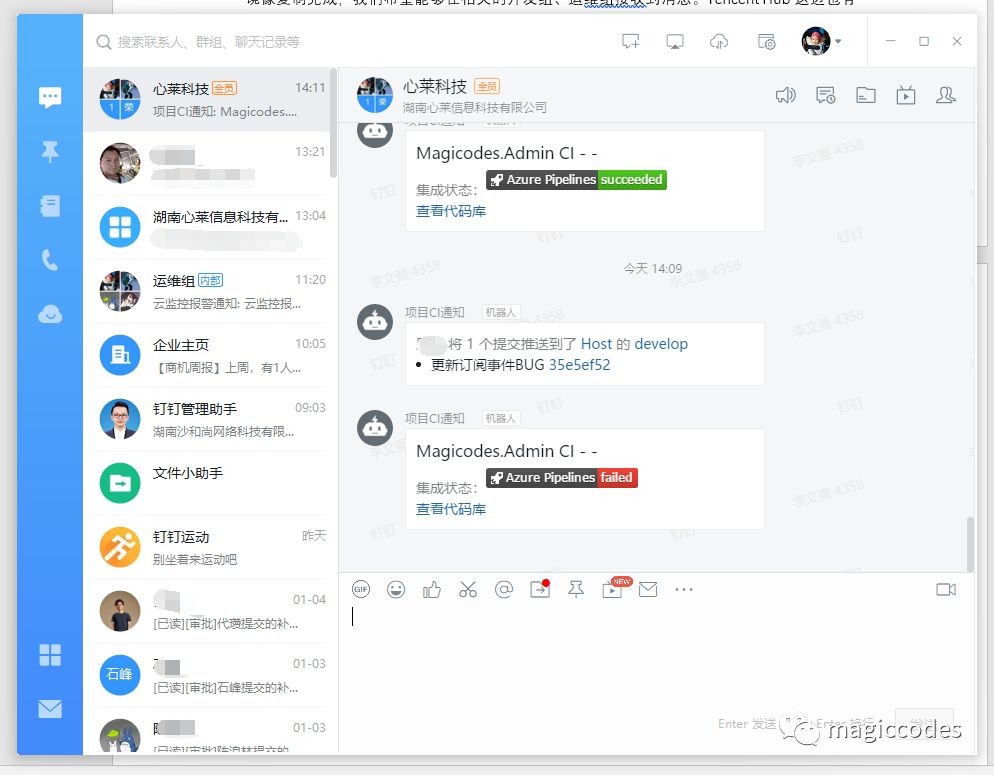
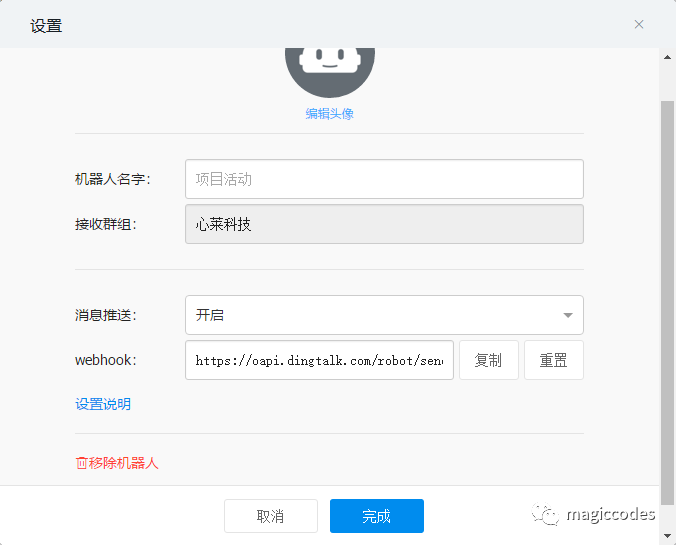
然后，我们就可以使用此工作流组件进行配置：

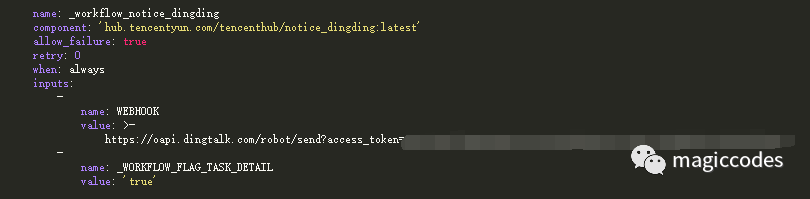
至此，整个工作流就配置完成了。当然，我们也可以在工作流的结束节点添加webhook通知，只是没法设置消息模板，如下所示：

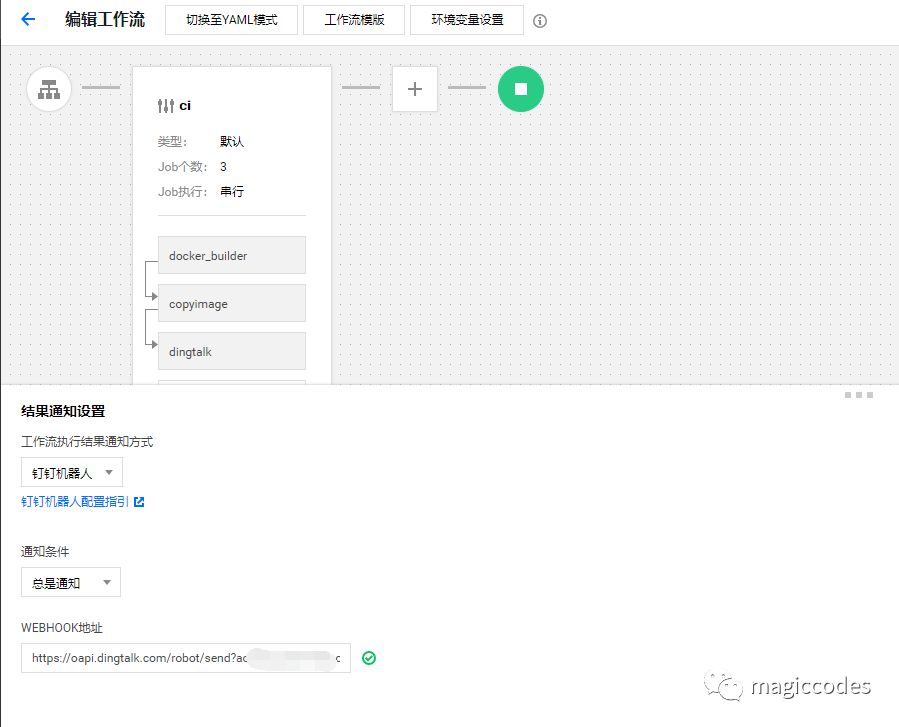
至此，整个工作流就介绍完毕。大家也可以根据自己的需要来设计符合自己要求的工作流。

当代码提交时，就会自动触发构建，我们在工作流界面可以看到当前状态以及执行历史：

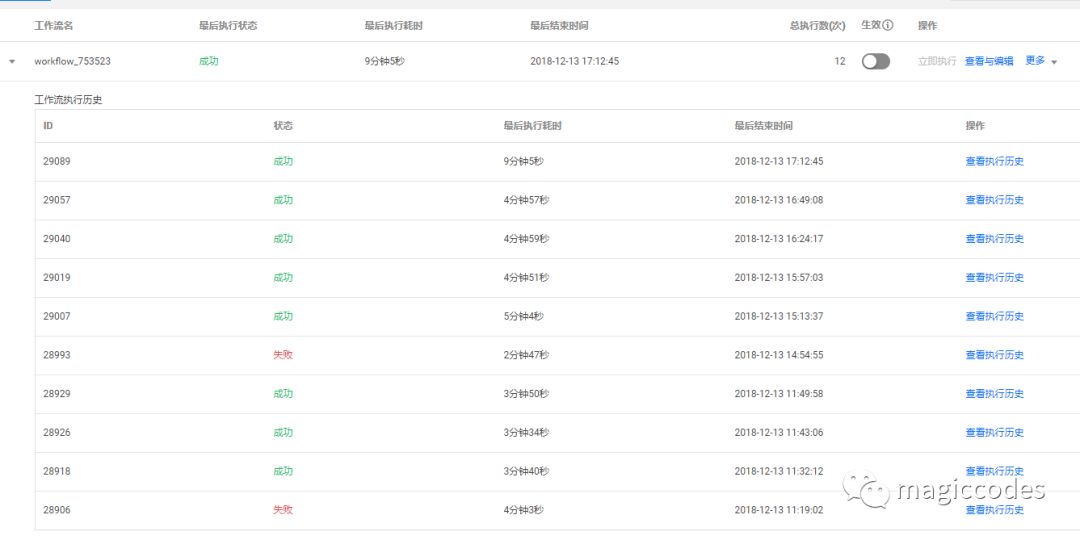
同时，还可以查看日志历史：

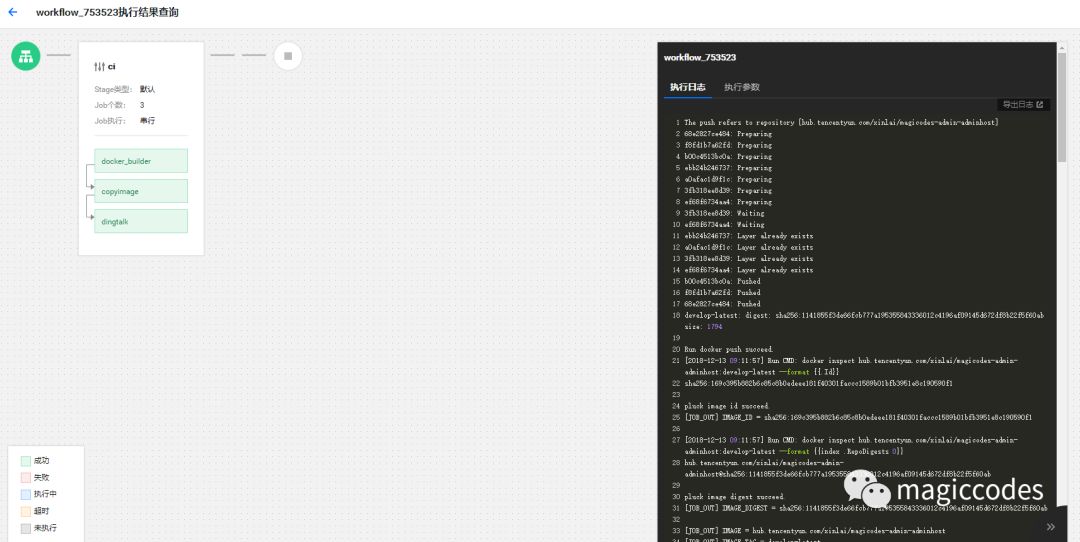
Tencent hub工作流我们就先介绍到这里。

其他配置

接下来，我们需要切到腾讯云的容器服务管理面板。此节内容因为前面教程讲述过，因此本节一笔带过。

首先我们需要创建集群并且添加节点：

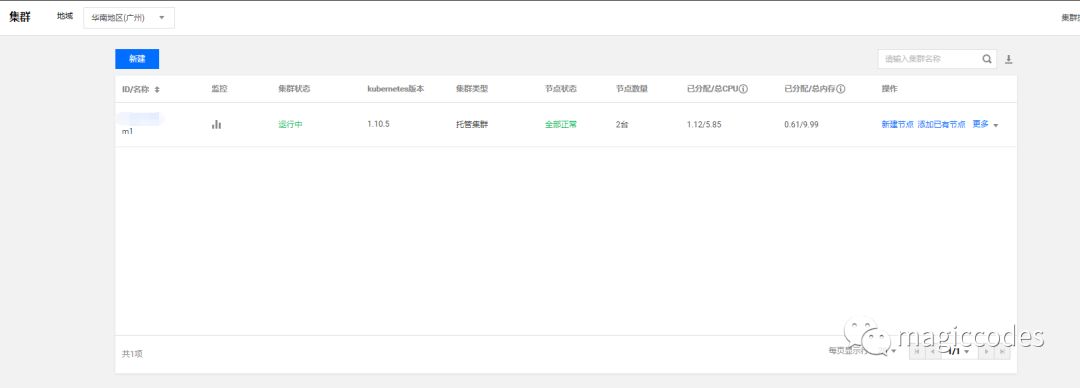
然后创建服务（我们可以基于镜像构建服务，也可以直接创建服务）：

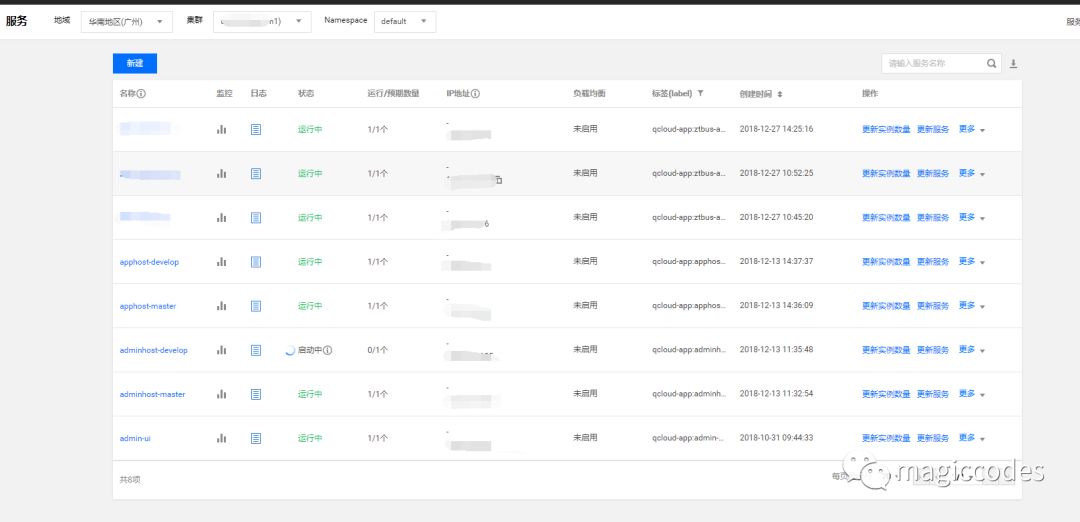
接下来，我们需要设置镜像触发器，如下所示：

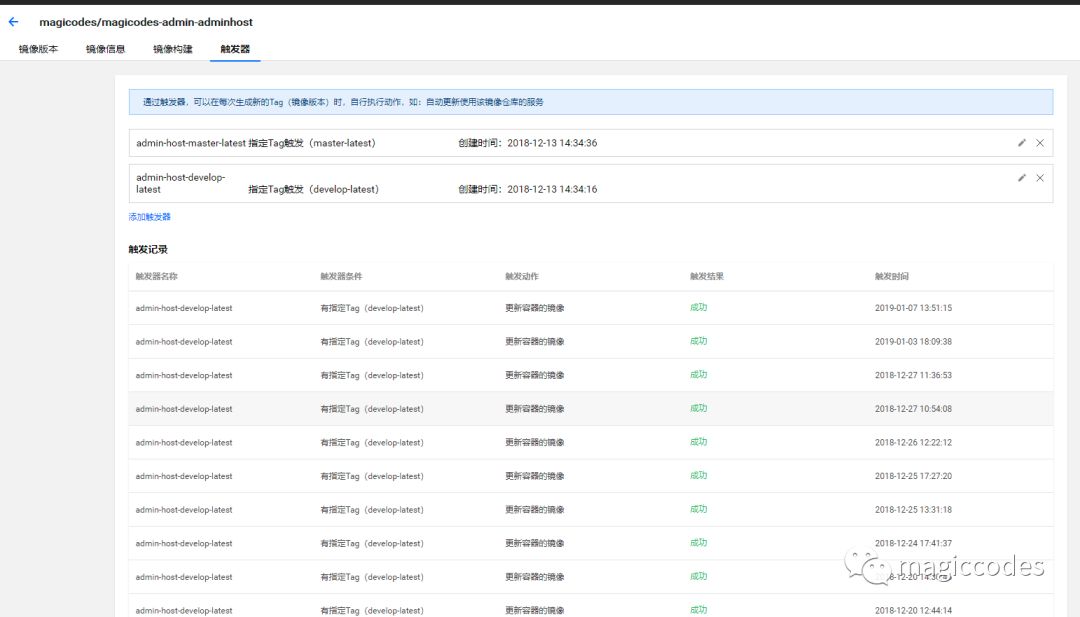
注意：我们可以通过不同的标签触发不同的服务更新，比如develop代表开发环境，master代表正式环境。

此节内容我们在前面的教程已经讲述过，这里就不赘述了。整个构建过程，我们可以添加一些webhook来进行消息集成，方便开发团队知晓相关情况以及测试人员进行测试。消息集成这块，我们再通过后续的教程来分享我们团队的消息集成，大家可以关注我们的公众号“magiccodes”来查看全部教程和文章。

转载是一种动力 分享是一种美德

如果喜欢作者的文章，请关注“magiccodes”订阅号以便第一时间获得最新内容。本文版权归作者和湖南心莱信息科技有限公司共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

QQ群：

编程交流群<85318032> 

产品交流群<897857351>

Docker最全教程——从理论到实战（一）

Docker最全教程——从理论到实战（二）

Docker最全教程——从理论到实战（三）

Docker最全教程——从理论到实战（四）

Docker最全教程——从理论到实战（五）

Docker最全教程——从理论到实战（六）

Docker最全教程——从理论到实战（七）

Docker最全教程——从理论到实战(八)    

Docker最全教程——从理论到实战（九）