确实没想到自己写文章能隔这么久，鸽王预警

T1:One-Dimensional

title

考虑一个含有 N 个细胞的一维细胞自动机。细胞从 0 到 N-1 标号。

每个细胞有一个被表示成一个小于 M 的非负整数的状态。细胞的状态会在每个整数时刻发生骤变。

我们定义 S(i,t) 表示第 i 个细胞在时刻 t 的状态。在时刻 t+1 的状态被表示为 S(i,t+1)=(A×S(i-1,t)+B×S(i,t)+C×S(i+1,t) ) mod M ，

其中 A,B,C 是给定的非负整数。对于 i<0 或 N≤i ，我们定义 S(i,t)=0 。

给定一个自动机的定义和其细胞在时刻 0 的初始状态，你的任务是计算时刻 T 时每个细胞的状态。

输入格式
输入包含多组测试数据。每组数据的第一行包含六个整数 N,M,A,B,C,T 。

第二行包含 N 个小于 M 的非负整数，依次表示每个细胞在时刻 0 的状态。输入以六个零作为结束。

输出格式
对于每组数据，输出N个小于M的非负整数，每两个相邻的数字之间用一个空格隔开，表示每个细胞在时刻T的状态。

样例
样例输入
5 4 1 3 2 0
0 1 2 0 1
5 7 1 3 2 1
0 1 2 0 1
5 13 1 3 2 11
0 1 2 0 1
5 5 2 0 1 100
0 1 2 0 1
6 6 0 2 3 1000
0 1 2 0 1 4
20 1000 0 2 3 1000000000
0 1 2 0 1 0 1 2 0 1 0 1 2 0 1 0 1 2 0 1
30 2 1 0 1 1000000000
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
30 2 1 1 1 1000000000
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
30 5 2 3 1 1000000000
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0
样例输出
0 1 2 0 1
2 0 0 4 3
2 12 10 9 11
3 0 4 2 1
0 4 2 0 4 4
0 376 752 0 376 0 376 752 0 376 0 376 752 0 376 0 376 752 0 376
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 3 2 2 2 3 3 1 4 3 1 2 3 0 4 3 3 0 4 2 2 2 2 1 1 2 1 3 0
数据范围与提示
$0<N\le 50,0<M\le 1000,0\le a,b,c<M,0\le t\le 10^9$

solution

其实是很裸的一个矩阵快速幂，当我们画出下面一组图的时候
脑子里面就因该出现矩阵的婀娜多姿 加速矩阵的美貌了


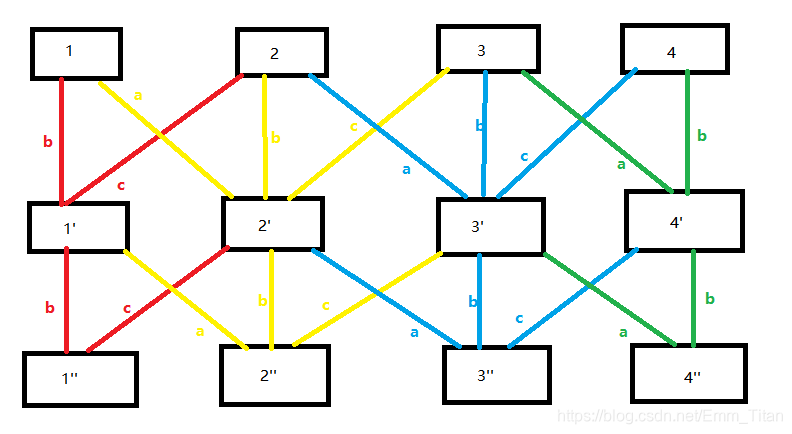
已经呼之欲出了，这里直接呈现(原矩阵是一行m列的加速矩阵，如果原矩阵是m行1列，请将加速矩阵沿左对角线一一对应交换（翻折）)
$$\left[\begin{array}{ccccc}b& 0& 0& ...& 0\\ c& a& 0& ...& 0\\ 0& b& a& ...& 0\\ 0& c& b& ...& 0\\ .& .& .& .& .\\ 0& 0& 0& ...& a\\ 0& 0& 0& ...& b\end{array}\right]$$

code

#include <cstdio>
#include <cstring>
using namespace std;
#define MAXN 55
#define LL long long
int mod, n, a, b, c, t;struct Matrix {int n, m;int c[MAXN][MAXN];Matrix () {memset ( c, 0, sizeof ( c ) );}Matrix operator * ( const Matrix &a ) {Matrix ans;ans.n = n;ans.m = a.m;for ( int i = 1;i <= n;i ++ )for ( int k = 1;k <= m;k ++ )if ( c[i][k] )for ( int j = 1;j <= a.m;j ++ )ans.c[i][j] = ( ans.c[i][j] + c[i][k] * a.c[k][j] % mod ) % mod;return ans;}}A, B;int main() {while ( scanf ( "%d %d %d %d %d %d", &n, &mod, &a, &b, &c, &t ) != EOF ) {if ( ! n && ! mod && ! a && ! b && ! c && ! t )return 0;memset ( A.c, 0, sizeof ( A.c ) );memset ( B.c, 0, sizeof ( B.c ) );A.n = 1, A.m = B.n = B.m = n;for ( int i = 1;i <= n;i ++ ) {scanf ( "%d", &A.c[1][i] );if ( i > 1 )B.c[i - 1][i] = a;B.c[i][i] = b;if ( i < n )B.c[i + 1][i] = c;}while ( t ) {if ( t & 1 )A = A * B;B = B * B;t >>= 1;}for ( int i = 1;i <= n;i ++ )printf ( "%d ", A.c[1][i] );printf ( "\n" );}return 0;
}

T2:【NOIP模拟赛】Freda的迷宫

title

Freda是一个迷宫爱好者，她利用业余时间建造了许多迷宫。每个迷宫都是由若干房间和走廊构成的，每条走廊都连接着两个不同的房间，两个房间之间最多只有一条走廊直接相连，走廊都是双向通过。
黄昏时候，Freda喜欢在迷宫当中漫步。每天，Resodo都会为Freda设计一个挑战方案。Resodo会指定起点和终点，请Freda来找到一条从起点到终点的简单路径。一条简单路径定义为一个房间序列，每个房间至多在序列里出现一次，且序列中相邻的两个房间有走廊相连。当起点和终点之间存在且仅存在一条简单路径的时候，Freda认为这个挑战方案是RD的。现在，请你帮帮Resodo来写一个程序，判断一个挑战方案是否是RD的。

输入格式
第一行三个整数N,M,Q.分别表示房间数，走廊数，询问数。
接下来M行每行2个整数x,y, 0<x,y<=N, 表示x和y之间有一条走廊相连。
接下来Q行每行2个整数x,y, 表示询问以x为起点,y为终点的挑战方案是否是RD的.

输出格式
对于每个询问，输出一行”Y”或者”N”（不含引号）.Y表示该询问所表示的挑战方案是RD的,N表示该询问所表示的挑战方案不是RD的.

样例
样例输入
6 5 3
1 2
2 3
2 4
2 5
4 5
1 3
1 5
2 6
样例输出
Y
N
N
数据范围与提示
样例解释
1,3之间只有一条路径 1->2->3
1,5之间有两条路径 1->2->5 ; 1->2->4->5
1,6之间没有路径
数据范围与约定
对于30%的数据，N<=100， M<=1000, Q<=100.
对于50%的数据，N<=1000, M<=10000, Q<=1000.
对于100%的数据，N<=10000, M<=100000, Q<=10000.

solution

这道题，也挺裸的，要不是我当时打爆了

其实就是把这一条路径抠出来，然后康康这上面是不是都是由简单路径组成的
因为两点之间有且仅有一条简单路径，所以路径上的边都是桥
若有不为桥的边，则一定可以找到另一条路径连接不为桥的边的两个结点。
因此我们可以用无向强连通分量跑出每一条桥，然后用并查集将其捆绑，最后直接判断两点是否在一个并查集里面就行了

code

#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
#define MAXN 10005
vector < int > G[MAXN];
int n, m, Q, cnt;
int f[MAXN], dfn[MAXN], low[MAXN];void MakeSet () {for ( int i = 1;i <= n;i ++ )f[i] = i;
}int FindSet ( int x ) {if ( x != f[x] )return f[x] = FindSet ( f[x] );return x;
}void UnionSet ( int u, int v ) {int fu = FindSet ( u ), fv = FindSet ( v );if ( fu != fv )f[fu] = fv;
}void tarjan ( int u, int fa ) {dfn[u] = low[u] = ++ cnt;for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( ! dfn[v] ) {tarjan ( v, u );low[u] = min ( low[u], low[v] );if ( low[v] > dfn[u] )UnionSet ( u, v );}else if ( dfn[u] > dfn[v] && v != fa )low[u] = min ( low[u], dfn[v] );}
}int main() {scanf ( "%d %d %d", &n, &m, &Q );for ( int i = 1;i <= m;i ++ ) {int x, y;scanf ( "%d %d", &x, &y );G[x].push_back ( y );G[y].push_back ( x );}MakeSet ();tarjan ( 1, 0 );for ( int i = 1;i <= Q;i ++ ) {int x, y;scanf ( "%d %d", &x, &y );if ( FindSet ( x ) == FindSet ( y ) )printf ( "Y\n" );elseprintf ( "N\n" );}return 0;
}

T3:【NOIP模拟赛】一道防AK好题

title

Lemon认为在第一届『Citric』杯模拟赛中出的题目太简单了，于是他决定，这次要给参赛选手们一个下马威！ ^_

Lemon手上有一个长度为n的数列，第i个数为xi。
他现在想知道，对于给定的a,b,c，他要找到一个i，使得$a\ast (i+1)\ast x{i}^2+(b+1)\ast i\ast xi+(c+i)=0$成立。
如果有多个i满足，Lemon想要最小的那个i。
Lemon有很多很多组询问需要你回答，多到他自己也不确定有多少组。所以在输入数据中a=b=c=0标志着Lemon的提问的结束。

更加糟糕的是，Lemon为了加大难度，决定对数据进行加密以防止离线算法的出现。
假设你在输入文件中读到的三个数为a0,b0,c0，那么Lemon真正要询问的a=a0+lastans,b=b0+lastans,c=c0+lastans.
lastans的值是你对Lemon的前一个询问的回答。如果这是第一个询问，那么lastans=0
所有的询问都将会按上述方式进行加密，包括标志着询问的结束的那个询问也是这样。

为提高读入效率，请用scanf()，而不能用cin，即使加sync_with_stdio(false)也不行！

对于不确定数量的数据，当读入完最后一行数据后，再次调用scanf()，会返回-1，以此可判断读入是否结束。

输入格式
输入文件第一行包含一个正整数n，表示数列的长度。
输入文件第二行包含n个整数，第i个数表示xi的值。
接下来若干行，每行三个数，表示加密后的a,b,c值（也就是上文所述的a0,b0,c0）

输出格式
包含若干行，第i行的值是输入文件中第i个询问的答案。注意，你不需要对标志着询问结束的那个询问作答。
同时，标志着询问结束的询问一定是输入文件的最后一行。也就是，输入文件不会有多余的内容。

样例
样例输入
5
-2 3 1 -5 2
-5 -4 145
-1 -6 -509
-9 -14 40
-3 -13 21
-3 -3 -3
样例输出
5
4
3
3
数据范围与提示
第一个询问中，真实的a=-5+0=-5，b=-4+0=-4，c=145+0=145（第一个询问中lastans=0）
带入发现，i=5时，-5*(5+1)*2^2+(-4+1)52+145+5=0，而其他的i均不符合条件。所以答案是5.
第二个询问中，真实的a=-1+5=4,b=-6+5=-1,c=-509+5=-504（lastans是上一个询问的答案的值，也就是5）
经带入发现，i=4时，$4\ast (4+1)\ast (-5{)}^2+(-1+1)\ast 4\ast (-5)+(-504)+4=0$，满足条件，而其他的i均不满足条件，所以答案是4.
同理，第三个询问中真实的a=-5,b=-10,c=44.答案i=3
第四个询问中真实的a=0,b=-10,c=24，答案i=3
第五个询问中真实的a=0,b=0,c=0，此时我们发现这是一个标志着结束的询问，这个询问我们无需作出回答。

对于40%的数据，满足N<=1000，需要作出回答的询问个数不超过1000.
对于100%的数据，满足N<=50000，需要作出回答的询问个数不超过500000，xi的绝对值不超过30000，解密后的a的绝对值不超过50000，解密后的b的绝对值不超过10^8
解密后的c的绝对值不超过10^18.

solution

如果当你康到有加密强制在线

一直抓住在线不放去思考一些$log$算法，那么恭喜你
你成功get到了出题者的心意，不仅为你点个赞，棒棒！！
其实这道题的突破点就是a=b=c=0标志着Lemon的提问的结束
也就是说最后的加密出来的$a,b,c$一定都为零，而我又知道每一次加密前的
$a0,b0,c0$为什么不搞点颜色呢

---

假设上一次的答案是$lastans$，这一次的答案是$ans$
那么一定满足$$(a+lastans)\ast (ans+1)\ast x_{ans}^2+(b+lastans+1)\ast ans\ast x_{ans}+ans+c=0$$
让我们对上面式子进行一些骚操作 化简
$$a\ast (ans+1)\ast x_{ans}^2+lastans\ast x_{ans}^2\ast (ans+1)+(b+1)\ast ans\ast x_{ans}+ans+c=0$$
$$lastans=-\frac{a\ast (ans+1)\ast x_{ans}^2+(b+1)\ast ans\ast x_{ans}+ans+c}{x_{ans}^2\ast (ans+1)+x_{ans}\ast ans+1}$$
利用这个递推式，我们可以先把所有输入都存下来，从最后一个已知答案开始往前推，就能离线之前所有答案搞定

code

#include <cstdio>
#define LL long long
#define MAXN 500005
int n, cnt;
LL a, b, c;
LL ans[MAXN], x[MAXN], A[MAXN], B[MAXN], C[MAXN];int main() {scanf ( "%d", &n );for ( int i = 1;i <= n;i ++ )scanf ( "%lld", &x[i] );while ( ~ scanf ( "%lld %lld %lld", &a, &b, &c ) )++ cnt, A[cnt] = a, B[cnt] = b, C[cnt] = c;ans[cnt - 1] = - A[cnt];	for ( int i = cnt - 1;i > 1;i -- ) {LL temp1 = A[i] * ( ans[i] + 1 ) * x[ans[i]] * x[ans[i]] + ( B[i] + 1 ) * ans[i] * x[ans[i]] + ans[i] + C[i];LL temp2 = x[ans[i]] * x[ans[i]] * ( ans[i] + 1 ) + x[ans[i]] * ans[i] + 1;ans[i - 1] = - temp1 / temp2;}for ( int i = 1;i < cnt;i ++ )printf ( "%lld\n", ans[i] );return 0;
}

家里的网速实在。。本来半个小时就搞定了，硬生生卡成了两小时

接下来要做常更得飞鸽王！！！