前言

终于出成绩了我可以写博客辣，官方数据还没出就先放洛谷的题目链接了。

---

正题

---

T1-廊桥分配

https://www.luogu.com.cn/problem/P7913

题目大意

有$m_1$种一类飞机，$m_2$种二类飞机，每个飞机有一个占用时间的区间。要给两类飞机分配恰好$n$个廊桥。
如果对于一类飞机当它来到时如果有空的它这一类的廊桥就会分配给他。
求最多能容纳多少飞机。

$1\le n\le 10^5,1\le m_1+m_2\le 10^5$

解题思路

因为飞机的策略就是能停就停，我们可以考虑贪心策略。
先考虑单类的飞机，假设分配的廊桥为$k$，当一辆飞机不能进入当且仅当现在$k$个廊桥已经被霸占了，此时如果需要停靠这俩飞机就需要新开一个廊桥。
我们可以设有无数个廊桥，然后我们优先分配编号小的廊桥，然后最后如果有$k$个廊桥时答案就是在$1\sim k$的廊桥排列的飞机数。
具体的做法对于两类各做一次，用一个优先队列维护现在所有被霸占的廊桥的恢复时间，然后用一个set维护现在空余的廊桥编号就可以了。

时间复杂度：$O(n\log n)$

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<queue>
#define mp(x,y) make_pair(x,y)
using namespace std;
const int N=1e5+10;
struct node{int l,r;
}a[N];
int n,m,f[N],g[N];set<int> s;
priority_queue<pair<int,int> > q;
bool cmp(node x,node y)
{return x.l<y.l;}
int main()
{int pm;scanf("%d%d%d",&n,&m,&pm);for(int i=1;i<=max(n,max(m,pm));i++)s.insert(i);for(int i=1;i<=m;i++)scanf("%d%d",&a[i].l,&a[i].r);sort(a+1,a+1+m,cmp);for(int i=1;i<=m;i++){while(!q.empty()&&-q.top().first<=a[i].l)s.insert(q.top().second),q.pop();int x=*s.begin();f[x]++;s.erase(x);q.push(mp(-a[i].r,x));}while(!q.empty())s.insert(q.top().second),q.pop();for(int i=1;i<=n;i++)f[i]+=f[i-1];m=pm;for(int i=1;i<=m;i++)scanf("%d%d",&a[i].l,&a[i].r);sort(a+1,a+1+m,cmp);for(int i=1;i<=m;i++){while(!q.empty()&&-q.top().first<=a[i].l)s.insert(q.top().second),q.pop();int x=*s.begin();g[x]++;s.erase(x);q.push(mp(-a[i].r,x));}while(!q.empty())s.insert(q.top().second),q.pop();for(int i=1;i<=n;i++)g[i]+=g[i-1];int ans=0;for(int i=0;i<=n;i++)ans=max(ans,f[i]+g[n-i]);printf("%d\n",ans);return 0;
}

---

T2-括号序列

https://www.luogu.com.cn/problem/P7914

题目大意

一个合格的括号序被定义为

然后给出带$\ast ,(,),?$的字符串，然后求有多少种把$?$切换成$(,),\ast$的方案使得是一个合法的括号序。
$1\le k\le n\le 500$

解题思路

开始考虑一个一个填发现不行。
然后这个复杂度考虑区间$dp$，设$f_{l,r}$表示区间$l\sim r$合法的方案。
然后考虑怎么转移，先维护一个$s_{l,r}$表示$l\sim r$是否能够凑成一个长度不超过$k$的全$\ast$序列。
对于第$1$种和第$3$种情况，先看下$l,r$是否能是${}^{\prime }{(}^{\prime }$和${}^{\prime }{)}^{\prime }$的形式，然后第一种情况就直接加$s_{l+1,r-1}+f_{l+1,r-1}$（对应$S/A$），第三种我们可以枚举$k\in [l+1,r-1)$，然后转移$f_{l+1,k}\times s_{k+1,r}+s_{l+1,k}\times f_{k+1,r}$（对应了$AS/SA$）就好了。
第$2$种情况比较麻烦，我们需要枚举一个$l\le L<R\le r$然后中间填$S$，就是$f_{l,L}\times f_{R,r}\times s_{L+1,R-1}$。但是这个枚举比较慢，因为对于一个$r$，满足$s_{l,r}=1$的$l$肯定是一个到$r$的区间，并且$r$向右移动时这个区间也向右移动，所以可以使用一个前缀和优化。

发现这样还是过不了样例，问题出在如果存在$ASASA$的情况，此时会被统计两次（$|ASA|SA$和$AS|ASA|$各一次），更多的同理，所以我们可以设$g_{l,r}$表示不带情况二时的合法方案，然后在后面转移就好了。

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const ll N=510,P=1e9+7;
ll n,k,f[N][N],g[N][N],S[N][N];char s[N];
signed main()
{scanf("%lld%lld",&n,&k);scanf("%s",s+1);for(ll i=1;i<=n;i++){S[i][i-1]=1;for(ll j=i;j<=min(n,i+k-1);j++){S[i][j]=S[i][j-1]&(s[j]=='?'||s[j]=='*');if(!S[i][j])break;}}for(ll len=2;len<=n;len++)for(ll l=1;l<=n-len+1;l++){ll r=l+len-1;if((s[l]=='?'||s[l]=='(')&&(s[r]=='?'||s[r]==')')){(f[l][r]+=S[l+1][r-1]+f[l+1][r-1])%=P;for(ll k=l+1;k<r-1;k++)(f[l][r]+=f[l+1][k]*S[k+1][r-1]+f[k+1][r-1]*S[l+1][k])%=P;}ll sum=0,z=l;g[l][r]=f[l][r];for(ll k=l;k<r;k++){(sum+=f[l][k])%=P;while(!S[z+1][k])(sum-=f[l][z])%=P,z++;(f[l][r]+=g[k+1][r]*sum%P)%=P;}}printf("%lld\n",(f[1][n]+P)%P);return 0;
}

---

T3-回文

https://www.luogu.com.cn/problem/P7915

题目大意

有一个长度为$2n$的序列$a$，保证$1\sim n$都各出现了两次，你有两种操作

• 将$a$的开头添加到序列$b$的末尾并在$a$移除。
• 将$a$的末尾添加到序列$b$的末尾并在$a$移除。

一操作为$L$，二操作为$R$，要求使得最终$b$回文的情况下操作序列的字典序最小。

$1\le T\le 100,\sum n\le 5\times 10^5$

解题思路

显然第一个丢进$b$的肯定是第一个或者最后一个，我们先假设是第一个且数字为$x$，那么最后被丢进去的肯定是另一个$x$。

然后我们可以从这个$x$的位置开始作为一个区间，然后开始每次你丢进去的下一个数都必须在这个区间的左右，然后再用这个区间再扩展丢进去的数的另一个的对应位置。

但是这样暴力搜丢左边还是右边是$2^n$的显然不行，但是我们发现假设如果一个情况左右都能丢，在字典序最小的情况下我们肯定是先丢左边的，而此时丢了之后不会导致右边不能丢了，所以此时丢左边肯定是最优的。

所以其实这样搜是$O(n)$的，时间复杂度$O(\sum n)$。

code

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int T,n,flag,a[N];char v[N];
void dfs(int d,int l,int r,int L,int R){if(l<L&&r>R){flag=1;for(int i=1;i<=2*n;i++)putchar(v[i]);putchar('\n');return;}if(d>n)return;if(L<=l&&(a[L]==a[l]&&L<l||a[L]==a[r]&&r<=R)){v[d]='L';if(a[L]==a[l]&&L<l)v[2*n-d+1]='L',dfs(d+1,l-1,r,L+1,R);else v[2*n-d+1]='R',dfs(d+1,l,r+1,L+1,R);}else if(r<=R&&(a[R]==a[l]&&L<=l||a[R]==a[r]&&r<R)){v[d]='R';if(a[R]==a[l]&&L<=l)v[2*n-d+1]='L',dfs(d+1,l-1,r,L,R-1);else v[2*n-d+1]='R',dfs(d+1,l,r+1,L,R-1);}return;
}
int main()
{scanf("%d",&T);while(T--){scanf("%d",&n);v[2*n]='L';flag=0;for(int i=1;i<=2*n;i++)scanf("%d",&a[i]);for(int i=2;i<=2*n;i++)if(a[i]==a[1]){v[1]='L';dfs(2,i-1,i+1,2,2*n);break;}if(flag)continue;for(int i=1;i<2*n;i++)if(a[i]==a[2*n]){v[1]='R';dfs(2,i-1,i+1,1,2*n-1);break;}if(flag)continue;puts("-1");}return 0;
}

---

T4-交通规划

https://www.luogu.com.cn/problem/P7916

题目大意

有一个$n$条水平线和$m$条垂直线交叉形成$n\times m$个格点的图，把所有的边按照顺时针排序如图。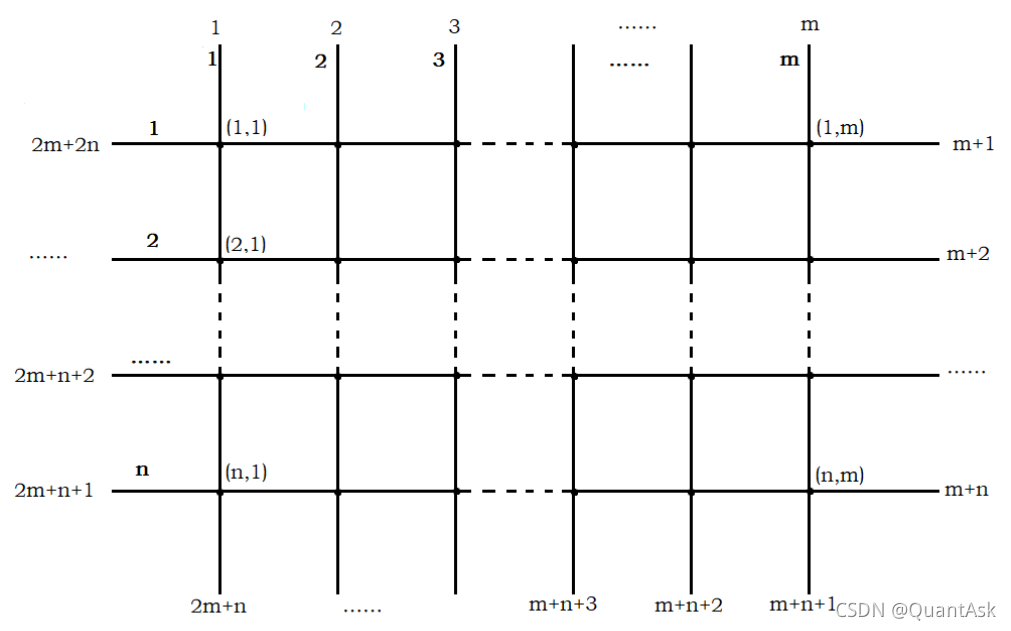
每个格点之间有边权。
$T$次询问，每次给出线外的$k$个额外点的位置，颜色（黑白），和连接线内边界格点的边权。

要求给网格上的所有点染色，要求使得两端颜色不同的边权值和最小。

$1\le T\le 50,\sum k\le 50,2\le n,m\le 500$。

解题思路

黑白染色求最小的权值其实就是为最小割，然后平面图最小割是可以转换成对偶图的最短路的。

显然的对于$k=2$的部分分就是直接求黑色额外点（如果颜色都相同显然答案为$0$）左右的对偶点在对偶图上的最短路。

对于$k$更大的情况我们具体分析一下对于下图的情况（为了好看用了红蓝代替黑白）

我们有两种割法（绿/黄）

发现其实可以写成四个点相互匹配的过程，由于产生交叉的肯定不优（通过改变匹配方式使得交叉部分消去），所以匹配的贡献可以直接写成最短路。

然后考虑如何找到优的匹配方案，我们可以把顺时针的和逆时针的匹配，因为如果顺顺-逆逆的匹配的话，肯定会产生交叉。（虽然这样匹配也可能产生交叉，但是因为权值不优所以不会影响答案）

然后就是一个二分图最大权值匹配的问题了，写个费用流就可以了。

虽然再利用交叉性质做环形区间$dp$也能过，但是我不会/kk

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cctype>
#include<vector>
#include<queue>
#define ll long long
#define mp(x,y) make_pair(x,y)
using namespace std;
const ll N=510,M=N*N,K=110;
struct edge{ll to,next,w;
}a[M<<2];
struct node{ll w,p,t;
}q[K];
ll n,m,T,tot,ls[M],f[M],wz[N<<2];
vector<int> A,B;bool v[M];
priority_queue<pair<ll,ll> > qt;
ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-')f=-f;c=getchar();}while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}return x*f;
}
struct Netflow{struct node{ll to,next,w,c;}a[K*K*2];ll tot=1,s=1,t=2,ans,ls[K],f[K],mf[K],pre[K];bool v[K];priority_queue<int> q;void clr(){tot=1;ans=0;memset(ls,0,sizeof(ls));return;}void addl(ll x,ll y,ll w,ll c){a[++tot].to=y;a[tot].next=ls[x];ls[x]=tot;a[tot].w=w;a[tot].c=c;a[++tot].to=x;a[tot].next=ls[y];ls[y]=tot;a[tot].w=0;a[tot].c=-c;return;}bool SPFA(){memset(f,0x3f,sizeof(f));q.push(s);f[s]=0;v[s]=1;mf[s]=1e9;while(!q.empty()){ll x=q.top();q.pop();v[x]=0;for(ll i=ls[x];i;i=a[i].next){ll y=a[i].to;if(a[i].w&&f[x]+a[i].c<f[y]){f[y]=f[x]+a[i].c;pre[y]=i;mf[y]=min(mf[x],a[i].w);if(!v[y])q.push(y),v[y]=1;}}}return (f[t]!=f[0]);}void Updata(){ll x=t;ans+=mf[t]*f[t];while(x!=s){a[pre[x]].w-=mf[t];a[pre[x]^1].w+=mf[t];x=a[pre[x]^1].to;}return;}ll GetAns(){while(SPFA())Updata();return ans;}
}Nt;
ll p(ll x,ll y)
{return x*(m+1)+y;}
void addl(ll x,ll y,ll w){a[++tot].to=y;a[tot].next=ls[x];ls[x]=tot;a[tot].w=w;a[++tot].to=x;a[tot].next=ls[y];ls[y]=tot;a[tot].w=w;return;
}
void dij(ll s){memset(f,0x3f,sizeof(f));memset(v,0,sizeof(v));f[s]=0;qt.push(mp(0,s));while(!qt.empty()){ll x=qt.top().second;qt.pop();if(v[x])continue;v[x]=1;for(ll i=ls[x];i;i=a[i].next){ll y=a[i].to;if(f[x]+a[i].w<f[y]){f[y]=f[x]+a[i].w;qt.push(mp(-f[y],y));}}}return;
}
ll getp(ll x,ll f){if(x<=m)return p(0,x+f);if(x<=m+n)return p(x-m+f,m);if(x<=2*m+n)return p(n,m-(x-m-n+f));return p(n-(x-2*m-n+f),0);
}
bool cmp(node x,node y)
{return x.p<y.p;}
signed main()
{n=read();m=read();T=read();for(ll i=1;i<n;i++)for(ll j=1;j<=m;j++){ll w=read();addl(p(i,j-1),p(i,j),w);}for(ll i=1;i<=n;i++)for(ll j=1;j<m;j++){ll w=read();addl(p(i-1,j),p(i,j),w);}for(ll i=1;i<=m;i++)addl(p(0,i-1),p(0,i),0),wz[i]=tot;for(ll i=1;i<=n;i++)addl(p(i-1,m),p(i,m),0),wz[i+m]=tot;for(ll i=1;i<=m;i++)addl(p(n,m-i+1),p(n,m-i),0),wz[i+n+m]=tot;for(ll i=1;i<=n;i++)addl(p(n-i+1,0),p(n-i,0),0),wz[i+n+2*m]=tot;while(T--){ll k=read();Nt.clr();A.clear();B.clear();for(ll i=1;i<=k;i++){q[i].w=read();q[i].p=read();q[i].t=read();a[wz[q[i].p]].w=a[wz[q[i].p]-1].w=q[i].w;}sort(q+1,q+1+k,cmp);q[0]=q[k];q[k+1]=q[1];for(ll i=1;i<=k;i++)if(q[i].t==1&&q[i-1].t==0)A.push_back(getp(q[i].p,-1));for(ll i=1;i<=k;i++)if(q[i].t==1&&q[i+1].t==0)B.push_back(getp(q[i].p,0));for(ll i=0;i<A.size();i++){Nt.addl(1,3+i,1,0);dij(A[i]);for(ll j=0;j<B.size();j++)Nt.addl(3+i,3+A.size()+j,1,f[B[j]]);}for(ll i=0;i<B.size();i++)Nt.addl(3+A.size()+i,2,1,0);printf("%lld\n",Nt.GetAns());for(ll i=1;i<=k;i++)a[wz[q[i].p]].w=a[wz[q[i].p]-1].w=0;}return 0;
}