搜索与回溯讲解

深搜

DFS
一股莽到底，然后再找下一个，如果无法拓展，则退回一步到上一个状态，再按照原先设定的规则顺序重新寻找一个状态拓展。
例子：走迷宫，不走到路的尽头不回头

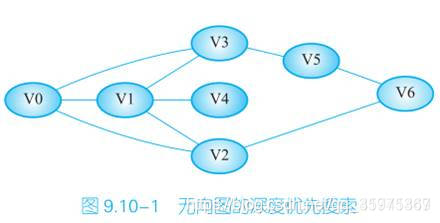
得到的序列：V0，V1，V2，V6，V5，V3，V4
代码：

void dfs(int dep, 参数表 );{自定义参数 ;if( 当前是目标状态 ){输出解或者作计数、评价处理 ;}elsefor(i = 1; i <= 状态的拓展可能数 ; i++)if( 第 i 种状态拓展可行 ){维护自定义参数 ;dfs(dep+1, 参数表 );}
}

回溯：
“回溯法”也称“试探法”。它是从问题的某一状态出发，不断“试探”着往前走一步，当一条路走到“尽头”，不能再前进（拓展出新状态）的时候，再倒回一步或者若干步，从另一种可能的状态出发，继续搜索，直到所有的“路径（状态）”都一一试探过。这种不断前进、不断回溯，寻找解的方法，称为“回溯法”。

void search(int dep){自定义参数 ;if( 当前是目标状态 ){输出解或者作计数和评价处理 ;}elsefor(i = 1; i <= 状态的拓展可能数 ; i++)if( 第 i 种状态拓展可行 ){保存现场 ( 断点 ), 维护自定义参数 ;search(dep+1);恢复现场 , 回溯到上一个断点继续执行 ;}
}

深度优先搜索可以采用递归（系统栈）和非递归（手工栈）两种方法实现

方向向量：

int dir[4][2]= {0,1,0,-1,1,0,-1,0}; // 方向向量，(x,y)周围的四个方向
-------
int dx[]={1,0,-1,0}
int dy[]={0,1,0,-1}

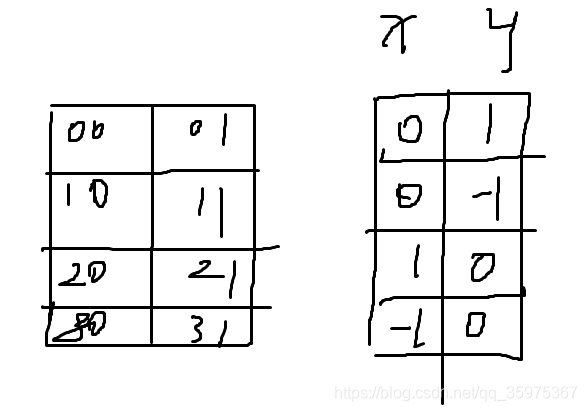
DFS代码：

/*
该DFS 框架以2D 坐标范围为例，来体现DFS 算法的实现思想。
*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
using namespace std;
const int maxn=100;
bool vst[maxn][maxn]; // 访问标记
int map[maxn][maxn]; // 坐标范围
int dir[4][2]= {0,1,0,-1,1,0,-1,0}; // 方向向量，(x,y)周围的四个方向
bool CheckEdge(int x,int y) { // 边界条件和约束条件的判断if(!vst[x][y] && ...) // 满足条件return 1;else // 与约束条件冲突return 0;
}
void dfs(int x,int y) {vst[x][y]=1; // 标记该节点被访问过if(map[x][y]==G) { // 出现目标态G...... // 做相应处理return;}for(int i=0; i<4; i++) {if(CheckEdge(x+dir[i][0],y+dir[i][1])) // 按照规则生成下一个节点dfs(x+dir[i][0],y+dir[i][1]);}return; // 没有下层搜索节点，回溯
}
int main() {......return 0;
}

题目讲解：

八皇后问题

在国际象棋棋盘上（8*8）放置八个皇后，使得任意两个皇后之间不能在同一行，同一列，也不能位于同于对角线上。问共有多少种不同的方法，并且按字典序从小到大指出各种不同的放法。

思路：
枚举1～N的全排列，每列举完一组，然后就在该组排列中测试当前方案是否合法（排列中每个元素与该排列中其他的元素不在横、竖、斜线上）
代码：

#include <cstdio>
#include <cstdlib>const int MAXN = 100;
int N;
bool hashTable[MAXN]  = {false};
int P[MAXN];
int count = 0;void DFS(int index){//朴素算法if(index == N + 1){bool flag = true;//flag为true，表示当前方案合法for (int i = 1; i <= N ; ++i)//遍历两个皇后，{for (int j = i + 1; j <= N; ++j){//第四象限内，P[y]为纵坐标，i、j为横坐标if(abs(i - j) == abs(P[j] - P[i])){//如果在一条对角线上，也就是正方形相对的两个端点flag = false;}}}if(flag == true) {count++;for (int i = 1; i <= N; ++i){printf("%d", P[i]);if(i <= N - 1) printf(" ");}printf("\n");}}for (int i = 1; i <= N; ++i)//全排列{if(hashTable[i] == false){P[index] = i;hashTable[i] = true;DFS(index + 1);hashTable[i] = false;}}
}int main(){scanf("%d", &N);DFS(1);if(count == 0) printf("no solute!\n");return 0;
}

字符序列

题目描述

从三个元素的集合[A，B，C]中选取元素生成一个 N 个字符组成的序列，使得没有两个相邻的子序列（子序列长度=2）相同。例：N = 5 时 ABCBA 是合格的，而序列 ABCBC 与 ABABC 是不合格的，因为其中子序列 BC，AB 是相同的。
对于由键盘输入的 N(1<=N<=12)，求出满足条件的 N 个字符的所有序列和其总数。

思路：
依旧靠模拟现在数组中的元素并且判断相邻两个
元素构成的子序列是否是满足条件的解，是就进行
计数并搜索下一层

代码：

#include<cstdio>
#define ll long long
ll a[1000005],n,sum;
bool check(int p)
{return p>3&&a[p-3]*10+a[p-2]==a[p-1]*10+a[p];
}
void dfs(int p)
{ll i;//要每次都重新定义i的变量，不然在调用的时候会改变外层搜索的i变量 for(i=1;i<=3;i++){a[p]=i;if(check(p))//只用判断相邻的字符串，之前的是因为判断了所有的情况 continue;else{if(p==n)sum++;elsedfs(p+1);}}
}
int main()
{scanf("%lld",&n);dfs(1);printf("%lld",sum);
}

自然数的拆分

题目描述：

任何一个大于1的自然数n，总可以拆分成若干个小于n的自然数之和。
当n=7共14种拆分方法：
7=1+1+1+1+1+1+1
7=1+1+1+1+1+2
7=1+1+1+1+3
7=1+1+1+2+2
7=1+1+1+4
7=1+1+2+3
7=1+1+5
7=1+2+2+2
7=1+2+4
7=1+3+3
7=1+6
7=2+2+3
7=2+5
7=3+4

输入一个n，按字典序输出具体的方案。

输入样例
7
输出样例
1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4

题解：
层层分解，按照dfs的顺序进行

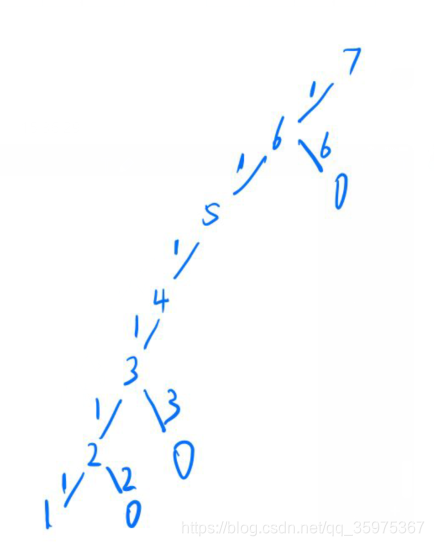
代码：

#include<cstdio>
int a[1005]={1},n;
int print(int t)
{int i;for(i=1;i<t-1;i++)printf("%d+",a[i]);if(a[t-1]!=n)printf("%d\n",a[t-1]);
}
int search(int s,int t)
{int i;if(s==0)print(t);for(i=a[t-1];i<=s;i++){a[t]=i;search(s-i,t+1);}
}
int main()
{scanf("%d",&n);search(n,1);
}

广搜

BFS
应用产生式规则和控制策略生成多层结点
广搜是扩散式的
例子：眼镜掉在地上，趴在地板上找，一开始先搜最接近的地方，如果没有再摸远一点的地方，距离依次增加

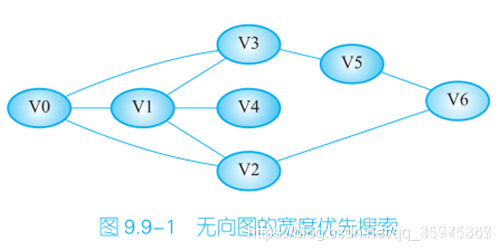
得到的一个序列为 V0，V1，V2，V3，V4，V6，V5。
宽度优先搜索是一种“盲目”搜索，所有结点的拓展都遵循“先进先出”的原则，所以采用“队列”来存储这些状态。宽度优先搜索的算法框架如下：

void BFS{while (front <= rear){// 当队列非空时做，front 和 rear 分别表示队列的头指针和尾指针      if (找到目标状态)做相应处理(如退出循环输出解、输出当前解、比较解的优劣);else{拓展头结点 ;if( 拓展出的新结点没出现过 ){rear++;将新结点插到队尾 ;}}front++;// 取下一个结点}
}

BFS代码：

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int maxn = 100;
bool vst[maxn][maxn]; // 访问标记
int dir[4][2] = {0,1,0,-1,1,0,-1,0}; // 方向向量
struct State { // BFS 队列中的状态数据结构int x, y; // 坐标位置int Step_Counter; // 搜索步数统计器
};
State a[maxn];
bool CheckState(State s) { // 约束条件检验if(!vst[s.x][s.y] && ...) // 满足条件return 1;else // 约束条件冲突return 0;
}
void bfs(State st) {queue <State> q; // BFS 队列State now, next; // 定义2 个状态，当前和下一个st.Step_Counter = 0; // 计数器清零q.push(st); // 入队vst[st.x][st.y] = 1; // 访问标记while(!q.empty()) {now = q.front(); // 取队首元素进行扩展if(now == G) { // 出现目标态，此时为Step_Counter 的最小值，可以退出即可...... // 做相关处理return;}for(int i = 0; i < 4; i++) {next.x = now.x + dir[i][0]; // 按照规则生成下一个状态next.y = now.y + dir[i][1];next.Step_Counter = now.Step_Counter+1; // 计数器加1if(CheckState(next)) { // 如果状态满足约束条件则入队q.push(next);vst[next.x][next.y] = 1; //访问标记}}q.pop(); // 队首元素出队}return;
}
int main() {......return 0;
}

题目讲解：

瓷砖

在一个 w×h 的矩形广场上，每一块 1×1 的地面都铺设了红色或黑色的瓷砖。小林同学站在某一块黑色的瓷砖上，他可以从此处出发，移动到上、下、左、右四个相邻的且是黑色的瓷砖上。现在，他想知道，通过重复上述移动所能经过的黑色瓷砖数。

样例：

样例输入
11 9
. # . . . . . . . . .
. # . # # # # # # # .
. # . # . . . . . # .
. # . # . # # # . # .
. # . # . . @ # . # .
. # . # # # # # . # .
. # . . . . . . . # .
. # # # # # # # # # .
. . . . . . . . . . .
样例输出
59

题解：
找到小林的初始位置“@”，并把坐标入队，作为队头元素。宽度优先搜索，检查队头元素的上、下、左、右四个位置是否是黑色瓷砖“.”，是则入队，……不断取出队头元素进行四个方向的拓展，直到队列为空。
为了避免一个位置被多次重复走到，定义一个布尔型数组 vis[i,j]用来判重，位置（i，j）为黑色瓷砖设置为 true，红色的或者走过的瓷砖设置为 false
最后队列内元素数量
在本题中其实还牵扯一个应用：联通块
代码：

#include<iostream>
#include<queue>
using namespace std;const int N = 25;
char map[N][N];
int n, m;
int dx[] = {1, 0, -1, 0}, dy[] = {0, 1, 0 , -1};
int ans;// 判断 (x, y) 是否在地图中
bool inmap(int x, int y) {return x >= 0 && x < m && y >= 0 && y < n;
}void bfs(int x, int y) {queue<pair<int, int>> q;// 首先将当前位置改为 '#' 表示已经走过了map[x][y] = '#';// 将x, y加入到队列中q.push({x, y});while (!q.empty()) {// 取出队列的头结点pair<int, int> xy = q.front();q.pop();// 向4个方向拓展for (int i = 0; i < 4; i++) {int x1 = xy.first + dx[i], y1 = xy.second + dy[i];// 如果下一个要走的点在地图内并且为黑色砖块，那么就将该点改为 '#' 并加入到队列中if (inmap(x1, y1) && map[x1][y1] == '.') {q.push({x1, y1});map[x1][y1] = '#';ans++;}}}
}int main() {// 输入 n 列 m 行cin >> n >> m;while (n != 0  && m != 0) {for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {cin >> map[i][j];}}queue<pair<int, int>> p;// 找到开始的地点int x, y;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (map[i][j] == '@') {x = i;y = j;break;}}}// bfs// 每次将 ans 初始化为 1，因为出发点算一个ans = 1;bfs(x, y);cout << ans << endl;cin >> n >> m;}return 0;
}

关系网络

描述
有N个人，编号为1到N，其中有一些人互相认识，现在x想认识y,可以通过他所认识的人来认识更多的人
如果x认识y,y认识z,则x可以通过y来认识z,求出x最少需要通过多少人才能认识y

输入
5 1 5
0 1 0 0 0
1 0 1 1 0
0 1 0 1 0
0 1 1 0 1
0 0 0 1 0
输出：
2

思路：
典型的BFS，直接搜就行了，最后输出时记得减一，因为要到达的人自己不算。
代码：

#include<bits/stdc++.h>
using namespace std;
int n,x,y;
struct node{int num;//编号 int t;//步数 node(){}node(int sum,int tt){num=sum;t=tt;}
};
int mp[101][101];//图 
bool flag[101];//标记 
queue<node> q;
void bfs()
{q.push(node(x,0));flag[x]=true;//打标记 while(!q.empty()){node head=q.front();q.pop();if(head.num==y){cout<<head.t-1;//一定要减一 return;}for(int i=1;i<=n;i++){if(mp[head.num][i]&&!flag[i]){flag[i]=true;q.push(node(i,head.t+1));}}}}int main(){cin>>n>>x>>y;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>mp[i][j];//存图 }}bfs();
}

bfs与dfs的用途与区别

1.BFS是用来搜索最短径路的解是比较合适的，比如求最少步数的解，最少交换次数的解，因为BFS搜索过程中遇到的解一定是离根最近的，所以遇到一个解，一定就是最优解，此时搜索算法可以终止。这个时候不适宜使用DFS，因为DFS搜索到的解不一定是离根最近的，只有全局搜索完毕，才能从所有解中找出离根的最近的解。（当然这个DFS的不足，可以使用迭代加深搜索ID-DFS去弥补）
2.空间优劣上，DFS是有优势的，DFS不需要保存搜索过程中的状态，而BFS在搜索过程中需要保存搜索过的状态，而且一般情况需要一个队列来记录。
3.DFS适合搜索全部的解，因为要搜索全部的解，那么BFS搜索过程中，遇到离根最近的解，并没有什么用，也必须遍历完整棵搜索树，DFS搜索也会搜索全部，但是相比DFS不用记录过多信息，所以搜素全部解的问题，DFS显然更加合适。

搜索剪枝

常用的搜索有Dfs和Bfs。

Bfs的剪枝通常就是判重，因为一般Bfs寻找的是步数最少，重复的话必定不会在之前的情况前产生最优解。

深搜，它的进程近似一颗树(通常叫Dfs树)。

而剪枝就是一种生动的比喻：把不会产生答案的，或不必要的枝条“剪掉”。

剪枝的关键就在于剪枝的判断：什么枝该剪，什么枝不该剪，在什么地方减。
正确性，准确性，高效性。

常用的剪枝有：可行性剪枝、最优性剪枝、记忆化搜索、搜索顺序剪枝。

可行性剪枝

如果当前条件不合法就不再继续搜索，直接return。这是非常好理解的剪枝

最优性剪枝

如果当前条件所创造出的答案必定比之前的答案大，那么剩下的搜索就毫无必要，甚至可以剪掉。

我们利用某个函数估计出此时条件下答案的‘下界’，将它与已经推出的答案相比，如果不比当前答案小，就可以剪掉。

比如：
在搜索取和最大值时，如果后面的全部取最大仍然不比当前答案大就可以返回。
在搜和最小时同理，可以预处理后缀最大/最小和进行快速查询。

long long ans=987474477434487ll;
... Dfs(int x,...)
{if(x... && ...){ans=....;return ...;}if(check2(x)>=ans)return ...;	//最优性剪枝 for(int i=1;...;++i){vis[...]=1; dfs(...);vis[...]=0;}
}

记忆化搜索

（之后dp会讲）

搜索顺序剪枝

在一些迷宫题，网格题，或者其他搜索中可以贪心的题，搜索顺序显得十分重要
其实在迷宫、网格类的题目中，以左上->右下为例，右下左上就明显比左上右下优秀。

题目：

[NOIP2002 提高组] 字串变换

题目描述：
给字符串A和B，然后给出最多6个变换规则：
A1 -> B1
问A能否变成B

输入
abcd xyz
abc xu
ud y
y yz

3

题解：
题目一共就6个变换规则，而且问最少步数，基本上就锁定是广搜，不仅可以寻找解而且还能判断步数
起点为a串，搜索目标为b串，中间的路径是给出的变换关系
我们用一个map来记录某个串是否被搜索过
对于串str，我们从第i为看是否能用第j种手段改变，如果拼接出的串是合法的，那么我们就把这个串继续压入队列，再次搜索，中间记录一下步数step和ans。
代码：

#include<bits/stdc++.h>     //万能头文件
using namespace std;
string a,b;                 //字符串A与字符串B
string sa[8],sb[8];         //存放6种转换方式
map<string,int> map1;       //用map存放已经宽搜过的字符串，用来判重剪枝（否则会超时）
int l;                      //有l种转换方式
queue<string> q;            //存放转换出来的字符串
queue<int> bb;              //存放当前转换出来的字符串已经使用的步数
int bfs()
{int i,j,k,m,n;string s,ss;while (q.empty()==0&&q.front()!=b&&bb.front()<=10)      //当还能继续转换且没转换出字符串B且步数也没有超出10步时进行宽搜{if (map1[q.front()]==1)         //剪枝：如果当前字符串已经宽搜过了,就弹出,进入下一次循环.{q.pop();bb.pop();continue;}map1[q.front()]=1;              //记录下该字符串for (i=1;i<=l;i++)              //循环出每一种转换方式{   s=q.front();                //将S赋值为当前要操作的字符串while (1)                   //找出子串sa[i]的所有位置{   m=s.find(sa[i]);        //在S里查找子串sa[i]的第一次出现位置if (m==-1) break;       //如果全找出来(找不到)了,就结束循环ss=q.front();           //将SS赋值为当前要操作的字符串ss.replace(m,sa[i].size(),sb[i]);   //在SS中用子串sb[i]替换掉S里第一次出现的子串sa[i]q.push(ss);             //将转换后的SS压入队列bb.push(bb.front()+1);  //将转换后的SS已经使用的步数压入队列s[m]='~';              //将S里子串sa[i]的第一次出现位置随便换成另一种无关的字符,//这样就可以查找到S里子串sa[i]的下一个出现位置}}q.pop();                        //将操作过的字符串弹出队列bb.pop();                       //操作过的字符串已经用过的步数一块弹出}if (q.empty()==1||bb.front()>10) return -1;//没法再进行宽搜,或者超出步数,就返回-1else return bb.front();                 //否则,就是找到了,便返回最少使用步数
}
int main()
{int i,j,k,m,n;cin>>a>>b;                          //读入字符串A与字符串Bl=1;while (cin>>sa[l]>>sb[l]) l++;      //读入转换方式l--;                                //l初始值为1,所以要减1,才能表示转换方式的数量if (l==0&&a!=b)                     //若果没有转换方式且A也不等于B,直接输出"NO ANSWER!"(其实这步可以不要){cout<<"NO ANSWER!";return 0;}q.push(a);                          //将字符串A压入队列bb.push(0);                         //将初始步数0压入队列k=bfs();                            //宽搜if (k==-1)                          //返回-1说明NO ANSWER!{cout<<"NO ANSWER!";return 0;}cout<<k;                            //输出最小步数
}

状压搜索

就是在搜索过程中应用了状态压缩思想
状态压缩：原状态不容易表达或者状态太多，内存不够用，所以用一个数的二进制表示状态可以节省很多内存空间（当然也有使用的局限性）
例子：
一排10个座位，编号从左到右分别是1到10
其中第2,4，6,8的位置上没人，我们如何记录这个状态？
有人的是1，没人的是0
1101110101（二进制）

& ---- 按位与，可以将某个数的某二进制位置为0，也可以用于取出某个二进制位
| ---- 按位或，可以将某个数的某二进制位置为1.
~ ---- 非，将一个数的所有二进制位取反
^ ---- 异或，相同为0，不同为1

常为BFS与状态压缩结合（因为用DFS不好保存状态，写起来麻烦些）

例题：

hdu 5094 Maze