题目描述

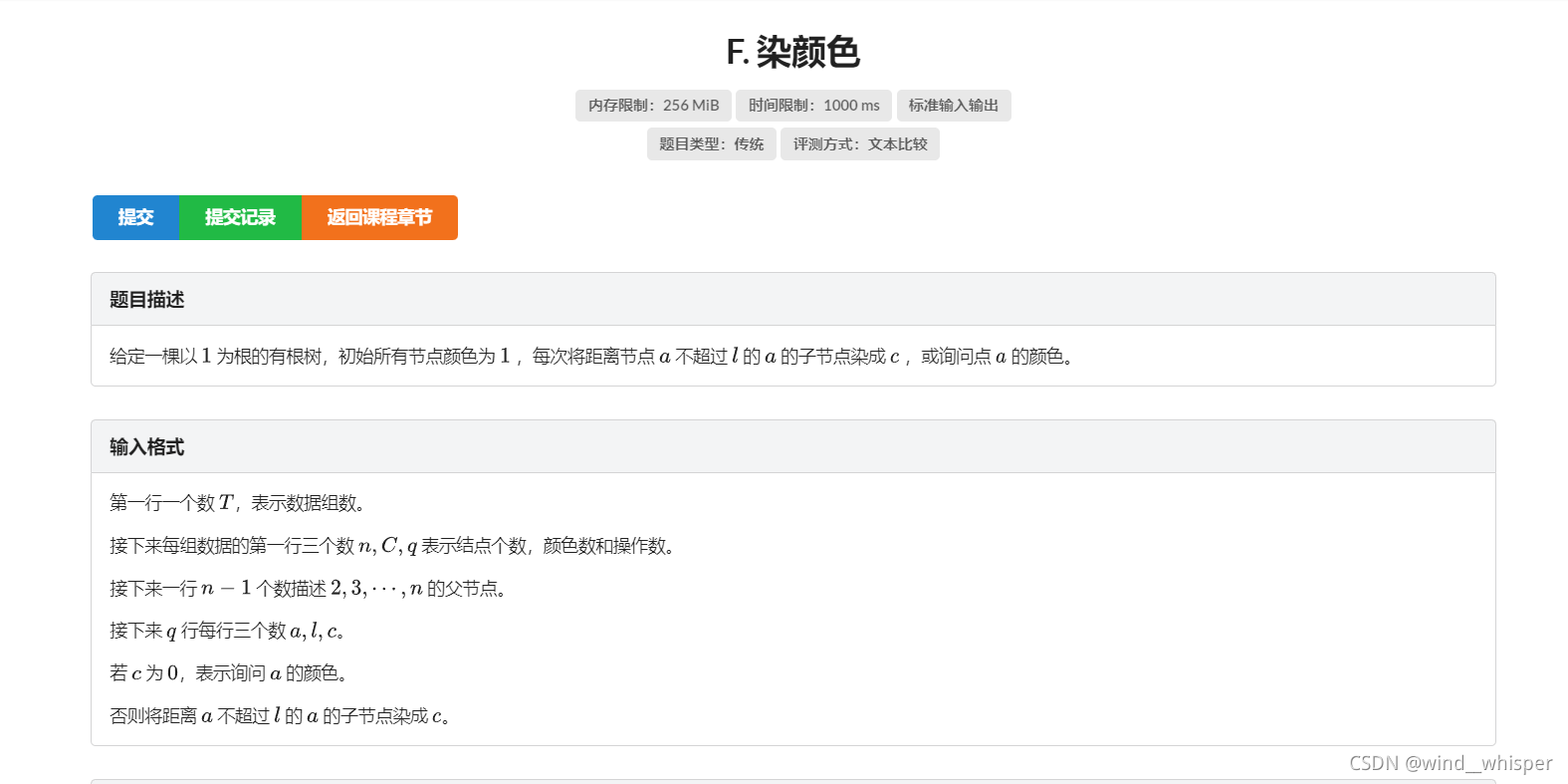
数据范围

$n\le 10^5,T\le 5$

解析

关键是对问题的转化
考虑一次修改，一个点需要满足哪些条件才可以满足

1.与x的距离不超过$l$
2.在x的子树内

这两个条件可以转化为对深度的限制和对dfs序的限制
这样本题就变成一个二维平面区间修改单点查询的问题
问题得以解决

代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+100;
const int M=2e6+100;
const int mod=1e9+7;
#define ll long long
ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-')f=-1;c=getchar();};while(isdigit(c)){x=x*10+c-'0';c=getchar();};return x*f;
}
struct edge{int to,nxt;
}e[N];
int fi[N],cnt;
void addline(int x,int y){e[++cnt]=(edge){y,fi[x]};fi[x]=cnt;
}
int dfn[N],siz[N],dep[N],tim;
void dfs(int x){siz[x]=1;dfn[x]=++tim;for(int i=fi[x];~i;i=e[i].nxt){int to=e[i].to;//printf("x=%d to=%d\n",x,to);dep[to]=dep[x]+1;dfs(to);siz[x]+=siz[to];}return;
}
int n,m,tot,a[N],rub[N];
//x[0]:dep x[1]:dfs
struct point{int x[2];}p[N];
int F,top;
bool cmp(point a,point b){return a.x[F]<b.x[F];}
point now;
int dis(point a,point b){return abs(a.x[0]-b.x[0])+abs(a.x[1]-b.x[1]);}
struct node{int mn[2],mx[2];int siz,ls,rs,laz,col;point o;
}tr[N];
void pushup(int x){int l=tr[x].ls,r=tr[x].rs;tr[x].mn[0]=tr[x].mx[0]=tr[x].o.x[0];tr[x].mn[1]=tr[x].mx[1]=tr[x].o.x[1];if(l){tr[x].mn[0]=min(tr[x].mn[0],tr[l].mn[0]);tr[x].mx[0]=max(tr[x].mx[0],tr[l].mx[0]);tr[x].mn[1]=min(tr[x].mn[1],tr[l].mn[1]);tr[x].mx[1]=max(tr[x].mx[1],tr[l].mx[1]);}if(r){tr[x].mn[0]=min(tr[x].mn[0],tr[r].mn[0]);tr[x].mx[0]=max(tr[x].mx[0],tr[r].mx[0]);tr[x].mn[1]=min(tr[x].mn[1],tr[r].mn[1]);tr[x].mx[1]=max(tr[x].mx[1],tr[r].mx[1]);}tr[x].siz=tr[l].siz+tr[r].siz+1;return;
}
void print(int k){printf("k=%d (%d %d) ls=%d rs=%d mn=(%d %d),mx=(%d %d)\n",k,tr[k].o.x[0],tr[k].o.x[1],tr[k].ls,tr[k].rs,tr[k].mn[0],tr[k].mn[1],tr[k].mx[0],tr[k].mx[1]);
}
int New(point o,int v){int x=top?rub[top--]:++tot;tr[x].o=o;tr[x].col=v;tr[x].ls=tr[x].rs=0;pushup(x);tr[tot].laz=-1;return x;
}
int build(int l,int r,int f){if(l>r) return 0;int mid=(l+r)>>1;F=f;nth_element(p+l,p+mid,p+r+1,cmp);int k=New(p[mid],1);tr[k].ls=build(l,mid-1,f^1);tr[k].rs=build(mid+1,r,f^1);pushup(k);//print(k);return k;
}
bool in(int x1,int y1,int x2,int y2,int X1,int Y1,int X2,int Y2){return x1>=X1&&x2<=X2&&y1>=Y1&&y2<=Y2;
}
bool out(int x1,int y1,int x2,int y2,int X1,int Y1,int X2,int Y2){return x1>X2||x2<X1||y1>Y2||y2<Y1;
}
void pushdown(int k){int o=tr[k].laz,l=tr[k].ls,r=tr[k].rs;tr[k].laz=-1;if(o==-1) return;if(l){tr[l].laz=tr[l].col=o;}if(r){tr[r].laz=tr[r].col=o;}return;
}
bool operator == (const point a,const point b){return a.x[0]==b.x[0]&&a.x[1]==b.x[1];}
void change(int k,point a,point b,int c){//printf("change:k=%d (%d %d) (%d %d)\n",k,a.x[0],a.x[1],b.x[0],b.x[1]);if(in(tr[k].mn[0],tr[k].mn[1],tr[k].mx[0],tr[k].mx[1],a.x[0],a.x[1],b.x[0],b.x[1])){//printf("return :k=%d\n",k);tr[k].laz=tr[k].col=c;return;}if(in(tr[k].o.x[0],tr[k].o.x[1],tr[k].o.x[0],tr[k].o.x[1],a.x[0],a.x[1],b.x[0],b.x[1])) tr[k].col=c;if(out(tr[k].mn[0],tr[k].mn[1],tr[k].mx[0],tr[k].mx[1],a.x[0],a.x[1],b.x[0],b.x[1])) return;pushdown(k);int l=tr[k].ls,r=tr[k].rs;if(l) change(l,a,b,c);if(r) change(r,a,b,c);pushup(k);
}
int ask(int k,point u){if(tr[k].o==u) return tr[k].col;if(!k||(out(tr[k].mn[0],tr[k].mn[1],tr[k].mx[0],tr[k].mx[1],u.x[0],u.x[1],u.x[0],u.x[1]))) return -1;pushdown(k);int res=max(ask(tr[k].ls,u),ask(tr[k].rs,u));return res;
}
int r;
int ans=2e9;
int main(){int T=read();while(T--){memset(fi,-1,sizeof(fi));cnt=-1;n=read();int iakoshfdoiwefc=read();m=read();for(int i=2;i<=n;i++){int x=read();addline(x,i);}dfs(1);for(int i=1;i<=n;i++){p[i]=(point){dep[i],dfn[i]};//	printf("i=%d dep=%d dfn=%d\n",i,dep[i],dfn[i]);}//	printf("\n");tot=0;r=build(1,n,0);ll ans=0;for(int i=1;i<=m;i++){//printf("\n");int x=read(),l=read(),op=read();if(!op){point u=(point){dep[x],dfn[x]};ll res=ask(r,u);ans+=1ll*i*res%mod;ans%=mod;//printf("i=%d res=%lld\n",i,res);}else{point u=(point){dep[x],dfn[x]};point v=(point){dep[x]+l,dfn[x]+siz[x]-1};change(r,u,v,op);}}printf("%lld\n",ans);}return 0;
}
/**/