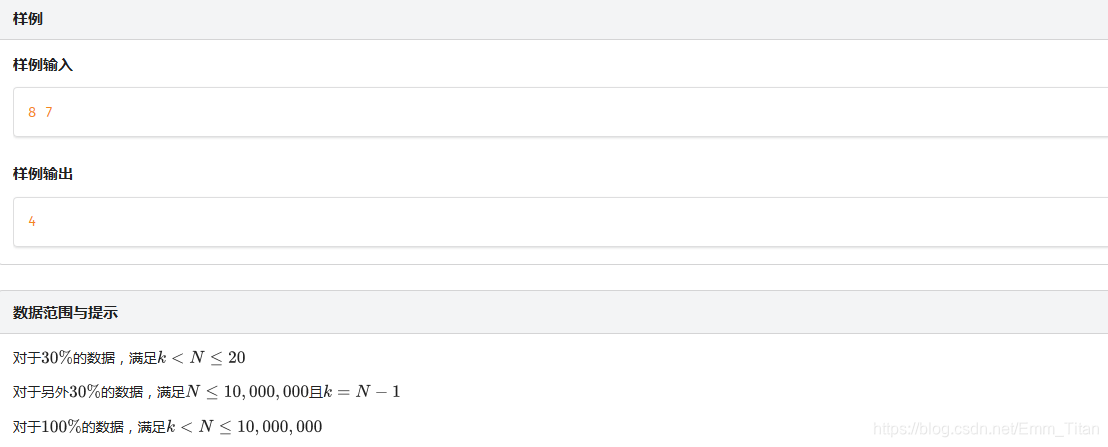
T1：小P的lol

title

solution

此题非常水…
先用素数筛，筛出$[1,n]$中的质数
质数越小，倍数的分布就越密集
所以质数一定是从小开始往大的取
然后就是暴力跑，考试的时候我以为暴力会$T$，一直在思考打容斥，幸好最后交的是暴力，嘻嘻~

code

#include <cstdio>
#define MAXN 10000005
int n, k, cnt, ans;
int prime[MAXN];
bool vis[MAXN], flag[MAXN];void init() {for( int i = 2;i <= n;i ++ ) {if( ! vis[i] ) {vis[i] = 1;prime[++ cnt] = i;}for( int j = 1;j <= cnt && i * prime[j] <= n;j ++ ) {vis[i * prime[j]] = 1;if( i % prime[j] == 0 ) break;}}
}int main() {scanf( "%d %d", &n, &k );init();if( k == n - 1 ) return ! printf( "%d", cnt );for( int i = 1;i <= cnt;i ++ ) {for( int j = prime[i];j <= n;j += prime[i] ) {if( flag[j] == 0 ) {flag[j] = 1;ans ++;if( ans >= k ) return ! printf( "%d", i );}}}return 0;
}

T2：创世纪

title

applepi手里有一本书《创世纪》，里面记录了这样一个故事……

上帝手中有着N 种被称作“世界元素”的东西，现在他要把它们中的一部分投放到一个新的空间中去以建造世界。每种世界元素都可以限制另外一种世界元素，所以说上帝希望所有被投放的世界元素都有至少一个没有被投放的世界元素能够限制它，这样上帝就可以保持对世界的控制。
由于那个著名的有关于上帝能不能制造一块连自己都不能举起的大石头的二律背反命题，我们知道上帝不是万能的，而且不但不是万能的，他甚至有事情需要找你帮忙——上帝希望知道他最多可以投放多少种世界元素，但是他只会O(2^N) 级别的算法。虽然上帝拥有无限多的时间，但是他也是个急性子。你需要帮助上帝解决这个问题。

输入格式
第一行是一个整数N，表示世界元素的数目。
第二行有 N 个整数A1, A2, …, AN。Ai 表示第i 个世界元素能够限制的世界元素的编号。

输出格式
一个整数，表示最多可以投放的世界元素的数目。

样例
样例输入
6
2 3 1 3 6 5
样例输出
3

数据范围与提示
样例说明
选择2、3、5 三个世界元素即可。分别有1、4、6 来限制它们。

数据范围与约定
对于30% 的数据，N≤10。
对于60% 的数据, N≤10^5。
对于 100% 的数据，N≤10^6，1≤Ai≤N，Ai≠i。

solution

贪心
考场上通过找规律我发现了
环的点大小为奇数，产生的贡献是$cnt>>1$
环的点大小为偶数，产生的贡献还是$cnt>>1$

通过输入的要求，可以知道最后图一定是以链+环的形式
先处理链的形式，每两个绑一起产生1的贡献，可以类似拓扑去跑
但是链与环的交接处那个点是在环的时候去产生贡献，不要在链的时候搞
最后跑出环的大小，计算贡献

code

#include <cstdio>
#define MAXN 1000005
int n, l = 1, r, ans;
int v[MAXN], d[MAXN], st[MAXN];
bool vis[MAXN];int main() {scanf( "%d", &n );for( int i = 1;i <= n;i ++ ) {scanf( "%d", &v[i] );d[v[i]] ++;}for( int i = 1;i <= n;i ++ )if( ! d[i] ) st[++ r] = i;while( l <= r ) {if( ! vis[st[l]] && ! vis[v[st[l]]] ) {ans ++;vis[v[st[l]]] ++;if( -- d[v[v[st[l]]]] == 0 )st[++ r] = v[v[st[l]]];}vis[st[l ++]] = 1;}for( int i = 1;i <= n;i ++ )if( ! vis[i] ) {int cnt = 0, j = i;while( v[j] != i )vis[j] = 1, j = v[j], cnt ++;vis[j] = 1;ans += ( cnt + 1 ) >> 1;}printf( "%d", ans );return 0;
}

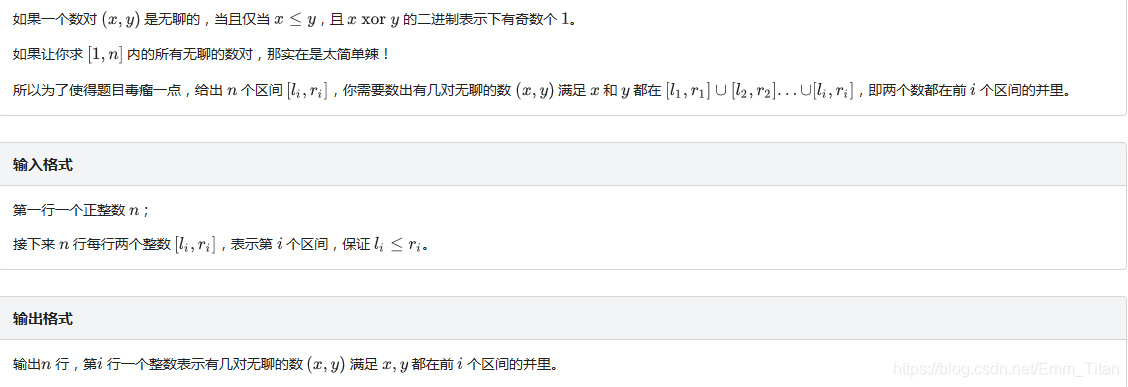
T3：无聊的数对

title

solution

要求$i\otimes j=k$中$k$的二进制中1的个数为奇数
此时$i,j$的要求是一奇一偶

证明如下：

先温习一下二进制的异或法则
$1\otimes 1=0$
$0\otimes 0=0$
$1\otimes 0=1$

①
如果$i,j$二进制的第$p$位不相等，有一个为$1$，异或后还是$1$
$1$的个数奇偶性不改变
②
如果相等
1）两个都为$0$，异或为$0$，也不会对$1$的奇偶性造成改变
2）两个都为$1$，那么异或后变成$0$，个数减掉$2$，奇偶性没改变
综上，$i,j$中$1$的奇偶性是永远不会改变的
奇数+奇数=偶数，偶数+偶数=偶数，奇数+偶数=奇数
所以必须要一奇一偶，证明完毕！

再观$l,r$十分庞大，已经超出$int$边界
但是不要怕，静态区间求个数之类的题，最喜欢丢线段树上面了
我们就维护一棵线段树，把区间操作丢上去
然后分别统计二进制$1$为奇数的个数和二进制$1$为偶数的个数
进行乘法操作，直接用根的信息即可
注意： 被完全覆盖的区间记得打懒标记，因为这个区间被完全包含了，是不会产生新贡献的

这道题其实也就这样吧…

code

#include <cstdio>
#define ll long long
#define MAXN 100005
int n, cnt, root;
ll l, r;
//odd表示区间[l,r]内二进制中1为奇数的个数
//even表示区间[l,r]内二进制中1为偶数的个数 
ll find( ll x ) {if( x & 1 ) return ( x + 1 ) >> 1;return ( x >> 1 ) + __builtin_parityll( x );
}bool flag[MAXN];
int lson[MAXN << 2], rson[MAXN << 2];
ll odd[MAXN], even[MAXN];void modify( int &t, ll l, ll r, ll L, ll R ) {if( flag[t] ) return;if( ! t ) t = ++ cnt;if( L <= l && r <= R ) {flag[t] = 1;odd[t] = find( r ) - find( l - 1 );even[t] = r - l + 1 - odd[t];return;}ll mid = ( l + r ) >> 1ll;if( L <= mid ) modify( lson[t], l, mid, L, R );if( mid < R ) modify( rson[t], mid + 1, r, L, R );odd[t] = odd[lson[t]] + odd[rson[t]];even[t] = even[lson[t]] + even[rson[t]];
}int main() {scanf( "%d", &n );for( int i = 1;i <= n;i ++ ) {ll l, r;scanf( "%lld %lld", &l, &r );modify( root, 1, ( 1ll << 32 ) - 1, l, r );printf( "%lld\n", odd[1] * even[1] );}return 0;
}

终于时隔多年，我补完了完整的一场狂欢赛！！！