参考文章

01分数规划

什么是01分数规划：
给定n个a[i]和b[i]，a[i]和b[i]绑定在一起要选同时选，求sum(a[i]) 除以 sum(b[i]) 的最大值，sum为求和函数
对于这种问题我们可以多定义一个数组x[1…n]，x为bool型只取0或者1,表示不选或者选，则对于每个x[1…n]的答案为：

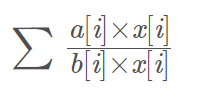
那么这类问题称之为01分数规划问题

解决方法：

题目要求选几个，只需要根据d[i]的大小来选就可以了
ans则可以通过二分x来求，判断条件
f(x) =

如果max(f(x))>0,则x < ans
如果max(f(x))<0,则x > ans
二分一个x时，每个d[i]都可以求出，现在的目标就是找到一组{xi}使得d[i] * xi最大（即求max{f( r )}）。
如何找到这一组{xi},可以直接求得max{f( r )},也可以借助最短路算法判断是否存在负环

问题模型2 最优比率生成树

一个带权无向图G，n个节点，对于图中每条边ei，都有valuei和costi，现在求一颗生成树T，最大（小）化 ∑value[i]/ ∑ cost[i],ei ∈ T

解决方法：

01分数规划模型，如果ei∈T则xi = 1 否则 xi =0
二分答案r
如何验证答案r？
边赋权ans[i] = value[i] - r * cost[i]
因为是生成树，边的数量确定，那么max{f( r )}需要取前n-1大的ans[i],也就是求最大生成树，按最大生成树权值的正负性来二分，最小化就是求最小生成树

最优比率环

给定有点权和边权的图，求一个环，使得环的点权和与边权和的比值最大

解决方法：

还是套用01分数规划模型，点权为value[i],边权为cost[u],一个环为C，问题要求最大化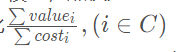

最小化就是符号倒过来
和之前一样处理，设当前答案为r，设边权为dis[i] = r * ∑cost[i] - ∑value[i]
如果r < r *,则说明至少存在一个环，d[i] < 0,也就是存在负权回环，边权值并不是提前算好，而是在更新路径的时候从哪个点访问到这个边的就将这条边设为相应点权与边权的对应值
如果r > r * ,则不存在负环
判负环一半用spfa，方法：一个点不能入队n次，否则有负环；一条最短路径长度不能到n，否则有负环。貌似后者更快

例题：

[POJ2976]Dropping tests
[POJ2728]Desert King
[POJ3621]Sightseeing Cows