title

戳一戳

solution

直接设$dp[i][k]$表示以$i$为根时，子树内，边权为$k$时的答案
（定义写得好复杂，可略过）
考虑对于点$u$，$v$是他的一个儿子，两点之间的权值为$k$
①$k=0$，那么$v$的子树内可以走$1/0$的边权
$$dp[u][0]+=dp[v][1]+dp[v][0]+1$$
②$k=1$，那么在$v$子树内就必须要一直走边权为$1$的边
$$dp[u][1]+=dp[v][1]+1$$
转移方程式中的$1$表示统计点对$(u,v)$
这就是第一个$dfs$应该做的事，默认以$1$为根进行一次树$dp$

---

接下来思考第二个$dfs$换根
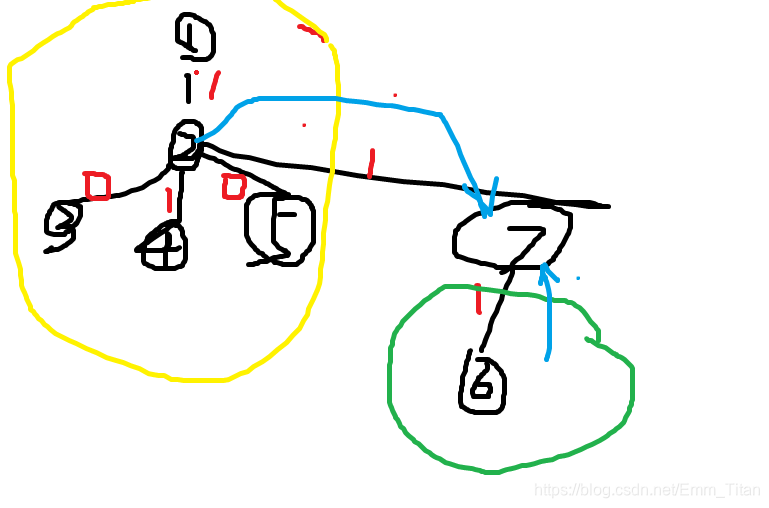考虑由根$u:2$转移到根为$v:7$的答案
首先$7$的子树也就是绿圈圈内的答案是不会有改变的，继续储存在$dp[v][k],k\in [0,1]$中
但是$7$的父亲$2$在换根时就会变成他的儿子，也会对其造成贡献也就是黄色圈圈，但是必须要把以前$7$产生的贡献剔除
所以此时也应该分类讨论$2-7$边权，设$u$对$v$产生的贡献为$w$
①$k=0$
$$w=dp[u][0]+dp[u][1]-dp[v][0]-dp[v][1]-1$$
②$k=1$
$$w=dp[u][1]-dp[v][1]-1$$
综上：
$$dp[v][k]+=w+1$$

code

#include <cstdio>
#include <vector>
using namespace std;
#define ll long long
#define N 200005
vector < pair < int, int > > G[N];
int n;
ll f[N][2];void dfs1( int u, int fa ) {for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i].first, w = G[u][i].second;if( v == fa ) continue;dfs1( v, u );if( w == 1 )f[u][w] += f[v][w] + 1;elsef[u][w] += f[v][w] + f[v][!w] + 1;}
}void dfs2( int u, int fa ) {for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i].first, w = G[u][i].second;if( v == fa ) continue;if( w ) f[v][w] += f[u][w] - f[v][w];else f[v][w] += f[u][w] + f[u][!w] - f[v][!w] - f[v][w];dfs2( v, u );}
}int main() {scanf( "%d", &n );for( int i = 1, u, v, w;i < n;i ++ ) {scanf( "%d %d %d", &u, &v, &w );G[u].push_back( make_pair( v, w ) );G[v].push_back( make_pair( u, w ) );}dfs1( 1, 0 );dfs2( 1, 0 );ll ans = 0;for( int i = 1;i <= n;i ++ )ans += f[i][0] + f[i][1];printf( "%lld", ans );return 0;
}

明明这么简单，我竟然做了这么久！！！凸(艹皿艹 )！！！