点击蓝字

关注我

微软的Azure DevOps是一款软件开发管理工具，整合了需求、代码、编译、测试、发布等所有功能于一身。今天我们就来看看如何用Azure DevOps对自己GitHub上的项目做持续集成，并能在GitHub显示最新编译状态。

其实在不久之前，Azure DevOps 曾经叫做Visual Studio Team Service，本地版叫做 Team Foundation Server (TFS)，为了体现拥抱开源，包容一切的全新微软形象，改名部有一次立功了，去掉了容易让人误解为微软Only的 "Visual Studio" Brand，并且更加侧重于云端。

新建Azure DevOps项目

让我们进入正题，首先，你需要在Azure DevOps上新建一个Project，这个Project仅仅用于编译代码，你可以完全无视代码托管、测试、发布等其他功能。建立完成之后，点这个蓝色的小火箭，旧可以经入Pipeline功能。

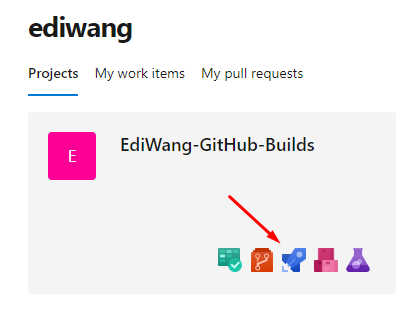
新建编译管线

在Pipeline里选择Build，然后在New菜单里选择New build pipeline

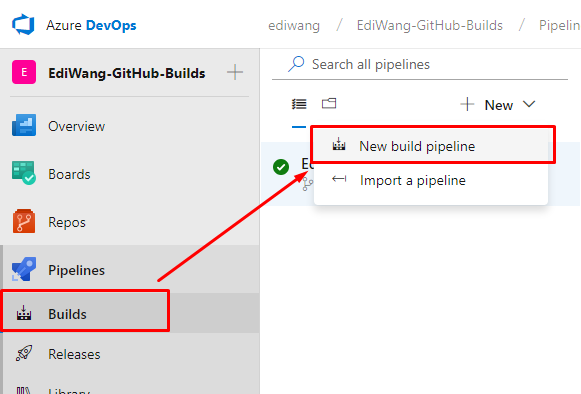
连接GitHub项目

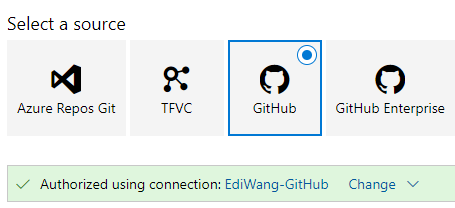
然后选择GitHub。注意：如果你之前没有在Azure DevOps里连接过GitHub，那么这一步里你需要进行授权认证，允许Azure DevOps访问你的GitHub资源。

连接完成后，选择你的Repository以及branch

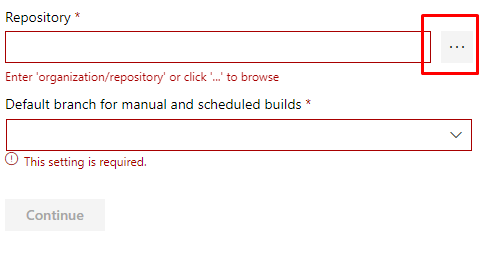
比如我需要编译 Edi.ImageWatermark 这个项目

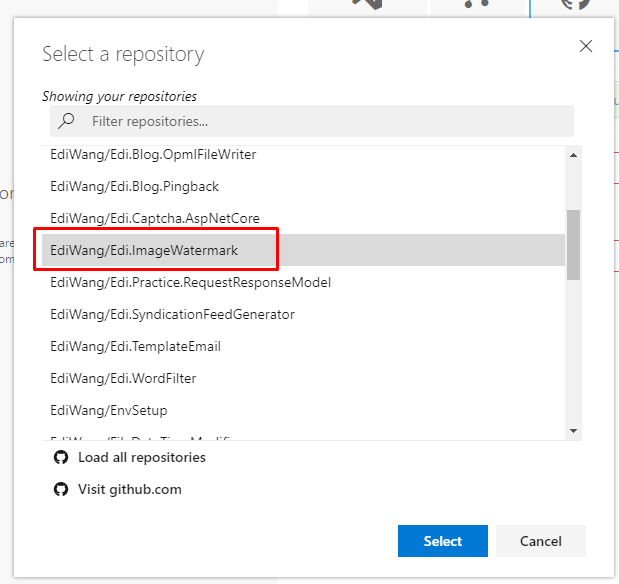
然后点击"Continue"，进入编译配置页面

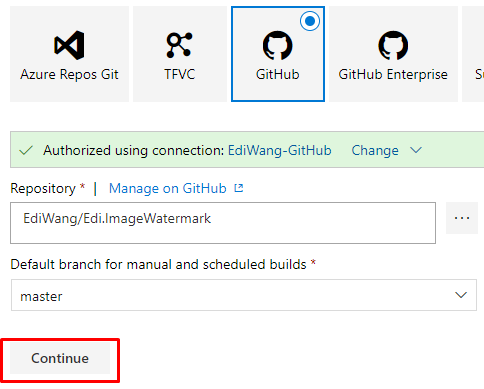
配置编译步骤

我的这个工程是一个.NET Standard 2.0的类库，因此我选择.NET Desktop模板。这里可以根据你的项目类型，选择预定义的模板，比如安卓、iOS、各种语言的网站项目等等。实在没有的话，也可以新建空模板自己配置每一个步骤。

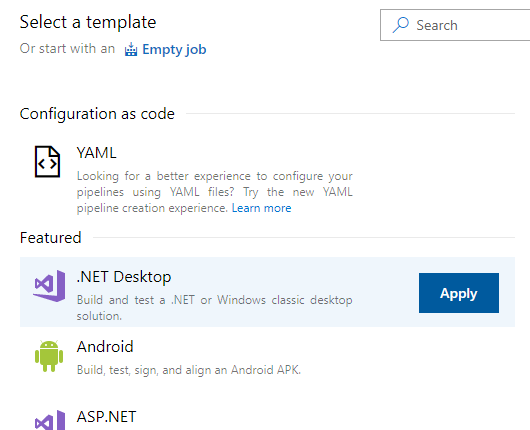
然后记得改编译管线的标题，让自己易于记住和管理

根据自己的需要，修改每一个编译步骤，比如我喜欢用最新版的NuGet，我旧可以把版本号改成4.9.2

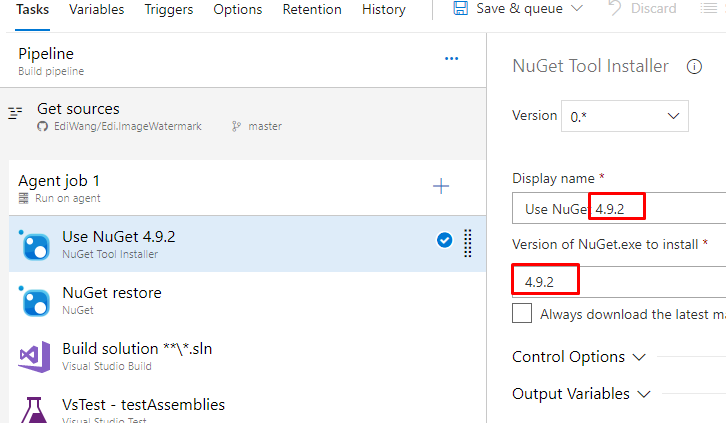
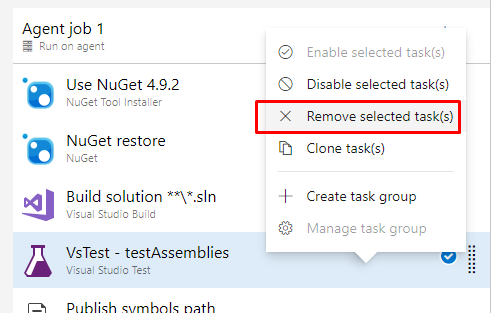
并且我不需要测试，因为我的工程里并没有单元测试项目，因此我可以删除Test的步骤。

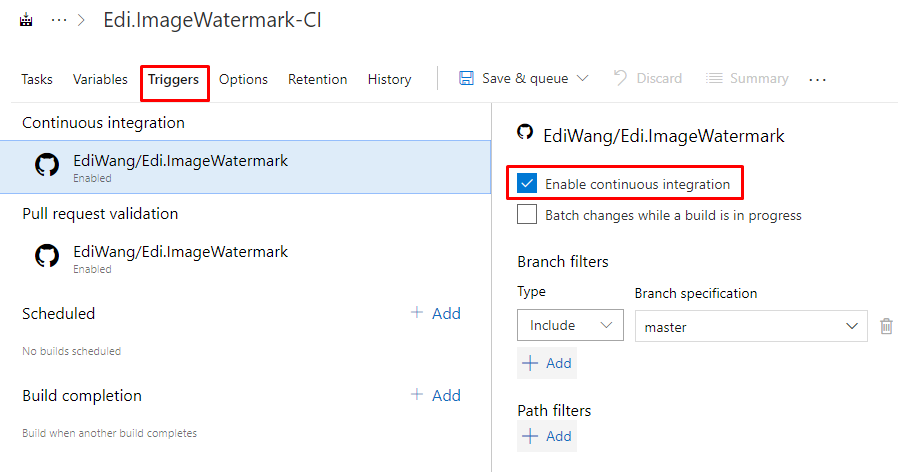
启用持续集成

想要每一次GitHub收到commit都进行编译的话，在Trigger里选择Enable continuous integration

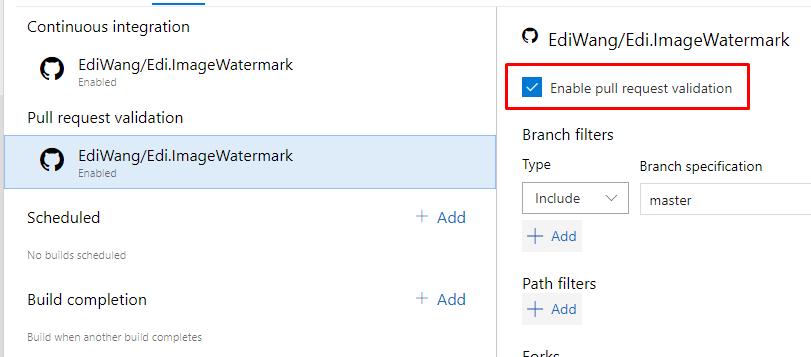
类似的，如果当有人给你提PR的时候想要进行编译，也可以勾选 Enable pull request validation

使用编译状态图标

在Options选项卡里复制Markdown link

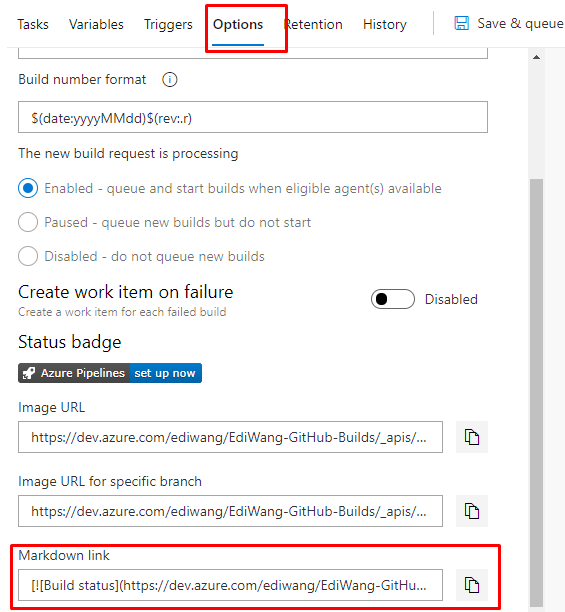
然后粘贴到你GitHub工程的Readme.md里去，并且提交commit

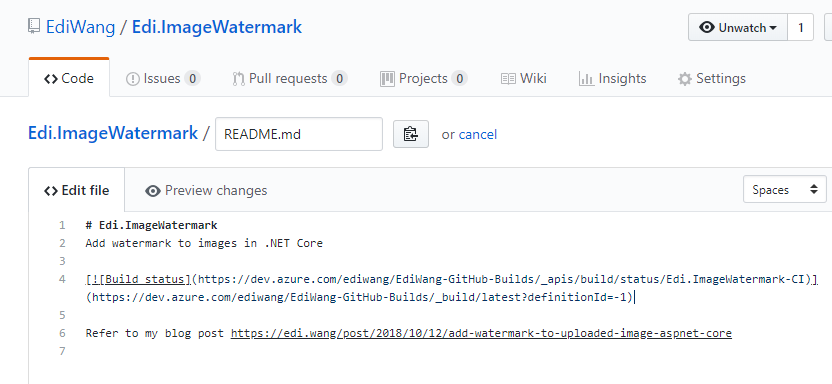
这样你就得到了一个最新编译状态的图标

保存并测试编译管线

回到Azure DevOps，点击"Save & queue"

可以看到一个Build已经启动了

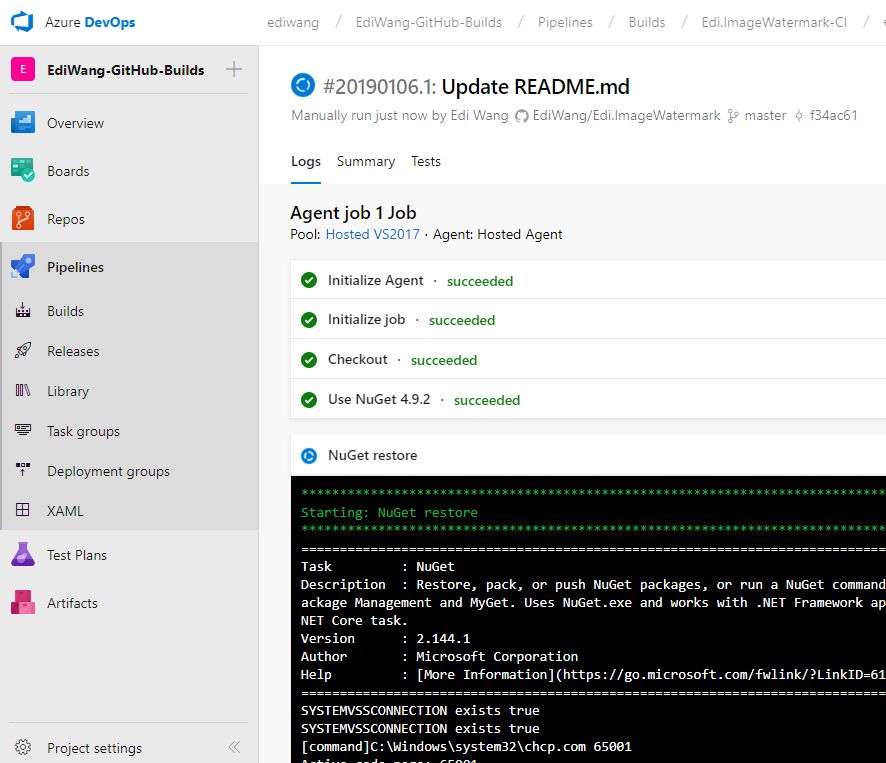
点进去还可以看到详细的编译过程

如果一切顺利，编译成功后，你的GitHub项目主页就会出现绿色succeeded的字样。并且以后一旦这个工程有新的commit提交到GitHub，都会触发持续集成的编译，并更新这个状态图标。