题目描述

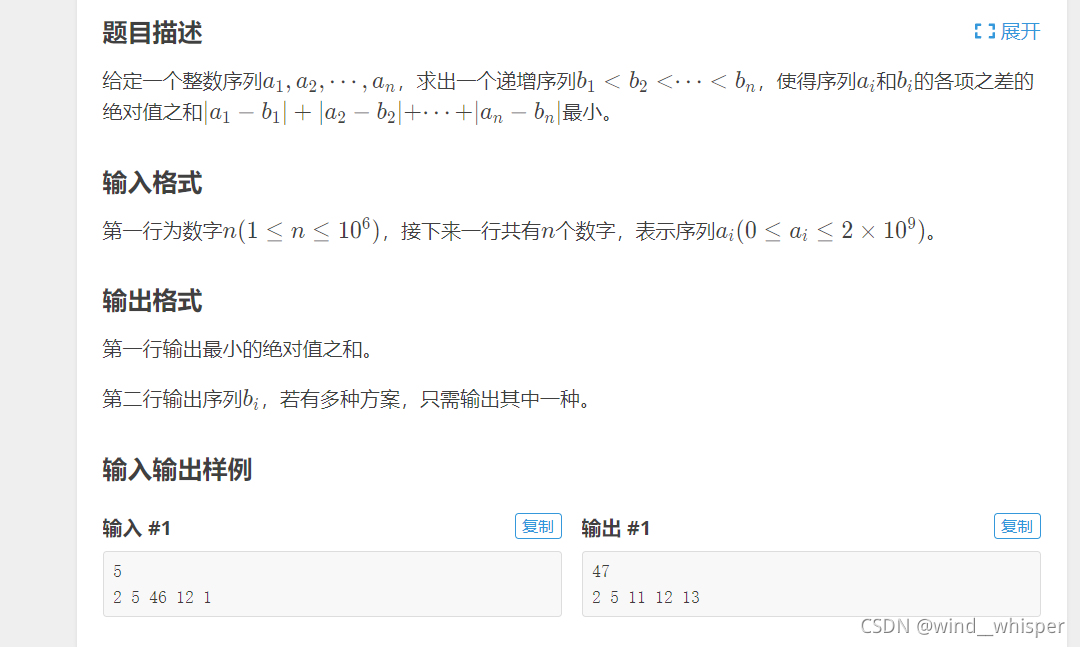
数据范围

$n<=1e6$

解析

先考虑简单情况
如果原数列是单调递增的，显然应该使$b_i=a_i$
如果单调递减，应该取中位数
那么原数列如果分成单调递减的几段，那么每一段都取中位数使最好的
但是这样会有非法的情况，因为中位数不一定单调递增
所以我们把中位数递减的区间合并，再求大区间的中位数即可
那么怎么快速维护合并区间中位数呢？
主席树最棒了
考虑对每个区间建一个堆，pop掉一半的元素，这样堆顶就是中位数了
再把两个区间的堆合并即可
考虑正确性，为什么不会提前pop掉未来的中位数？
因为如果需要合并，左边中位数大于右边，那么未来的中位数一定是不比左边的中位数大的
而关键就是右边的堆先合并再pop
《巧夺天工》
（说实话我觉得本题主席树真的挺可做的）

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e6+100;
const int M=1050;
const int mod=998244353;
ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}while(isdigit(c)){x=x*10+c-'0';c=getchar();}return x*f;
}
int n,m,tot,num;
int val[N],ls[N],rs[N],rot[N],dis[N],a[N],siz[N];
int New(int v){++tot;val[tot]=v;return tot;
}
int merge(int x,int y){if(!x||!y) return x|y;if(val[x]<val[y]) swap(x,y);rs[x]=merge(rs[x],y);if(dis[ls[x]]<dis[rs[x]]) swap(ls[x],rs[x]);dis[x]=dis[rs[x]]+1;return x;
}
void del(int &x){//printf("    del:id=%d %d\n",x,val[x]);x=merge(ls[x],rs[x]);//printf("nx=%d\n",x);
}
int st[N],ed[N],l[N],r[N];
inline void cut(int x){l[r[x]]=l[x];r[l[x]]=r[x];
}
int b[N];
struct node{int l,r,val,rt,siz;
}s[N];
int top;
int main(){
//	freopen("a.in","r",stdin);
//	freopen("a.out","w",stdout);n=read();dis[0]=-1;for(int i=1;i<=n;i++){a[i]=read();a[i]-=i;}	for(int i=1;i<=n;i++){s[++top]=(node){i,i,a[i],New(a[i]),1};while(top>1&&s[top-1].val>s[top].val){top--;s[top].siz+=s[top+1].siz;s[top].rt=merge(s[top].rt,s[top+1].rt);s[top].r=s[top+1].r;while(s[top].siz>(s[top].r-s[top].l+2)/2){del(s[top].rt);s[top].siz--;}s[top].val=val[s[top].rt];}}for(int i=1;i<=top;i++){for(int j=s[i].l;j<=s[i].r;j++){b[j]=s[i].val;}}ll tot=0;for(int i=1;i<=n;i++){tot+=abs(a[i]-b[i]);}printf("%lld",tot);return 0;
}
/**/