概念：

概率
期望：数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

例题

引入：

甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，赢家可以获得
100法郎的奖励。当比赛进行到第四局的时候，甲胜了两局，乙胜了一局，这时由于某些原
因中止了比赛，那么如何分配这100法郎才比较公平？

解答：

乙获胜概率是1/4，甲是3/4，所以按照这个分钱

Happy Running NC15532

题意：

小明需要在操场顺时针跑圈打卡，操场上有两个打卡点A，B， 他需要先在A点打卡，然后在B点打卡（哪怕B点在A点前面），打完卡就可以结束跑步了，他的起点以及A，B两点的位置是随机的，告诉你操场的长度X米，求他需要跑超过K米的概率。
先输入K，再输入X
输入：

3 
2 2
4 3
2 1

• 输出：

0.50
0.22
0.00

题解：

固定起点，分类讨论
情况1：
当A在B前：此时所跑距离小于等于一圈
列出相关式子：
K < X
A < B
B > = K
A < = x
B < = x
概率为图中阴影部分占整个正方形
即

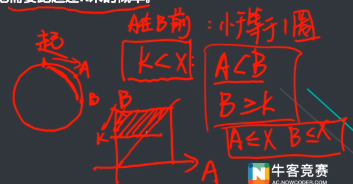
情况2：
A在B后：

情况3：
K == X时，(其实是求B在A前的概率)也就是0.5

代码：

poj2096 NC106693 Collecting Bugs

题意：

题意：
一个软件有s个子系统，会产生n种bug。
某人一天发现一个bug，这个bug属于某种bug，发生在某个子系统中。
求找到所有的n种bug，且每个子系统都找到bug，这样所要的天数的期望。
需要注意的是：bug的数量是无穷大的，所以发现一个bug，出现在某个子系统的概率是1/s，
属于某种类型的概率是1/n。
• (0 < n, s <= 1 000)
• 输入：
• 1 2
• 输出：
• 3.00000

题解：

• f[i][j]表示现在已经找到的bug有i种，属于j个系统，找完剩下所需bug的期望天数。
• 已知：f[n][s]=0，因为已经达到目标， 而要求的答案是f[0][0]
dp[i][j]状态可以转化成以下四种：
dp[i][j] 发现一个bug属于已经找到的i种bug和j个子系统中
dp[i+1][j] 发现一个bug属于新的一种bug，但属于已经找到的j种子系统
dp[i][j+1] 发现一个bug属于已经找到的i种bug，但属于新的子系统
dp[i+1][j+1]发现一个bug属于新的一种bug和新的一个子系统
以上四种的概率分别为：
p1 = i * j / (n * s)
p2 = (n-i) * j / (n * s)
p3 = i * (s-j) / (n * s)
p4 = (n-i)* (s-j) / (n * s)
又因为E(aA+bB+…) = aE(A) + bE(B)
所以dp[i,j] = p1 * dp[i,j] + p2 * dp[i+1,j] + p3 * dp[i,j+1] + p4 * dp[i+1,j+1] + 1;
dp[i,j] = ( 1 + p2 * dp[i+1,j] + p3* dp[i,j+1] + p4 * dp[i+1,j+1] )/( 1-p1 )
= ( n * s + (n-i) * j * dp[i+1,j] + i*(s-j) * dp[i,j+1] + (n-i) * (s-j) * dp[i+1 , j+1] )/( n * s - i * j )

代码：

#include<iostream>
#include<cstdio>
#include<cstring>using namespace std;const int N=1010;double dp[N][N];int main(){//freopen("input.txt","r",stdin);int n,s;while(~scanf("%d%d",&n,&s)){dp[n][s]=0;for(int i=n;i>=0;i--)for(int j=s;j>=0;j--){if(i==n && j==s)continue;dp[i][j]=(i*(s-j)*dp[i][j+1]+(n-i)*j*dp[i+1][j]+(n-i)*(s-j)*dp[i+1][j+1]+n*s)/(n*s-i*j);}printf("%.4f\n",dp[0][0]);}return 0;
}

NC210477 带富翁

题意：

• 小明在玩一款带富翁游戏，这个游戏具体来说就是有n个奖励点，每个奖励点有一定的奖励分。
一开始他站在位置1。每次他都会扔一个有6面的筛子，如果扔到了x，并且小明现在站在i这个位置，小明就会向前进x步到达i+x这个位置。
• 如果小明扔出了x并且i+x已经大于了n，那么小明就会重新扔，直到i+x在合适的位置。小明
最后如果到达了n号位置，那么小明就会结束游戏，现在小明想知道自己期望的得分是多少。

题解：

• f[i]表示从i走到n获得的金子的期望，
• i+6 <= n 即不会走出去：f[i] = a[i] + ∑(1/6 * f[j]) ( i+1<=j<=i+6)
• i+6>n f[i] = (f[i + 1] + … + f[n]) / (n - i)。

代码：

NC210481 筛子游戏

题意：

• 吉吉国王正在玩一款手游，这个手游的规则非常简单。一开始你会得到三个筛子，三个筛子分别有k1,k2,k3面，也就是说分别可以扔出[1,k1],[1,k2],[1,k3]之间数。
• 一开始的分数为0，每次扔筛子都会扔出x,y,z三个数，但是这个游戏的特别之处在于每次开
局都会给定三个数a,b,c，如果满足x=a,y=b,z=c，那么你的分数就会清零，否则你的分数就会加上x+y+z。现在吉吉国王想知道需要扔多少次才能使得他的分数大于n。 • 0≤n≤500

题解：

• 设f[i]表示达到i分时到达目标状态的期望，pk为投掷k分的概率，p0为回到0的概率，这个先预处理出来
• 则f[i]=∑(pk * f[i+k])+f[0 ] * p0+1
• f[i]=∑(pk * f[i+k])+f[0] * p0+1
• 每个状态都和f[0]有关系，而且f[0]就是我们所求，为一个常数
• 设f[i]=A[i] * f[0]+B[i];
• 代入上述方程右边得到：
• f[i]=∑(pk * A[i+k] * f[0]+pk * B[i+k])+f[0] * p0+1=
• (∑(pk* A[i+k])+p0)f[0]+∑(pk * B[i+k])+1;
• 所以 A[i]=(∑(pk* A[i+k])+p0) B[i]=∑(pk * B[i+k])+1
• 先递推求得A[0]和B[0] 那么 f[0]=B[0]/(1-A[0]);

代码：

NC210487 食堂

题意：

• 1≤k≤m≤n≤2000

题解：

• 设f[i][j]表示i个人排队,Tomato排在第j个位置，达到目标状态的概率(j<=i)
• f[n][m]就是所求
• j==1: f[i][1]=p1 * f[i][1]+p2 * f[i][i]+p4;
• 2<=j<=k: f[i][j]=p1 * f[i][j]+p2 * f[i][j-1]+p3 * f[i-1][j-1]+p4;
• k<j<=i: f[i][j]=p1 * f[i][j]+p2 * f [i][j-1]+p3 * f [i-1][j-1];

代码：

习题

CF148D Bag of mice

CF16E Fish

CF235B Let’s Play Osu!

NC14378 珂学送分

NC20263 [SCOI2008] 奖励关

NC20709 Balls

NC210515 迷宫游戏

NC210516 抽卡