快速简单记录老师口胡（可能就我自己看得懂了吧…）

T1：舞踏会

title

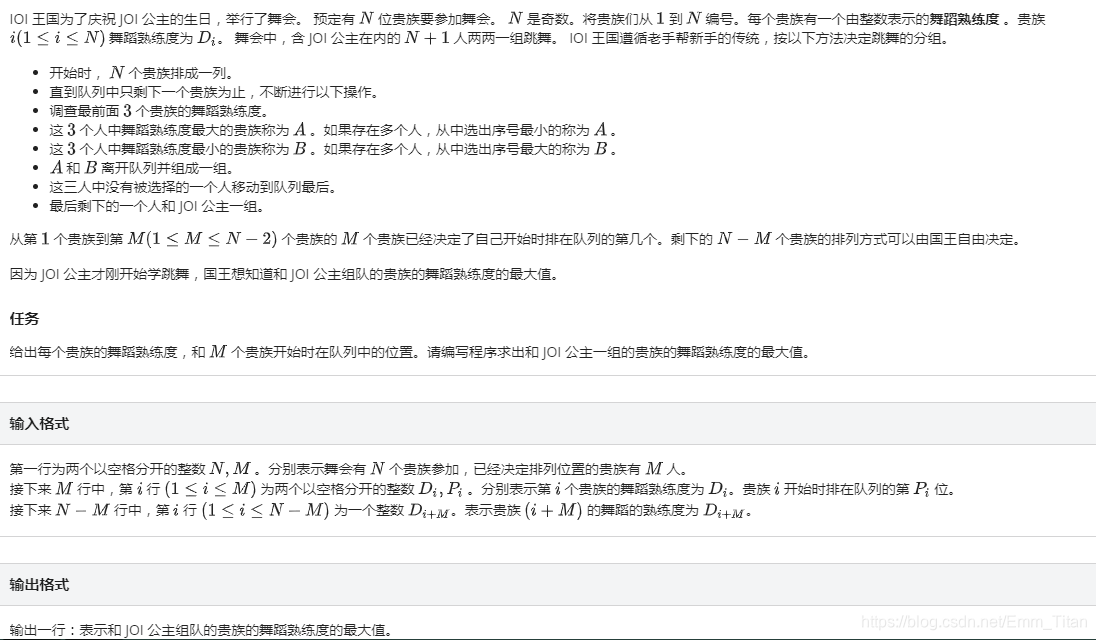
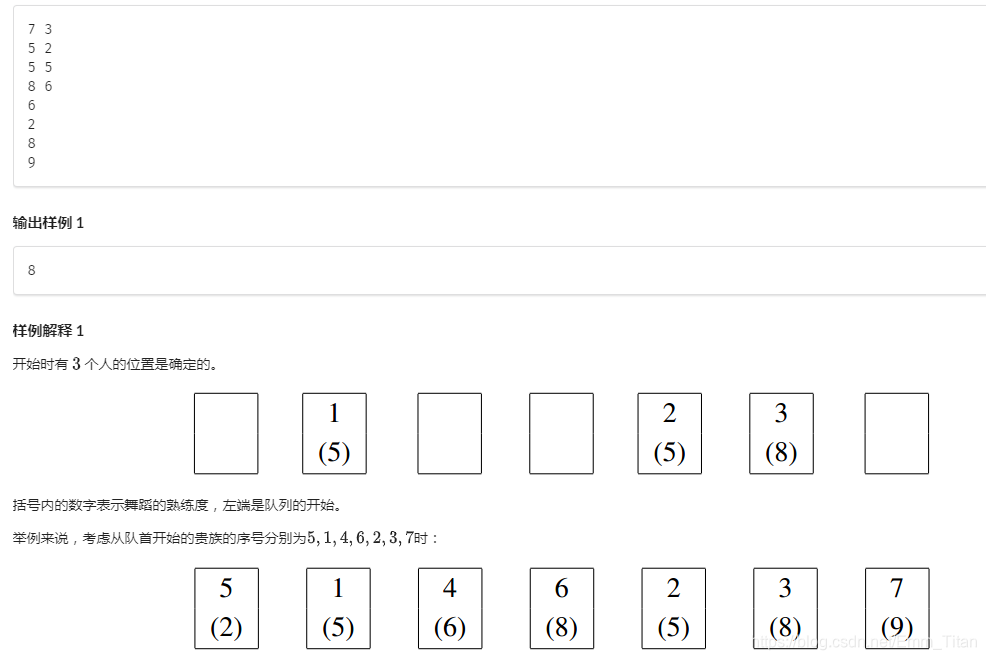
solution

对于三个人中间取中值的操作，我们可以把它弄到树上去，搞成一个三叉树
然后可以任意乱排不固定人的位置的话，也就意味着这个三叉树的形态是多变的

接着我们来定义一下这个树上的规则，对于点$fa$ 而言，他的三个儿子的权值要满足：左儿子<=中儿子<=右儿子，即$ls\le ms\le rs$
但是左儿子的右儿子就不一定也要小于$fa$的值，这个大小关系是不会传递祖宗八代都保持的哦！
这样对于该点的答案权值，直接取中间儿子的值就可以了

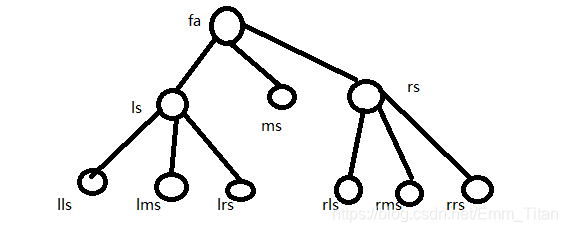
可知从$fa$ 开始一直往右走或者往下走，这一路上的值都应该大于等于$fa$，也就是说这条路经过了多少个点就必须要满足多少个点的值$>=fa$，这个$fa$的值才可能成为答案
我们定义这些点为坑，需要填充
（如果本身就有值固定了，就需要看是否$>=fa$）
而从$fa$ 开始一直往左走或者往下走，这一路上的值都应该小于等于$fa$

为了让答案更大，我们就想要坑的个数越小越好，同时要保证左子树也满足要求

code

/*
序列的1~3位以第n+1位为父节点
表示1~3位的中值会移动到第n+1位
序列的4~6位以第n+2位为父节点
以此类推......
可知点i的三个儿子分别为(i-n)*3-2, (i-n)*3-1,(i-n)*3
我们称必须大于等于答案并且没人的叶子节点为坑
显然根到每个坑的路径上没有向左的边
*/
#include <cstdio>
#include <iostream> 
#include <algorithm>
using namespace std;
#define MAXN 100005
#define INF 0x3f3f3f3f
//不能定义成0x7f7f7f7f因为后面min比较会涉及加法
//两个int上界相加则会爆出int成为负的
struct node {int val, num, rk;
}nobel[MAXN];
int n, m, N;
int p[MAXN], v[MAXN], dp[MAXN << 1];
/*
val能力值 num编号 rk排名
p[i]编号为i的位置(没有就为0)
v[i]位置为i的排名
dp[i]以i为根的子树 最少坑的数量 
n人数 N树上节点总数 也是整棵树的根 
*/
bool cmpVal ( node x, node y ) {return ( x.val == y.val ) ? x.num < y.num : x.val < y.val;
}bool cmpNum ( node x, node y ) {return x.num < y.num;
}void dfs ( int u, int ans ) {if ( u <= n ) {//u为叶子节点 if ( ! v[u] )//位置上没人需要填一个坑dp[u] = 1;else if ( v[u] >= ans )//位置上有一个满足条件的人则不需要填坑dp[u] = 0;else//不满足条件->u不能成为右子树或者中子树(非法)dp[u] = INF;//dp关于ans呈单调递增//ans越大->对v[u]的要求越高->dp[u]=0的难度就越高 }else {int t = u - n;for ( int i = t * 3 - 2;i <= t * 3;i ++ )dfs ( i, ans );dp[u] = INF;dp[u] = min ( dp[t * 3 - 2] + dp[t * 3 - 1], dp[u] );dp[u] = min ( dp[t * 3 - 2] + dp[t * 3], dp[u] );dp[u] = min ( dp[t * 3 - 1] + dp[t * 3], dp[u] );//dp关于ans呈单调递增 }
}int main() {scanf ( "%d %d", &n, &m );N = n + ( n >> 1 );//共有n/2个非叶节点//一共要淘汰n-1个人 每三个人当中淘汰两个//一个非叶节点代表三进一//所以淘汰次数为(n-1)/2 非叶节点个数也应为(n-1)/2//n又保证是奇数所以(n-1)/2=n/2 for ( int i = 1;i <= n;i ++ ) {scanf ( "%d", &nobel[i].val );nobel[i].num = i;if ( i <= m ) scanf ( "%d", &p[i] );}sort ( nobel + 1, nobel + n + 1, cmpVal );for ( int i = 1;i <= n;i ++ )nobel[i].rk = i;//按照能力排序后的排名sort ( nobel + 1, nobel + n + 1, cmpNum );for ( int i = 1;i <= m;i ++ )v[p[i]] = nobel[i].rk;int l = 1, r = n;while ( l != r ) {int mid = ( l + r + 1 ) >> 1;dfs ( N, mid );int tot = 0;//能力值>=mid的人数 用来填坑的数量//tot关于mid呈单调递减 //mid越大->rk>=mid难度越高->tot++越难触发for ( int i = m + 1;i <= n;i ++ )if ( nobel[i].rk >= mid ) tot ++;if ( dp[N] <= tot )//坑的数量比填坑的数量小则可以实现l = mid;elser = mid - 1; }sort ( nobel + 1, nobel + n + 1, cmpVal );printf ( "%d\n", nobel[l].val );return 0;
}

T2：HH去散步

title

HH有个一成不变的习惯，喜欢饭后百步走。所谓百步走，就是散步，就是在一定的时间 内，走过一定的距离。 但是同时HH又是个喜欢变化的人，所以他不会立刻沿着刚刚走来的路走回。 又因为HH是个喜欢变化的人，所以他每天走过的路径都不完全一样，他想知道他究竟有多 少种散步的方法。 现在给你学校的地图（假设每条路的长度都是一样的都是1），问长度为t，从给定地 点A走到给定地点B共有多少条符合条件的路径

输入格式
第一行：五个整数N，M，t，A，B。其中N表示学校里的路口的个数，M表示学校里的 路的条数，t表示HH想要散步的距离，A表示散步的出发点，而B则表示散步的终点。 接下来M行，每行一组Ai，Bi，表示从路口Ai到路口Bi有一条路。数据保证Ai != Bi，但不保证任意两个路口之间至多只有一条路相连接。 路口编号从0到N − 1。 同一行内所有数据均由一个空格隔开，行首行尾没有多余空格。没有多余空行。 答案模45989。

输出格式
一行，表示答案。

样例
Sample Input
4 5 3 0 0
0 1
0 2
0 3
2 1
3 2
Sample Output
4

数据范围与提示
对于30%的数据，N ≤ 4，M ≤ 10，t ≤ 10。 对于100%的数据，N ≤ 20，M ≤ 60，t ≤ 2^30，0 ≤ A,B < N。

solution

看到$n,m$跟$t$完全不在一个量级的时候，一般都会想矩阵加速等玩意儿
假设原矩阵$A[1][i]$表示从起点走到$i$点的方案数，加速矩阵$B[i][j]$表示$i->j$存在一条有向边可以这么走
注意无向边拆开的两条边不要连在一起
由于起点$a$可以一开始任意走连出去的边，所以它没有加速矩阵的统一，我们就单独算一次，加速矩阵就少做一次即可

code

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define MAXN 150
#define mod 45989
int cnt = 1, result;struct Matrix {int c[MAXN][MAXN];Matrix () {memset ( c, 0, sizeof ( c ) );}Matrix operator * ( const Matrix &a ) const {Matrix ans;for ( int i = 1;i <= cnt;i ++ )for ( int j = 1;j <= cnt;j ++ )for ( int k = 1;k <= cnt;k ++ )ans.c[i][j] = ( ans.c[i][j] + 1ll * c[i][k] * a.c[k][j] % mod ) % mod;return ans;}
}A, B;Matrix qkpow ( Matrix a, int b ) {Matrix ans;for ( int i = 1;i <= cnt;i ++ )ans.c[i][i] = 1;while ( b ) {if ( b & 1 ) ans = ans * a;a = a * a;b >>= 1;}return ans;
}int n, m, t, a, b;
int from[MAXN], to[MAXN];void add ( int u, int v ) {from[++ cnt] = u; to[cnt] = v;from[++ cnt] = v; to[cnt] = u;
}int main() {scanf ( "%d %d %d %d %d", &n, &m, &t, &a, &b );a ++; b ++;for ( int i = 1;i <= m;i ++ ) {int u, v;scanf ( "%d %d", &u, &v );u ++; v ++;add ( u, v );}for ( int i = 1;i <= cnt;i ++ )if ( from[i] == a ) A.c[1][i] ++;for ( int i = 1;i <= cnt;i ++ )for ( int j = 1;j <= cnt;j ++ )if ( to[i] == from[j] && i != ( j ^ 1 ) && i != j )B.c[i][j] ++;B = qkpow ( B, t - 1 );A = A * B;for ( int i = 1;i <= cnt;i ++ )if ( to[i] == b ) result = ( result + A.c[1][i] ) % mod;printf ( "%d", result );return 0;
}

T3：排序

title

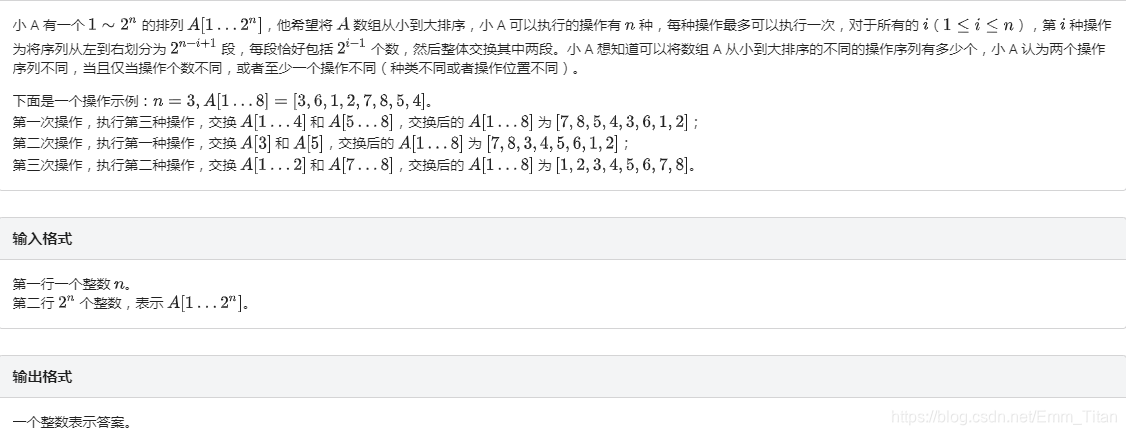
solution

有一个结论：操作顺序的调换对最后的答案没有影响
可以感性理解，自己画画反正就是举不出反例（摊手无奈┓( ´∀` )┏）
有了这个结论我们就可以知道，如果最后生成了一个不同的序列花费了$x$次操作，那么方案数就应该加上$x!$

接着题目的描述是每一次只能调换一次整体长度为$2^i$的两段序列，也可以不换
下一轮就是操作长度为$2^{i+1}$

也就是说如果本轮有超过$2$段不合法的序列，就无法完成，这个时候就可以回溯了

所以我们必须保证在$i$层的时候，答案序列分成长度$2^{i-1}$后的每一段内部都是有序的，这样在进行本轮操作后才有可能成功，举个栗子
$1234$
$i=3:3214$
可以发现必须要$2^{i-1}$整段整段调换，无论如何都无法凑出最后答案
因为他们的内部并不按从小到大有序
而如果是这个栗子就可以凑出答案
$1234$
$i=3:3412$

由此可见必须先进行长度为$1$的调换操作，然后进行长度为$2$的，以此类推才有可能保证对于$i$层而言，内部是有序的

剩下的就看代码注释吧…

code

#include <cstdio>
#include <iostream>
using namespace std;
#define int long long
#define MAXN 4100
int n, result;
int A[MAXN];void change ( int idx1, int idx2, int len ) {for ( int i = 0;i < len;i ++ )swap ( A[idx1 + i], A[idx2 + i] );
}
//注意：1234这种只是指类型，12是一种，34是一种
//比如2 3 || 9 10也符合12 34这种类型
void dfs ( int len, int x ) {if ( n == len ) {//所有类型的交换都已进行 满足的方案就有x! int ans = 1;for ( int i = 1;i <= x;i ++ )ans *= i;result += ans;return;}int L = len << 1;int tot = 0;//不合法的个数int p[3];for ( int i = 1;i <= n;i += L ) {if ( A[i] % L != 1 || A[i + len] - A[i] != len ) {tot ++;if ( tot > 2 ) return;//超过两个就无法完成 p[tot] = i;}}switch ( tot ) {case 0 : dfs ( L, x ); break;case 1 : {//21类型 需交换成为12 change ( p[1], p[1] + len, len );dfs ( L, x + 1 );change ( p[1], p[1] + len, len );break;}case 2 : {if ( A[p[1]] % L == 1 && A[p[2]] % L == 1 ) {//14 32类型 change ( p[1] + len, p[2] + len, len );dfs ( L, x + 1 );//交换成为12 34 change ( p[1] + len, p[2] + len, len );change ( p[1], p[2], len );dfs ( L, x + 1 );//交换成为34 21 change ( p[1], p[2], len );}else if ( A[p[1]] % L == 1 && A[p[1] + len] % L == 1 ) {if ( A[p[2] + len] - A[p[1] + len] == len ) {//13 24类型 （只能用4-3或者2-1判断类型！不能用3-2）//比如2 5 3 6也是符合13 24类型，这个时候5-3就≠1）//下面的判断同理change ( p[1] + len, p[2], len );dfs ( L, x + 1 );//交换成为12 34 change ( p[1] + len, p[2], len );}}else if ( A[p[2]] % L == 1 && A[p[2] + len] % L == 1 ) {//42 31类型 if ( A[p[1]] - A[p[2]] == len ) {//这个判断等价于A[p[1]+len]-A[p[2]+len]=lenchange ( p[1], p[2] + len, len );dfs ( L, x + 1 );//交换成为12 34 change ( p[1], p[2] + len, len );}}break;}} 
}signed main() {scanf ( "%lld", &n );n = 1 << n;for ( int i = 1;i <= n;i ++ )scanf ( "%lld", &A[i] );dfs ( 1, 0 );printf ( "%lld", result );return 0;
}

T4：铁路旅行

title

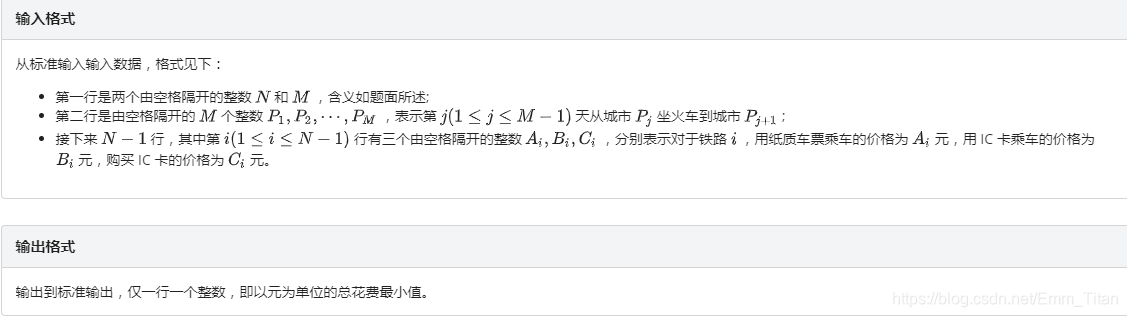
solution

首先很容易想到：
对于第i条路而言，假设第i条路走了j次，那么我们的抉择就是：
$$min(A[i]\ast j,B[i]\ast j+C[i])$$
接着发现题目的铁路是一条单链且顺次连接
意味着对于点$i,j$，铁路$i-j$都要加1
这种区间操作我们很容易就想到了线段树操作
最后再单点查询每个点走的次数即可
（实在很简单，我都不会口胡了）

code

#include <cstdio>
#include <iostream>
using namespace std;
#define MAXN 100005
#define int long long
int n, m, result;
int a[MAXN], b[MAXN], c[MAXN], p[MAXN];
int tree[MAXN << 2], flag[MAXN << 2];void pushdown ( int t, int l, int r ) {if ( ! flag[t] ) return;int mid = ( l + r ) >> 1;tree[t << 1] += flag[t] * ( mid - l + 1 );tree[t << 1 | 1] += flag[t] * ( r - mid );flag[t << 1] += flag[t];flag[t << 1 | 1] += flag[t];flag[t] = 0;
}void add ( int t, int l, int r, int L, int R ) {if ( L <= l && r <= R ) {tree[t] += ( r - l + 1 );flag[t] ++;return;}pushdown ( t, l, r );int mid = ( l + r ) >> 1;if ( L <= mid ) add ( t << 1, l, mid, L, R );if ( mid < R ) add ( t << 1 | 1, mid + 1, r, L, R );tree[t] = tree[t << 1] + tree[t << 1 | 1];
}int query ( int t, int l, int r, int id ) {if ( l == r ) return tree[t];pushdown ( t, l, r );int mid = ( l + r ) >> 1;if ( id <= mid ) return query ( t << 1, l, mid, id );else return query ( t << 1 | 1, mid + 1, r, id );
}signed main() {scanf ( "%lld %lld", &n, &m );for ( int i = 1;i <= m;i ++ )scanf ( "%lld", &p[i] );for ( int i = 1;i < m;i ++ ) {int minn = min ( p[i], p[i + 1] );int maxx = max ( p[i], p[i + 1] );add ( 1, 1, n, minn, maxx - 1 );}for ( int i = 1;i < n;i ++ )scanf ( "%lld %lld %lld", &a[i], &b[i], &c[i] );for ( int i = 1;i < n;i ++ ) {int tot = query ( 1, 1, n, i );if ( tot * ( a[i] - b[i] ) < c[i] )result += tot * a[i];elseresult += tot * b[i] + c[i];}printf ( "%lld", result );return 0;
}