LIS算是比较经典的问题，常用的是O(n^2)的方法

	for(int i=1;i<=n;i++){dp[i]=1;for(int j=1;j<i;j++){if(a[j]<a[i])dp[i]=max(dp[i],dp[j]+1);}mx=max(mx,dp[i]);}

我们这里优化成O(nlogn)
我们模拟一个栈stack，每读入一个数，如果这个数大于栈顶的数，就将它压入栈内

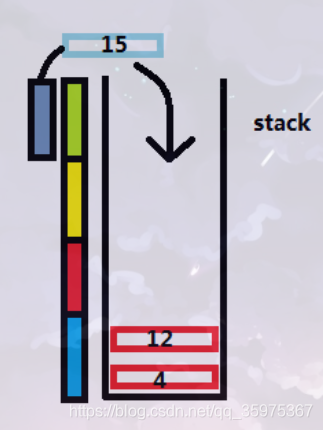
这样栈内元素都是递增的，如果读入元素小于栈顶元素，因为栈内是递增的，所以我们就二分查找栈内第一个大于它的数，并替换它。最长序列长度即为最后模拟的大小
对于i和j，如果i <j且a[i] < a[j],用a[i]替换a[j]，长度虽然没有改变但a的’潜力’增大了。

代码：

#include <iostream>
using namespace std;
int i,j,n,s,t,a[100001];
int main()
{cin>>n;a[0]=-1000000;for(i=0;i<n;i++){cin>>t;if(t>a[s]) a[++s]=t;else{int l=1,h=s,m;while(l<=h){m=(l+h)/2;if(t>a[m]) l=m+1;else h=m-1;}a[l]=t;}}cout<<s<<endl;
}