数据结构之树,介绍篇
树的基本定义
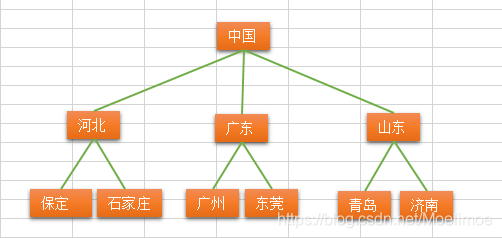
- 介绍:树(tree)是计算机中非常重要的数据结构,它的外形看起来像一颗倒挂着的的树,使用树这种结构可以描述生活中很多的事物,如族谱,单位的组织架构,xml,html的中属性的关系,文件目录,路由协议,某些数据库的索引,机器学习中的决策树等
- 定义:树是由n(n>=1)个有限结点(node)组成的一个具有层次关系的集合,某些结点之前存在特定的关系,用连线相连,连线称作边(edge),边的上端的结点称为父结点,下面的端点称为子结点
树的特点
- 每个结点有0个或多个子结点
- 没有父结点的结点称为根结点
- 一个父结点可能有多个子结点
- 每个结点及其后代结点也可以看做一棵树,称为当前结点父结点的一颗子树
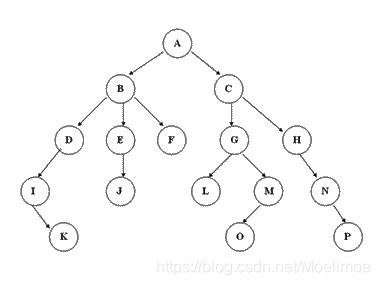
树的相关术语
- 结点的度:一个结点含有的子树的棵数
- 叶结点:度为0的结点称为叶结点,也叫做终端结点
- 分支结点:度不为0的结点称为分支结点,或叫做非终端结点
- 结点的层次:根结点层次为1,它的直接后继层次为2,以此类推
- 结点的层序编号:将一棵树的结点按照从上往下,同层次从左往右的顺序,依次使用自然数按顺序编号获得的值
- 树的度:树中所有结点最大的度,可能是根结点的度也可能不是(如某颗子树存在更多个颗树)
- 树的高度或深度:树中结点的最大层次
- 结点的深度:是指对应结点到根结点路径长度(经过的层次)
- 森林:没有相互直接连接或间接连接关系的树的集合,可称之为森林。(将一棵树的根结点及其边移除得到所有其子树组成的集合,可称为森林)
- 孩子(子)结点:一个结点的直接后继结点称之为该结点的孩子(子)结点
- 双亲(父)结点:一个结点的直接前驱结点称之为该结点的双亲(父)结点
- 兄弟结点:双亲结点相同的结点,互为兄弟结点
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
树的常见/常用种类
- 二叉树(Binary tree,区别于B-tree):每个节点最多含有两个子树的树称为二叉树;
- 完全二叉树(Complete Binary tree):除了最后一层的结点树有可能没有达到饱和外,其他所有层都已经是饱和值,此外,其最后一层的结点会尽量从左往右生成;
- 满二叉树(Full Binary tree):满二叉树是完全二叉树的一种特殊情况
- 平衡二叉树(AVL tree,取名于其两个发明者 Adelson-Velsky和Landis):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
- 二叉查找树(英语:Binary Search Tree,BST),是一种内存中特殊的数据结构,它允许对存储在其结点的数据进行增删改查,或者用作动态的数据集合,或是通过key查找对应value的查找表;
- 霍夫曼树(用于信息编码):带权路径最短的二叉树称为哈夫曼树或最优二叉树;
- B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树。
其中一部分我们会在后续详细介绍
二叉树的性质
- 性质1: 在二叉树的第i层上至多有2^(i-1)个结点(i>0)
- 性质2: 深度为k的二叉树至多有2^k - 1个结点(k>0)
- 性质3: 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1;
- 性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
- 性质5:对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外)




)
)

渲染位图)










)
