堆的排序,使用Python代码实现
上一节对堆进行了简单的实现,但是实现的堆只是部分有序(父结点大于子结点,子结点之间无序)
接下来我们实现对堆的所有元素进行升序排序
排序过程
实现步骤:
- 构造堆;
- 得到堆顶元素,这个值就是最大值;
- 交换堆顶元索和数组中的最后一个元素 ,此时所有元索中的最大元素已经放到合适的位置;
- 对堆进行调整,重新让除了最后一个元索的剩余元索中的最大值放到堆顶;
- 重复2-4这个步骤,直到堆中剩-个元索为止。
主要操作方法
- swap()交换指定两个索引的元素
- less()比较索引处元素是否第一个较小
- create_heap()创建堆,将源数组的元素copy到堆的1~length索引对应的元素处,再调用sink()方法对元素进行下沉排序
- sink()对堆中元素进行下沉排序,
- ascending_sort()对堆进行从小到大排序
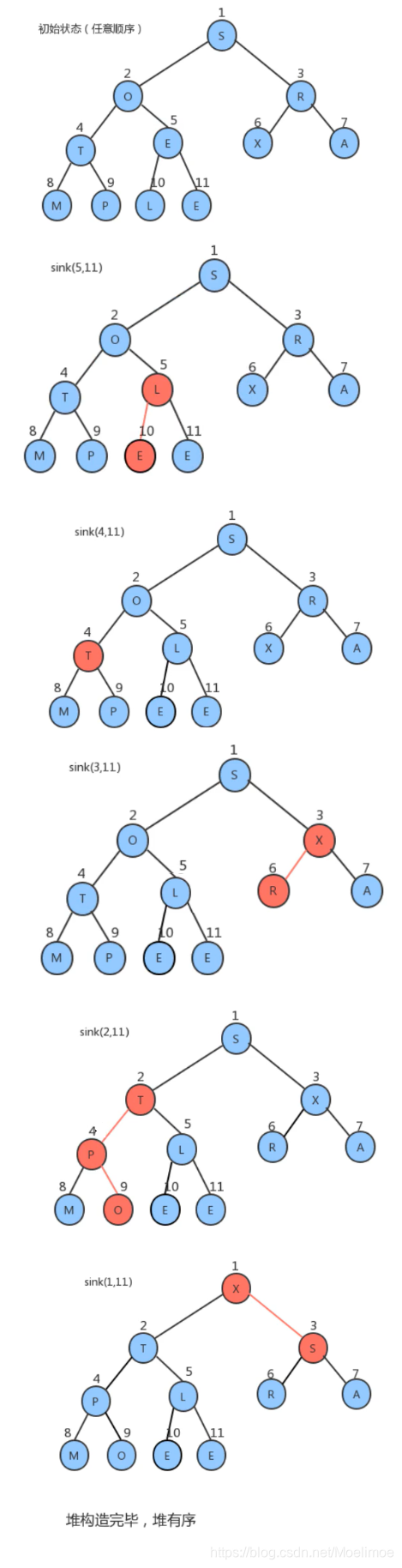
构造堆
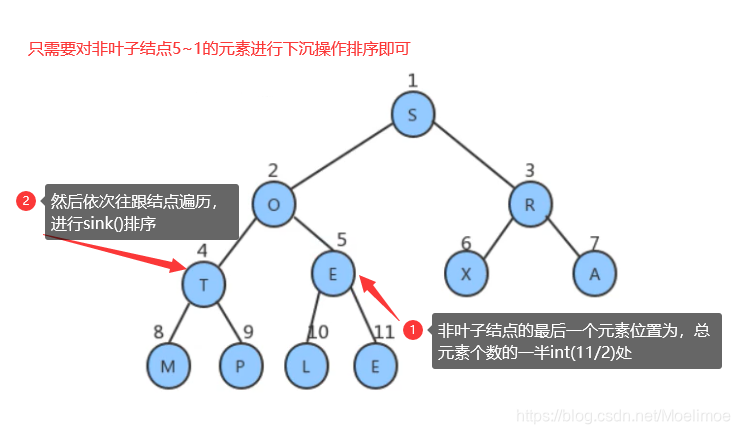
简单直观方法是对传入的无需数组从左到右遍历,然后依次将元素放入到堆的1~length处(0索引已废除,为了定位元素位置时更方便),然后对元素依次通过比较和上浮顺序调整达到堆的特性之后就实现了堆,但是我们观察堆的特性
- 堆的中间索引处就是叶子结点和非叶子结点的分割处
因此可以总结一个更简单的方法,只需要对非叶子结点做下沉动作即可:
堆构造create_heap()时的排序过程
实现堆的上升排序方法
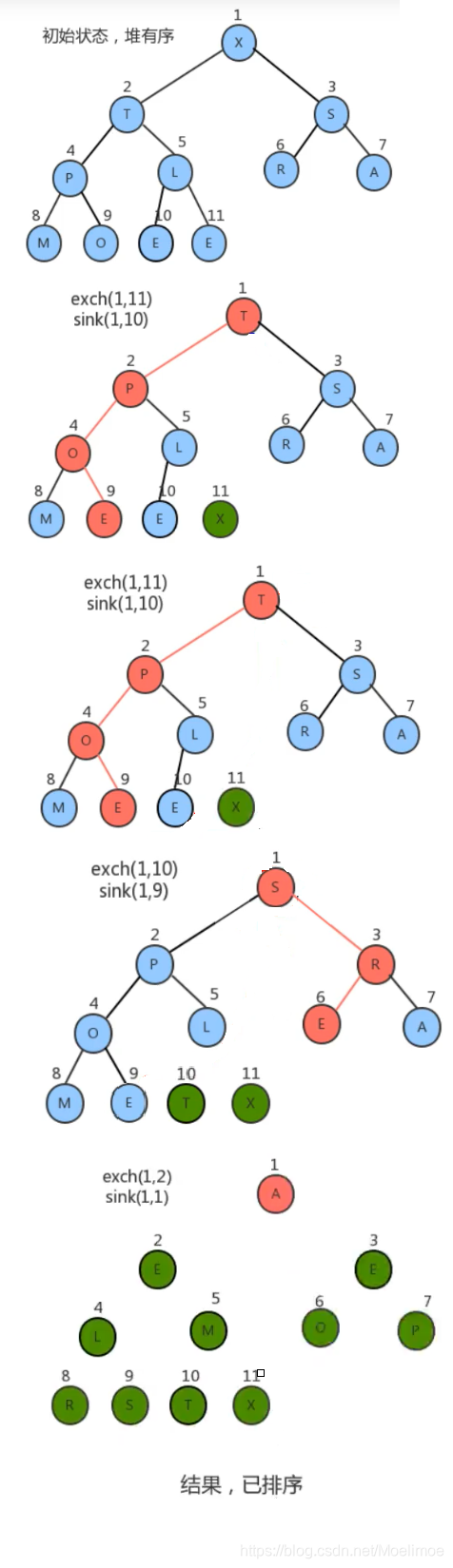
对构造好的堆, 我们只需要做类似于堆的删除操作, 就可以实现堆上升排序方法。
7. 将堆顶元素和堆中最后一个元索交换位置;
8. 通过对堆顶元索下沉调整堆,把最大的元索放到堆顶(此时最后一个元素不参与堆的调整,因为最大的数据已经到了数组的最右边)
9. 重复1-2步骤,直到堆中剩最后-个元素。
堆上升排序ascending_sort()的过程
Python代码实现
# coding = utf-8
# -*- coding:utf-8 -*-# 小根堆class HeapSort:def __init__(self):self.heap = [None] # 下标0不使用,从1开始(方便确定元素位置)self.length = 0def Swap(self, i, j):self.heap[i], self.heap[j] = self.heap[j], self.heap[i]def BuildHeap(self, target_arr):"""将传入的一维数组转变成堆"""self.heap.extend(target_arr)self.length += len(target_arr)for i in range(int((self.length-1)/2), 0, -1):self.Sink(i, self.length)def Sink(self, index, _range):"""_range是堆中最大的index,这一步实现找到左孩子和右孩子中较大者的下标"""while 2*index <= _range:# 2*index是左孩子的下标,2*index+1是右孩子的下标(若存在)max_elem_index = 2*index if 2*index+1 > _range else\(2*index + 1 if self.heap[2*index] < self.heap[2*index + 1] else 2*index)if self.heap[index] > self.heap[max_elem_index]: # 如果根结点比左孩子和右孩子都大则无需下沉,往下一个结点循环breakself.Swap(index, max_elem_index)index = max_elem_index # 若根结点(比max_index对应值还小则)下沉,还要继续比较再下一层看是否还要执行下沉def Ascending_sort(self, target_arr):"""建立小根堆,使用升序排序"""# 先建立小根堆self.BuildHeap(target_arr)N = self.lengthwhile N > 1:self.Swap(1, N)N -= 1self.Sink(1, N)if __name__ == "__main__":HS = HeapSort()# arr = ['S', 'O', 'R', 'T', 'E', 'X', 'A', 'M', 'P', 'L', 'E']arr = [122, 1, 12, 111, -5, 7, 4, 3, 56, 34, 13, 14]# arr = [7, 2, 4, 4, 3, -1, 4, 2, 8, 1]# arr = [122]HS.Ascending_sort(arr)print(HS.heap)输出结果
[None, -5, 1, 3, 4, 7, 12, 13, 14, 34, 56, 111, 122]
)













+分水岭算法+GraphCut+GrabCut)




