数据结构之平衡树：红黑树的介绍与Python代码实现——17

红黑树的介绍与Python代码实现

红黑树的介绍

红黑树(Red-Black Tree)是一种平衡二叉查找树，它是一种以比较简单的方式实现的2-3查找树

红黑树基于2-3查找树的表现

红链接:将两个2-结点连接起来构成一个3-结点 ;
黑链接:则是2-3树中的普通链接。

红黑树的定义：
红黑树是含有红黑链接并满足下列条件的二叉查找树: .

红链接均为左链接;
没有任何一个结点同时和两条红链接相连;
该树是完美色平衡的,即任意空链接到根结点的路径上的黑链接数量相同;

红黑树的优点：

一颗二叉树，每一个结点只需要额外多一位空间即可实现红黑树，这一位空间通常用于存放和表示红黑结点，而这些红黑标识则可以用来使红黑树保持接近平衡的状态
记录每一个结点的红黑状态，只需要额外的一位空间，这使得红黑树的储存空间大小在一定程度上可以认为和无颜色标记的二叉树的储存空间大小等同，在大多数情况下，无需额外的储存成本就能储存着一位的红黑记录信息
红黑树不是完美的平衡二叉树，但是它的平衡状态足够让我们能很方便地进行搜寻操作，红黑树的查询、插入、删除操作时间复杂度都是O(log n)

红黑树的平衡化

为什么需要平衡化？

在对红黑树进行一些增删改查的操作后 ,很有可能会出现红色的右链接或者两条连续红色的链接,而这些都不满足红黑树的定义,所以我们需要对这些情况通过旋转进行修复,让红黑树保持平衡。

平衡化的方法

左旋
右旋

左旋

时机：

当某个结点的左子结点为黑色,右子结点为红色,此时需要左旋。

实现方式：

当前节点为h，它的右节点是x；
color的值是由父结点指过来的线的颜色

实现过程：

在这里插入图片描述

右旋

时机：

当某个结点的左子结点是红色，并且左子结点的左子结点也是红色,要右旋

实现方式

前提:当前结点为h ,它的左子结点为x ;
color的值由父结点指过来的线的颜色

实现过程：

右旋之后保持了有序性；但是红链接连接了三个结点不满足2-3树的性质，同时违背了红黑树右链接不能为红链接的要求，这个问题下面将会介绍使用颜色反转的方法来解决

平衡步骤

向单个2-结点中插入新键后，结果是插入到该结点的右子结点，则需要进行左旋：

将c结点替换b（使b=c），b的颜色变为红，然后让b称为c的左子节点即可完成左旋（根结点的颜色后面会有一个操作让其始终保持黑色）
向底部的2-结点插入新键

情况同一，只是需要多一步，左旋之后，C的颜色要变为黑色（表示指向C的边为红色）
颜色反转

当一个结点的左子结点和右子结点的color都为RED时, 也就是出现了临时的4-结点,此时只需要把左子结点和右子结点的颜色变为BLACK ,同时让当前结点的颜色变为RED即可。
向一棵双键树(即一个3-结点)中插入新键
可分为三种子情况
4-1. 新键大于原树中的两个键：

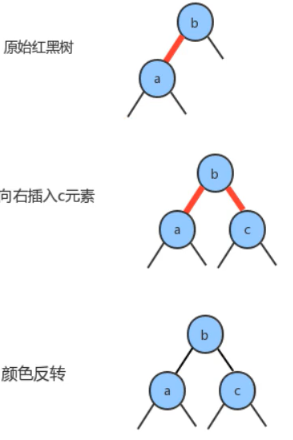
4-2. 新键小于原树中的两个键

4-3. 新键介于原数中两个键之间
根结点的颜色总是黑色
在每次放入元素的操作完成之后，将根结点的颜色变更为’Black’即可：
self.root.color = 'Black'
向树底部的3-结点插入新键

操作方法

is_red(node) 判断传入的结点node是否为红色
rotate_left(node) 将传入的结点进行左旋操作
rotate_right(node) 将传入的结点进行右旋操作
alter_color(node) 将传入的结点进行颜色反转操作
put(key, val) 插入一个键为key，值为val的元素，插入之后自动按键进行排序
get_value(key) 根据传入的键key，获取对应结点的值

Python代码实现

二叉树结点设计

class Node:def __init__(self, key, value):self.key = keyself.value = valueself.left = Noneself.right = Noneself.color = False

功能实现

class RedBlackTree:def __init__(self):self.root = Noneself.N = 0def size(self):return self.Ndef is_red(self, node):return str(node.color).lower() == 'red' if node else Falsedef rotate_left(self, node):"""Rotate left when the edge from the current node to its right child node is red"""# h is the current nodeh = node# x is the current node's right childx = node.righth.right = x.leftx.left = hx.color = h.colorh.color = 'Red'return xdef rotate_right(self, node):"""Rotate right when both the left edge and the left child's left edge are red"""h = nodex = node.lefth.left = x.rightx.right = hx.color = h.colorh.color = 'Red'return xdef alter_color(self, node):"""Alter a node's color"""node.color = 'Red'node.left.color = 'Black'node.right.color = 'Black'def put(self, key, val):"""Put an element into this tree"""def put_into(node, key, val):if not node:return Node(key, val)# Rank the orderif key < node.key:  # Recursively to compare key with its left childnode.left = put_into(node.left, key, val)elif key > node.key:node.right = put_into(node.right, key, val)else:   # Swap their the node.value with valnode.value = valreturn node# Rotation or alter colorif self.is_red(node.right) and not self.is_red(node.left):# Rotate leftself.rotate_left(node)if self.is_red(node.left) and self.is_red(node.left.left):# Rotate rightself.rotate_right(node)if self.is_red(node.left) and self.is_red(node.right):# Alter colorself.alter_color(node)self.N += 1return nodeself.root = put_into(self.root, key, val)self.root.color = 'Black'return self.rootdef get(self, key):"""Get a value according to the given key"""def get_value(node, key):if not node:returnif key < node.key:return get_value(node.left, key)elif key > node.key:return get_value(node.right, key)else:return node.valueval = get_value(self.root, key)return val

代码测试

if __name__ == '__main__':RBT = RedBlackTree()RBT.put(1, 'G')RBT.put(2, 'K')RBT.put(3, 'd')RBT.put(3, 'D')for i in range(1, 4):print(RBT.get(i), end=' ')print('\n', RBT.size())print(RBT.root.color)print(RBT.root.key, RBT.root.value)print(RBT.root.right.key, RBT.root.right.value)print(RBT.root.right.right.key, RBT.root.right.right.value)