传送门

前言

斜率优化dp，就是利用斜率优化的dp

（逃）

解析

第一道斜优的题
分析题目
设$su{m}_i$为1-i的c的前缀和
容易写出dp转移式：
$$d{p}_i=min(d{p}_j+(su{m}_i-su{m}_j+i-j-1-L{)}^2)$$

但是平方转移会T掉
考虑优化
设：
$$a_i=su{m}_i+i$$
$$b_i=su{m}_i+i+1+L$$
注意到对于固定的 i，a和b都是可求的定值
那么上面的dp，就可以写成：
$$d{p}_i=min(d{p}_j+(a_i-b_j{)}^2)$$
把平方拆开：
$$d{p}_i=min(d{p}_j+a_i^2+b_j^2-2\ast a_i\ast b_j)$$
为了转移优化，我们需要移一下项：
$$2\ast a_i\ast b_j+d{p}_i-a_i^2=d{p}_j+b_j^2$$

上面那个式子可以看成一个以$b_j$为未知数，斜率为$2\ast a_i$，且经过$(b_j,d{p}_j+b_j^2)$的一次函数
没明白？这么看：
$$f(x)=2\ast a_i\ast x+d{p}_i-a_i^2$$
$$f(b_j)=d{p}_j+b_j^2$$
$d{p}_i$就是这个函数与y轴的截距加上$a_i$的平方，因此我们实际上就是要使函数在y轴上的截距最小
有了这个函数之后，我们就可以开始尝试优化了

对于每一个新的要求的dp[i]，其直线对应的斜率是固定的
我们维护一个可以作为转移点的队列，其中的决策点对应的点对(b[x],dp[x]+b[x]^2)形成一个凸包的结构

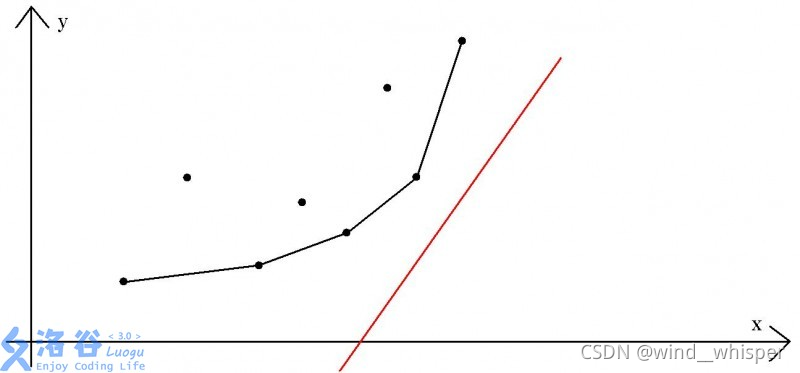
由于随着 i 的增大，其直线的斜率（$2\ast a_i$）单调递增，所以位于凸包上方的点是一定不会作为最优决策点的
若记A、B两点之间的斜率为slope（A、B）
不难看出，要使其这条直线的y轴截距最小，我们应该找到**第一个
$slope（P[j],P[j+1])>2\ast ai$ 的位置
而且由于斜率单调递增，P_j左侧的点以后一定不会再被选到了
所以我们可以用一个单调队列来维护
时间复杂度降为O(n)

代码

#include<bits/stdc++.h>
#define I register int
using namespace std;
#define ll long long
const int N=5e4+10;
ll read(){ll x=0,f=1;char c=getchar();while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}while(isdigit(c)){x=x*10+c-'0';c=getchar();}return x*f;
}
int n;
ll sum[N],c[N],a[N],b[N],l,dp[N];
struct pos{ll x,y;int pl;
};
pos q[N];
int st,ed;
double slope(pos u,pos v){return 1.0*(v.y-u.y)/(v.x-u.x);
}
int main(){
//	freopen("a.in","r",stdin);
//	freopen("a.out","w",stdout);n=read();l=read();for(int i=1;i<=n;i++){//printf("ok i=%d\n",i);c[i]=read();sum[i]=sum[i-1]+c[i];a[i]=sum[i]+i;b[i]=sum[i]+i+l+1;}b[0]=l+1;st=ed=1;q[1]={b[0],b[0]*b[0],0};for(int i=1;i<=n;i++){ll k=2*a[i];while(st<ed&&slope(q[st],q[st+1])<k) st++;ll x=q[st].x,y=q[st].y;int pl=q[st].pl;dp[i]=y+a[i]*a[i]-2*a[i]*b[pl];//printf("i=%d st=%lld dp=%lld k=%lld\n  ",i,q[st].pl,dp[i],k);//for(int i=st;i<=ed;i++) printf("%d:(%lld %lld %lld)  ",i,q[i].x,q[i].y,q[i].pl);//printf("\n\n");pos now=(pos){b[i],dp[i]+b[i]*b[i],i};while(st<ed&&slope(q[ed-1],q[ed])>slope(q[ed-1],now)){ed--;//	printf("ou2!\n");}q[++ed]=now;}printf("%lld",(long long)dp[n]);return 0;
}
/*
6 10
5
8
5
10
19
1
*/