Sky Garden

题意：

画n个圆和m条直线，圆的中心点为(0,0)，圆的半径分别从1到n，而直线都必经过(0,0)点，并且所有直线会把每个圆平均分成2m个面积相等的区域，直线会和圆形成交点，求所有交点两两经过线的最短路径的和。

题解：

因为题目多圆，多线，所以我们分类讨论
情况一：对于一个圆上的两个点，他们之间的最短距离是圆弧的长度或者是两者到圆心的距离和，即图中的粉色和绿色部分

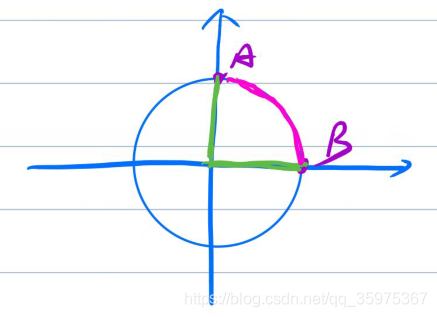
情况二：对于不是一个圆上的两个点A和B，他们之间的最短距离是从外圈圆B通过直线到内圈圆C，然后C到A的最短距离
如图

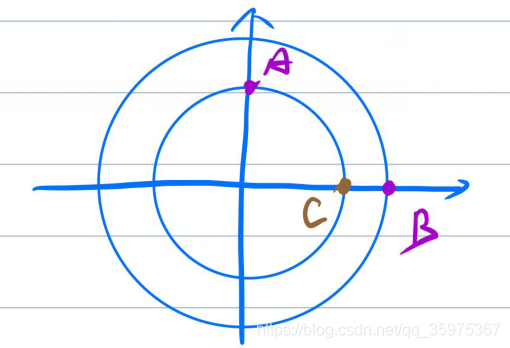
具体步骤：
1… 我们首先要计算中心交点到个点的距离和，对于半径为i的圆上交点A，A到圆心的距离为A，一共n个圆，距离就是1+…+n = n * (1+n)/2,然后有m条直线，也就是2 * m个从原点延伸的方向，每个方向都是这种情况，所以答案就是 n * (1+n) * m
2. 我们要按照从内圆到外圆的方式来计算，每此执行都用sum来记录圆内某点到其他点（其他共2 * m -1个）的距离和。图一A到B的圆心距离和为i+i，（i为第i个圆，半径也就是i），圆弧距离为 2 * pi * i * (j/2m), 2 * pi * i 好理解就是圆的周长，后面这个(j/2m)是什么意思？因为圆被分为2m份，有2 * m个射线，j表示一侧的第j+1个边，我们考虑第一个线和第j+1个线之间的圆弧情况。然后（pi * i * j）和2 * i比较大小选择即可
图中的三个绿色弧线，分别表示j=1,2，3
我们求完一侧后，根据对称性另一侧也就知道了，所以前两个弧*2再加上最后一段弧（因为左侧只需要考虑两个点）
对于第一个射线是这么考虑，一共2 * m个射线 ，sum要乘2m

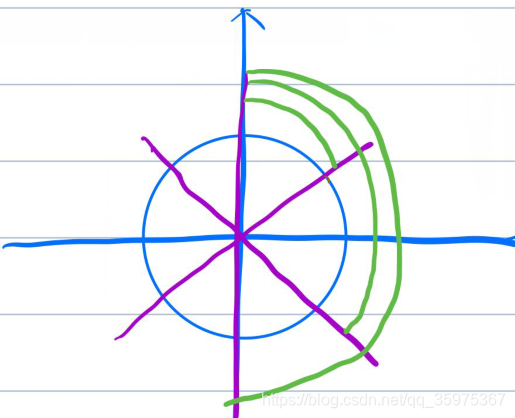
，但是这样是存在重复的，我们考虑第一条射线（绿色）和第二条射线（紫色），发现蓝色画圈部分是重复计算的，同理其他射线也是如此。相当于绿色部分的边（除了最长的那个半圆边）都重复了2 * m次，最长的那个半圆边重复了m次，所以记得减去

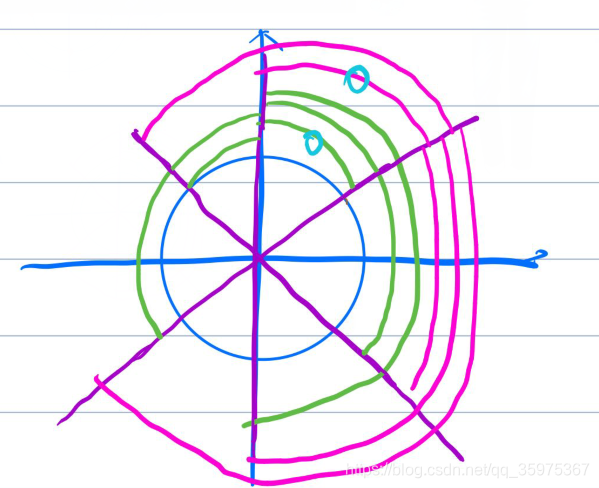
完成圆内计算后，就需要计算圆内各点到外层圆上各点的最短距离和，我们根据情况二得到圆内某个点到达外层圆上的所有点的距离和为m * (1+(n-i)) * (n-i)+sum * (n-i)，
m * (1+(n-i)) * (n-i)是当前第i层圆上某点到达外层圆上各点时走到直线上的路程，图二中C到B的过程
式子是怎么得到的：
从C到B再往外，距离是1+…+n-i
求和然后乘2m就是m * (1+(n-i)) * (n-i)
sum * (n-i)则计算的是圆内某点到达外层圆上各点投影到当前圆上各点的距离和，也就是图二中A到C的过程
最后要乘2m
这个题说简单简单，说难也难。。。
好好考虑考虑

代码：

#include<bits/stdc++.h>
using namespace std;
const double pi = acos(-1);int main()
{int n,m;scanf("%d %d",&n,&m);double ans=0;if(m!=1) ans=ans+(1+n)*n*m;for(int i=1;i<=n;i++){double sub=0;double sum=0;for(int j=1;j<=m;j++){if(j==m){sub=sub+m*2*i;sum=sum*2+2*i;}else{if((pi*i*j)/m<2*i){sum=sum+(pi*i*j)/m;sub=sub+2*m*((pi*i*j)/m);}else{sum=sum+2*i;sub=sub+2*m*2*i;}}}ans+=sum*2*m-sub;ans=ans+(m*(1+(n-i))*(n-i)+sum*(n-i))*2*m;}printf("%.10f\n",ans);return 0;
}