综合了自己在网上看到的众多博客，多种多样，肯定有很多问题，欢迎各位Dalao指出

网络流的相关概念

流网络(flow network)

流网络$G=(V,E)$是一个有向图，其中每条边$(u,v)$均有一非负容量$c(u,v)\ge 0$
流网络中有两个特殊的顶点: 源点s和汇点t
假定每个顶点都处于从源点到汇点的某条路径上，就是说，对每个顶点v，存在一条路径$s\to v\to t$
$G$为连通图，且$|E|\ge |V|-1$

流(flow)

边的流是一个实值函数f，满足下列三个性质：
容量限制：对所有$u,v\in V$， 要求$f(u,v)\le c(u,v)$
理解：流量不会超过边的容量
斜对称性：对所有$u,v\in V$， 要求$f(u,v)=-f(v,u)$
理解：一个方向的流是其反方向流的相反数。这是完善的网络流理论
不可缺少的，像用正负数来定义物理量一样。
流守恒性：对所有$u,v\in V-s,t$，要求${\sum }_{v}f(u,v)-{\sum }_{w}f(w,u)=0$
理解：进入点u的总流量=离开点u的总流量

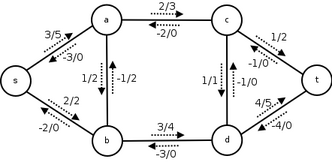
每条边上斜线前的数字是流量，后的数字是容量

网络的流

网络的流定义为$f=\sum f(s,v)$
即，从源点s出发的总流

最大流问题就是给出一个源点和汇点的流网络，希望找到从源点到汇点的最大值流

规定$f(u,v)$和$f(v,u)$最多只有一个正数（可以均为0）。若两个均为正数，可以消减一个
方向的流量
举个栗子：u给v三个苹果，v如果又给u三个苹果，那就相当于彼此之间没有给过苹果；u给v三个苹果，v给u五个苹果，就相当于v给u两个苹果。也就是说流如果都是正数，是可以相互抵消，达成协议的

残留网络(residual network)

边的残留容量：$r(u,v)=c(u,v)-f(u,v)$
残留网络一句话就是残留边所构成的一个网络流，且每条边的容量是严格为正的，即当$0<f(u,v)<c(u,v)=>r(u,v)=c(u,v)-f(u,v)>0$，这条边$(u,v)$仍在残留网络中
👉
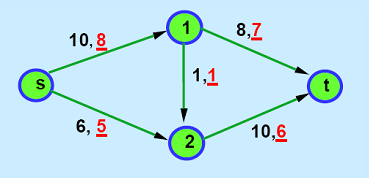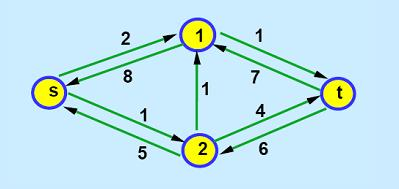
顶点1到2已经满流，故1到2的残留容量为0，但此时仍存在2到1的残留容量

增广路径(augmenting path)

增广路径P为残留网络中从源点s到汇点t的一条简单路径
增广路径的残留容量是：
$\delta (p)=minr(u,v):(u,v)\in P$
一句话就是这一条路径上最小的边流量
沿着路径增广是沿着路径的每条边发送$\delta (P)$单位的流。相应的，修改这一路径上的流的值和残留容量
$f=f+\delta (P)$
$r(u,v)=r(u,v)-\delta (P)$ $(u,v)\in P$
$r(v,u)=r(v,u)+\delta (P)$ $(u,v)\in P$

---

接下来的各个算法介绍的模板是基于luogu这道题的AC代码，一定注意哦~~

Edmonds-Karp

算法思想

Edmonds–Karp算法是一种实用性很强的，实现简洁的，基于增广路思想的网络流算法。
它的基本算法思想是：每次都找长度最短的增广路径

网络图的边可看成长度均为1，因此可用BFS找从源点s到汇点t的最短路径。
为了便于算出路径的残留容量，用一个数组$aug[v]$记录从源点s到当前结点v这条路径的残留容量
在BFS时，从队首结点u扩展出邻接点v，则有：$aug[v]=min(aug[u],cap[u][v])$，$cap[u][v]$表示$(u,v)$这一条边的残留容量
显然，BFS找出的一条增广路径的残留容量为$aug[t]$

在找到一条增广路径的过后就要更新新的残留容量

bfs模板

此代码中的flow即是上文中的aug

int BFS ( int s, int t ) {//使用BFS寻找增广路径 while ( ! q.empty() )q.pop();memset ( pre, -1, sizeof ( pre ) );pre[s] = 0;flow[s] = INF;//初始化源点的流量设为无穷大 q.push( s );while ( ! q.empty() ) {int u = q.front();q.pop();if ( u == t )//抵达汇点，找到了增广路径 break;for ( int i = 1;i <= t;i ++ ) {//遍历所有的点 //原图是没有流向s的流，但是在剩余网络中有反向边，故有流向s的流，所以要判断 if ( i != s && r[u][i] > 0 && pre[i] == -1 ) {pre[i] = u;//记录前驱以保存路径 flow[i] = min ( r[u][i], flow[u] );//迭代地找到增量 q.push( i );}}}if ( pre[t] == -1 )//汇点没有前驱节点，即残余图中无增广路径 return -1;return flow[t];
}

调用EK&更新残留网络流模板

int EK ( int s, int t ) {int max_flow = 0;int Flow = BFS ( s, t );while ( Flow != -1 ) {for ( int i = t;i != s;i = pre[i] ) {//利用前驱寻找路径，做到更新残留图 r[pre[i]][i] -= Flow;//改变正向边的容量 r[i][pre[i]] += Flow;//改变反向边的容量 }max_flow += Flow;Flow = BFS ( s, t ); }return max_flow;
}

---

luogu的AC代码(EK版)

#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
#define MAXN 405
#define INF 0x7f7f7f7f
queue < int > q;
int n, m;
int r[MAXN][MAXN];//记录残余网络的容量 
int flow[MAXN];//标记从源点到当前节点实际还剩多少流量 
int pre[MAXN];//节点的前驱，同时标记点是否被标记过 int BFS ( int s, int t ) {//使用BFS寻找增广路径 while ( ! q.empty() )q.pop();memset ( pre, -1, sizeof ( pre ) );pre[s] = 0;flow[s] = INF;//初始化源点的流量设为无穷大 q.push( s );while ( ! q.empty() ) {int u = q.front();q.pop();if ( u == t )//抵达汇点，找到了增广路径 break;for ( int i = 1;i <= t;i ++ ) {//遍历所有的点 //原图是没有流向s的流，但是在剩余网络中有反向边，故有流向s的流，所以要判断 if ( i != s && r[u][i] > 0 && pre[i] == -1 ) {pre[i] = u;//记录前驱以保存路径 flow[i] = min ( r[u][i], flow[u] );//迭代地找到增量 q.push( i );}}}if ( pre[t] == -1 )//汇点没有前驱节点，即残余图中无增广路径 return -1;return flow[t];
}int EK ( int s, int t ) {int max_flow = 0;int Flow = BFS ( s, t );while ( Flow != -1 ) {for ( int i = t;i != s;i = pre[i] ) {//利用前驱寻找路径，做到更新残留图 r[pre[i]][i] -= Flow;//改变正向边的容量 r[i][pre[i]] += Flow;//改变反向边的容量 }max_flow += Flow;Flow = BFS ( s, t ); }return max_flow;
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {int si, ei, ci;scanf ( "%d %d %d", &si, &ei, &ci );r[si][ei] += ci;}printf ( "%d", EK ( 1, m ) );return 0;
}

---

Dinic

算法思路

1、建立网络（包括正向弧和反向弧（初始边权为0）），将总流量置为0
2、构造层次网络
层次网络，简单的说，就是求出每个点u的层次，u的层次是从源点到该点的最短路径（注意：这个最短路是指弧的权都为1的情况下的最短路），若与源点不连通，层次置为-1，只用一遍bfs即可
3、判断汇点的层次是否为-1
是：算法结束，输出当前的总流量
否：下一步
4、用一次dfs实现所有增广
增广：通过dfs找的增广路，找到了之后，将每条边的权都减去该增广路中拥有最小流量的边的流量，将每条边的反向边的权增加这个值，同时将总流量加上这个值
dfs直到找不到一条可行的从原点到汇点的路
5、重复步骤2

---

细节处理，如果不是用二维结构体以下标来表示边，而是一维数组以边的编号为下标
如何快速找到一条边的反向边：边的编号从0开始，反向边加在正向边之后，反向边即为该点的编号异或1
我提供的代码里是以2开始的，写法问题，别介意
复杂度：理论上来说，应该是$O(n^2\ast m)$，n表示点数，m表示边数，然而实际上，很难卡到那个复杂度

---

弧优化
在DFS的时候记录当前已经计算到第几条边了，避免重复计算
然后在下一次构建层次网络的注意将head数组还原
温馨提醒：我们所说的Dinic时间复杂度是建立在运用了弧优化的基础上，所以如果你不用弧优化，这个时间复杂度就。。。

时间复杂度证明

与最短增广路算法一样，Dinic算法最多被分为n个阶段，每个阶段包括建层次网络和寻找增广路两部分，其中建立层次网络的复杂度仍是O（n*m)

现在来分析DFS过程的总复杂度。在每一阶段，将DFS分成两部分分析

（1）修改增广路的流量并后退的花费
在每一阶段，最多增广m次，每次修改流量的费用为$O(n)$。而一次增广后在增广路中后退的费用也为$O(n)$。所以在每一阶段中，修改增广路以及后退的复杂度为$O(m\ast n)$

（2）DFS遍历时的前进与后退
在DFS遍历时，如果当前路径的最后一个顶点能够继续扩展，则一定是沿着第i层的顶点指向第i+1层顶点的边向汇点前进了一步。因为增广路经长度最长为n，所以最坏的情况下前进n步就会遇到汇点。在前进的过程中，可能会遇到没有边能够沿着继续前进的情况，这时将路径中的最后一个点在层次图中删除

注意到每后退一次必定会删除一个顶点，所以后退的次数最多为n次。在每一阶段中，后退的复杂度为$O(n)$

假设在最坏的情况下，所有的点最后均被退了回来，一共共后退了n次，这也就意味着，有n次的前进被“无情”地退了回来，这n次前进操作都没有起到“寻找增广路”的作用。除去这n次前进和n次后退，其余的前进都对最后找到增广路做了贡献。增广路最多找到m次。每次最多前进n个点。所以所有前进操作最多为n+m*n次，复杂度为$O(n\ast m)$

于是得到，在每一阶段中，DFS遍历时前进与后退的花费为$O(m\ast n)$

综合以上两点，一次DFS的复杂度为$O(n\ast m)$。因此，Dinic算法的总复杂度即$O(m\ast n\ast n)$

bfs模板

模板1

bool bfs ( int s, int t ) {memset ( dep, 0, sizeof ( dep ) );dep[s] = 1;while ( !q.empty() )q.pop();q.push( s );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = 1;i <= m;i ++ ) {if ( ! dep[i] && edge[u][i].c > edge[u][i].flow ) { dep[i] = dep[u] + 1;q.push( i );}}}return dep[t] != 0;
}

模板2

bool bfs ( int s, int t ) {memcpy ( cur, head, sizeof ( head ) );memset ( dep, 0, sizeof ( dep ) );dep[s] = 1;while ( !q.empty() )q.pop();q.push( s );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].to;if ( ! dep[v] && edge[i].flow ) {//有流量就增广 dep[v] = dep[u] + 1;q.push( v );}}}return dep[t] != 0;
}

dfs模板

不带弧优化模板（最好别用）

int dfs ( int now, int t, int cap ) {if ( now == t ) return cap;int tmp = cap, flow;for ( int i = 1;i <= m && tmp;i ++ ) {if ( dep[i] == dep[now] + 1 && edge[now][i].c > edge[now][i].flow) {flow = dfs ( i, t, min ( tmp, edge[now][i].c - edge[now][i].flow ) );edge[now][i].flow += flow;edge[i][now].flow -= flow;tmp -= flow;}}return cap - tmp;
}

带弧优化模板

int dfs ( int now, int t, int cap ) {//分别是当前点，汇点，当前边上最小的流量 if ( ! cap || now == t )//终止条件，要么这条路断了，要么走到了汇点 return cap;int flow = 0;for ( int i = cur[now];i;i = edge[i].next ) {//开始弧优化 cur[now] = i;//记录一下遍历到了哪里 int v = edge[i].to;if ( dep[v] == dep[now] + 1 ) {//分层图，只能往下找一层 int tmp = dfs ( v, t, min ( cap, edge[i].flow ) );if ( ! tmp )//如果tmp=0就意味着找不到增广路了 continue;flow += tmp;cap -= tmp;edge[i].flow -= tmp;edge[i ^ 1].flow += tmp;//处理反向边 if ( ! cap ) //没有残量就意味着没有增广路了 break;}}return flow;
}

---

献上我丑陋的代码。。。

不带弧优化版AC代码

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define INF 0x7f7f7f7f
#define MAXN 205
struct node {int c, flow;
}edge[MAXN][MAXN];
queue < int > q;
int n, m, cnt = 1;
int dep[MAXN];bool bfs ( int s, int t ) {memset ( dep, 0, sizeof ( dep ) );dep[s] = 1;while ( !q.empty() )q.pop();q.push( s );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = 1;i <= m;i ++ ) {if ( ! dep[i] && edge[u][i].c > edge[u][i].flow ) { dep[i] = dep[u] + 1;q.push( i );}}}return dep[t] != 0;
}int dfs ( int now, int t, int cap ) {if ( now == t ) return cap;int tmp = cap, flow;for ( int i = 1;i <= m && tmp;i ++ ) {if ( dep[i] == dep[now] + 1 && edge[now][i].c > edge[now][i].flow) {flow = dfs ( i, t, min ( tmp, edge[now][i].c - edge[now][i].flow ) );edge[now][i].flow += flow;edge[i][now].flow -= flow;tmp -= flow;}}return cap - tmp;
}int dinic ( int s, int t ) {int flow = 0;while ( bfs( s, t ) )flow += dfs ( s, t, INF );return flow;
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {int si, ei, ci;scanf ( "%d %d %d", &si, &ei, &ci );edge[si][ei].c += ci;}printf ( "%d", dinic ( 1, m ) );return 0;
} 

带弧优化AC代码

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define INF 0x7f7f7f7f
#define MAXN 205
struct node {int next, to, flow;
}edge[MAXN << 1];
queue < int > q;
int n, m, cnt = 1;
int head[MAXN], cur[MAXN], dep[MAXN];
//dep记录bfs分层图每个点到源点的距离 
void add ( int x, int y, int w ) {cnt ++;edge[cnt].next = head[x];edge[cnt].to = y;edge[cnt].flow = w;head[x] = cnt;
}bool bfs ( int s, int t ) {memcpy ( cur, head, sizeof ( head ) );memset ( dep, 0, sizeof ( dep ) );dep[s] = 1;while ( !q.empty() )q.pop();q.push( s );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].to;if ( ! dep[v] && edge[i].flow ) {//有流量就增广 dep[v] = dep[u] + 1;q.push( v );}}}return dep[t] != 0;
}int dfs ( int now, int t, int cap ) {//分别是当前点，汇点，当前边上最小的流量 if ( ! cap || now == t )//终止条件，要么这条路断了，要么走到了汇点 return cap;int flow = 0;for ( int i = cur[now];i;i = edge[i].next ) {//开始弧优化 cur[now] = i;//记录一下遍历到了哪里 int v = edge[i].to;if ( dep[v] == dep[now] + 1 ) {//分层图，只能往下找一层 int tmp = dfs ( v, t, min ( cap, edge[i].flow ) );if ( ! tmp )//如果tmp=0就意味着找不到增广路了 continue;flow += tmp;cap -= tmp;edge[i].flow -= tmp;edge[i ^ 1].flow += tmp;//处理反向边 if ( ! cap ) //没有残量就意味着没有增广路了 break;}}return flow;
}int dinic ( int s, int t ) {int flow = 0;while ( bfs( s, t ) )flow += dfs ( s, t, INF );return flow;
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {int si, ei, ci;scanf ( "%d %d %d", &si, &ei, &ci );add ( si, ei, ci );add ( ei, si, 0 );}printf ( "%d", dinic ( 1, m ) );return 0;
} 

ISAP

算法思想

我们达到如下目标：
能在O(n)时间内判断每次增广，如果我们维持“距离标号”且能在O(n)时间内实施增广.
维持和更新所有距离标号的总时间是O(mn).
总增广数是O(nm).
结论：总运行时间是O(n^2m)

---

距离标号
距离标号是一个函数：$d:V\to Z+$. 距离标号被称为是有效，如果它满足以下:
$d(t)=0$ //汇点的标号为0
$d(i)\le d(j)+1$ 对每个 $(i,j)\in G(f)$
边 $(i,j)\in G(f)$ 是可进入的，前提是如果 $d(i)=d(j)+1$.

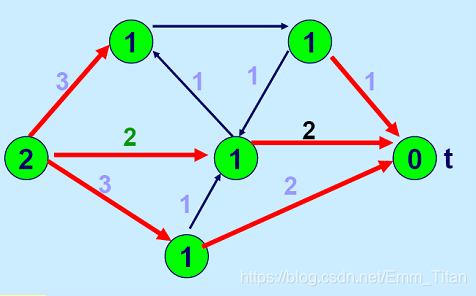
顶点里的数字是各顶点的距离标号。红色边是残留网络中的可进入弧。可以发现，可进入弧的数量是少于图中总的边数的，为找增广路节约了时间

---

实现
理论上初始距离标号要用反向BFS求得，实践中可以全部设为0，可以证明：这样做不改变渐进时间复杂度。
理论上可以写出许多子程序并迭代实现，但判断琐碎，没有层次，实践中用递归简单明了
GAP优化：注意到我们在某次增广后，最大流可能已经求出，因后算法继续重标号，做了许多无用功。可以发现，距离标号是单调增的。这启示我们如果标号中存在“间隙”，则图中不会再有增广路，于是算法提前终止。
实践中我们使用数组vd[i]记录标号为i的顶点个数，若重新标号使得vd中原标号项变为0，则停止算法（出现了断层） 不必在每次增广后实时更新图中的流量，可以让一条增广路有多个分叉并统计增广量，在算法前进与回溯的执行过程中自动更新流量

bfs模板

void bfs () {//初始化bfs，从t到s搜出每个点初始深度 memset ( dep, -1, sizeof ( dep ) );memset ( gap, 0, sizeof ( gap ) );while ( ! q.empty() )q.pop();dep[t] = 0;gap[0] = 1;q.push( t );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].v;if ( dep[v] != -1 )continue;q.push( v );dep[v] = dep[u] + 1;gap[dep[v]] ++;}}
}

dfs模板

不带弧优化

int dfs ( int u, int flow ) {if ( u == t ) {maxflow += flow;return flow;}int used = 0;for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].v;if ( edge[i].flow && dep[v] + 1 == dep[u] ) {//为什么不是dep[v]==dep[u]+1，请注意我们bfs是从t倒着的，自然而然dep也倒着了 int tmp = dfs ( v, min ( edge[i].flow, flow - used ) );if ( tmp ) {edge[i].flow -= tmp;edge[i ^ 1].flow += tmp;used += tmp;}if ( used == flow )return used;}}//如果已经到此，说明该点u出去的所有点都已经流过了//并且从前面点传过来的流量flow仍有剩余//则此时要修改该点的dep使得该点与该点出去的所有点分隔开 -- gap[dep[u]];if ( ! gap[dep[u]] )//出现断层，无法到达汇点t了 dep[s] = n + 1;dep[u] ++;gap[dep[u]] ++; return used;
}

带弧优化

int dfs ( int u, int flow ) {if ( u == t ) {maxflow += flow;return flow;}int used = 0;for ( int i = cur[u];i;i = edge[i].next ) {cur[u] = i;int v = edge[i].v;if ( edge[i].flow && dep[v] + 1 == dep[u] ) {//为什么不是dep[v]==dep[u]+1，请注意我们bfs是从t倒着的，自然而然dep也倒着了 int tmp = dfs ( v, min ( edge[i].flow, flow - used ) );if ( tmp ) {edge[i].flow -= tmp;edge[i ^ 1].flow += tmp;used += tmp;}if ( used == flow )return used;}}//如果已经到此，说明该点u出去的所有点都已经流过了//并且从前面点传过来的流量flow仍有剩余//则此时要修改该点的dep使得该点与该点出去的所有点分隔开 -- gap[dep[u]];if ( ! gap[dep[u]] )//出现断层，无法到达汇点t了 dep[s] = n + 1;dep[u] ++;gap[dep[u]] ++; return used;
}

不带弧优化版AC代码

#include <queue> 
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define MAXN 205
#define INF 0x7f7f7f7f
struct node {int v, next, flow;
}edge[MAXN << 1];
queue < int > q;
int maxflow, s, t, n, m, cnt = 1;
int dep[MAXN], gap[MAXN], head[MAXN];
//dep[i]表示节点i的深度，gap[i]表示深度为i的点的数量void add ( int x, int y, int w ) {cnt ++;edge[cnt].next = head[x];edge[cnt].flow = w;edge[cnt].v = y;head[x] = cnt;
}void bfs () {//初始化bfs，从t到s搜出每个点初始深度 memset ( dep, -1, sizeof ( dep ) );memset ( gap, 0, sizeof ( gap ) );while ( ! q.empty() )q.pop();dep[t] = 0;gap[0] = 1;q.push( t );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].v;if ( dep[v] != -1 )continue;q.push( v );dep[v] = dep[u] + 1;gap[dep[v]] ++;}}
}
//可以看出ISAP的bfs里面对边权!=0的条件没有限制，只需要再后面的dfs里进行判断即可
int dfs ( int u, int flow ) {if ( u == t ) {maxflow += flow;return flow;}int used = 0;for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].v;if ( edge[i].flow && dep[v] + 1 == dep[u] ) {//为什么不是dep[v]==dep[u]+1，请注意我们bfs是从t倒着的，自然而然dep也倒着了 int tmp = dfs ( v, min ( edge[i].flow, flow - used ) );if ( tmp ) {edge[i].flow -= tmp;edge[i ^ 1].flow += tmp;used += tmp;}if ( used == flow )return used;}}//如果已经到此，说明该点u出去的所有点都已经流过了//并且从前面点传过来的流量flow仍有剩余//则此时要修改该点的dep使得该点与该点出去的所有点分隔开 -- gap[dep[u]];if ( ! gap[dep[u]] )//出现断层，无法到达汇点t了 dep[s] = n + 1;dep[u] ++;gap[dep[u]] ++; return used;
}int ISAP () {maxflow = 0;bfs();while ( dep[s] < n )dfs ( s, INF );return maxflow;
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {int si, ei, ci;scanf ( "%d %d %d", &si, &ei, &ci );add ( si, ei, ci );add ( ei, si, 0 );}s = 1;t = m;printf ( "%d", ISAP() );return 0;
} 

带弧优化版AC代码

如果已经懂了Dinic，其实只要改一点点就好了

#include <queue> 
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define MAXN 205
#define INF 0x7f7f7f7f
struct node {int v, next, flow;
}edge[MAXN << 1];
queue < int > q;
int maxflow, s, t, n, m, cnt = 1;
int dep[MAXN], gap[MAXN], head[MAXN], cur[MAXN];
//dep[i]表示节点i的深度，gap[i]表示深度为i的点的数量void add ( int x, int y, int w ) {cnt ++;edge[cnt].next = head[x];edge[cnt].flow = w;edge[cnt].v = y;head[x] = cnt;
}void bfs () {//初始化bfs，从t到s搜出每个点初始深度 memset ( dep, -1, sizeof ( dep ) );memset ( gap, 0, sizeof ( gap ) );while ( ! q.empty() )q.pop();dep[t] = 0;gap[0] = 1;q.push( t );while ( ! q.empty() ) {int u = q.front();q.pop();for ( int i = head[u];i;i = edge[i].next ) {int v = edge[i].v;if ( dep[v] != -1 )continue;q.push( v );dep[v] = dep[u] + 1;gap[dep[v]] ++;}}
}
//可以看出ISAP的bfs里面对边权!=0的条件没有限制，只需要再后面的dfs里进行判断即可
int dfs ( int u, int flow ) {if ( u == t ) {maxflow += flow;return flow;}int used = 0;for ( int i = cur[u];i;i = edge[i].next ) {cur[u] = i;int v = edge[i].v;if ( edge[i].flow && dep[v] + 1 == dep[u] ) {//为什么不是dep[v]==dep[u]+1，请注意我们bfs是从t倒着的，自然而然dep也倒着了 int tmp = dfs ( v, min ( edge[i].flow, flow - used ) );if ( tmp ) {edge[i].flow -= tmp;edge[i ^ 1].flow += tmp;used += tmp;}if ( used == flow )return used;}}//如果已经到此，说明该点u出去的所有点都已经流过了//并且从前面点传过来的流量flow仍有剩余//则此时要修改该点的dep使得该点与该点出去的所有点分隔开 -- gap[dep[u]];if ( ! gap[dep[u]] )//出现断层，无法到达汇点t了 dep[s] = n + 1;dep[u] ++;gap[dep[u]] ++; return used;
}int ISAP () {maxflow = 0;bfs();while ( dep[s] < n ) {memcpy ( cur, head, sizeof ( head ) ); dfs ( s, INF );}return maxflow;
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ ) {int si, ei, ci;scanf ( "%d %d %d", &si, &ei, &ci );add ( si, ei, ci );add ( ei, si, 0 );}s = 1;t = m;printf ( "%d", ISAP() );return 0;
} 

肯定有很多问题，欢迎各位Dalao指出

Update(仅模板)

无源汇有上下界可行流

//LOJ 题目同名
#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
#define maxn 205
#define inf 1e9
struct node {int nxt, to, flow;
}edge[maxn * maxn];
queue < int > q;
int n, m, cnt;
int dep[maxn], head[maxn], cur[maxn], d[maxn], minn[maxn * maxn];void addedge( int u, int v, int w ) {edge[cnt].nxt = head[u];edge[cnt].to = v;edge[cnt].flow = w;head[u] = cnt ++;edge[cnt].nxt = head[v];edge[cnt].to = u;edge[cnt].flow = 0;head[v] = cnt ++;
}bool bfs( int s, int t ) {memcpy( cur, head, sizeof( head ) );memset( dep, 0, sizeof( dep ) );dep[s] = 1, q.push( s );while( ! q.empty() ) {int u = q.front(); q.pop();for( int i = head[u];~ i;i = edge[i].nxt ) {int v = edge[i].to;if( ! dep[v] && edge[i].flow ) {dep[v] = dep[u] + 1;q.push( v );}}}return dep[t];
}int dfs( int u, int t, int cap ) {if( ! cap || u == t ) return cap;int flow = 0;for( int i = cur[u];~ i;i = edge[i].nxt ) {cur[u] = i;int v = edge[i].to;if( dep[v] == dep[u] + 1 ) {int w = dfs( v, t, min( cap, edge[i].flow ) );if( ! w ) continue;cap -= w;flow += w;edge[i].flow -= w;edge[i ^ 1].flow += w;if( ! cap ) break;}}return flow;
}int dinic( int s, int t ) {int ans = 0;while( bfs( s, t ) )ans += dfs( s, t, inf );return ans;
}int main() {memset( head, -1, sizeof( head ) );scanf( "%d %d", &n, &m );int s = 0, t = n + 1, sum = 0;for( int i = 0, u, v, low, up;i < m;i ++ ) {scanf( "%d %d %d %d", &u, &v, &low, &up );d[u] -= low;d[v] += low;minn[i] = low;addedge( u, v, up - low );}for( int i = 1;i <= n;i ++ ) {if( d[i] > 0 ) {sum += d[i];addedge( s, i, d[i] );}if( d[i] < 0 )addedge( i, t, -d[i] );}if( sum != dinic( s, t ) ) printf( "NO\n" );else {printf( "YES\n" );for( int i = 0;i < m;i ++ )printf( "%d\n", edge[i << 1 | 1].flow + minn[i] );}return 0;
}
//无源汇有上下界可行流

有源汇有上下界最大流

//LOJ 题目同名
#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
#define maxn 205
#define inf 1e9
struct node {int nxt, to, flow;
}edge[maxn * maxn];
queue < int > q;
int cnt;
int head[maxn], cur[maxn], dep[maxn], d[maxn];void addedge( int u, int v, int w ) {edge[cnt].nxt = head[u];edge[cnt].to = v;edge[cnt].flow = w;head[u] = cnt ++;edge[cnt].nxt = head[v];edge[cnt].to = u;edge[cnt].flow = 0;head[v] = cnt ++;
}bool bfs( int s, int t ) {memcpy( cur, head, sizeof( head ) );memset( dep, 0, sizeof( dep ) );dep[s] = 1, q.push( s );while( ! q.empty() ) {int u = q.front(); q.pop();for( int i = head[u];~ i;i = edge[i].nxt ) {int v = edge[i].to;if( ! dep[v] && edge[i].flow ) {dep[v] = dep[u] + 1;q.push( v );}}}return dep[t];
}int dfs( int u, int t, int cap ) {if( ! cap || u == t ) return cap;int flow = 0;for( int i = cur[u];~ i;i = edge[i].nxt ) {cur[u] = i;int v = edge[i].to;if( dep[v] == dep[u] + 1 ) {int w = dfs( v, t, min( cap, edge[i].flow ) );if( ! w ) continue;cap -= w;flow += w;edge[i].flow -= w;edge[i ^ 1].flow += w;if( ! cap ) break;}}return flow;
}int dinic( int s, int t ) {int ans = 0;while( bfs( s, t ) )ans += dfs( s, t, inf );return ans;
}int main() {memset( head, -1, sizeof( head ) );int n, m, s, t;scanf( "%d %d %d %d", &n, &m, &s, &t );int ss = 0, tt = n + 1, sum = 0;for( int i = 1, u, v, low, up;i <= m;i ++ ) {scanf( "%d %d %d %d", &u, &v, &low, &up );d[u] -= low, d[v] += low;addedge( u, v, up - low );}for( int i = 1;i <= n;i ++ ) {if( d[i] > 0 ) {sum += d[i];addedge( ss, i, d[i] );}if( d[i] < 0 )addedge( i, tt, -d[i] );}addedge( t, s, inf );if( sum != dinic( ss, tt ) ) return ! printf( "please go home to sleep\n" );else printf( "%d\n", dinic( s, t ) );return 0;
}
//有源汇有上下界最大流 

有源汇有上下界最小流

//LOJ 题目同名
#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
#define int long long
#define maxn 50010
#define inf 1e18
#define maxm 400100
struct node {int nxt, to, flow;
}edge[maxm];
queue < int > q;
int cnt;
int head[maxn], cur[maxn], dep[maxn], d[maxn];void addedge( int u, int v, int w ) {edge[cnt].nxt = head[u];edge[cnt].to = v;edge[cnt].flow = w;head[u] = cnt ++;edge[cnt].nxt = head[v];edge[cnt].to = u;edge[cnt].flow = 0;head[v] = cnt ++;
}bool bfs( int s, int t ) {memcpy( cur, head, sizeof( head ) );memset( dep, 0, sizeof( dep ) );dep[s] = 1, q.push( s );while( ! q.empty() ) {int u = q.front(); q.pop();for( int i = head[u];~ i;i = edge[i].nxt ) {int v = edge[i].to;if( ! dep[v] && edge[i].flow ) {dep[v] = dep[u] + 1;q.push( v );}}}return dep[t];
}int dfs( int u, int t, int cap ) {if( ! cap || u == t ) return cap;int flow = 0;for( int i = cur[u];~ i;i = edge[i].nxt ) {cur[u] = i;int v = edge[i].to;if( dep[v] == dep[u] + 1 ) {int w = dfs( v, t, min( cap, edge[i].flow ) );if( ! w ) continue;cap -= w;flow += w;edge[i].flow -= w;edge[i ^ 1].flow += w;if( ! cap ) break;}}return flow;
}int dinic( int s, int t ) {int ans = 0;while( bfs( s, t ) )ans += dfs( s, t, inf );return ans;
}signed main() {memset( head, -1, sizeof( head ) );int n, m, s, t;scanf( "%lld %lld %lld %lld", &n, &m, &s, &t );int ss = 0, tt = n + 1, sum = 0;for( int i = 1, u, v, low, up;i <= m;i ++ ) {scanf( "%lld %lld %lld %lld", &u, &v, &low, &up );d[u] -= low, d[v] += low;addedge( u, v, up - low );}for( int i = 1;i <= n;i ++ ) {if( d[i] > 0 ) {sum += d[i];addedge( ss, i, d[i] );}if( d[i] < 0 ) addedge( i, tt, -d[i] );}int flow = 0;flow += dinic( ss, tt );addedge( t, s, inf );flow += dinic( ss, tt );if( sum != flow ) return ! printf( "please go home to sleep\n" );else printf( "%lld\n", edge[cnt - 1].flow );return 0;
}
//有源汇有上下界最小流