Walker

题意：

一个区间[0,n]，区间上有两个点，坐标分别是pos1，pos2，速度分别是v1，v2，这两个点是在移动，可以随时改变移动方向，问当区间的每一块均被一个点或两个点移动覆盖时，最少花费的时间是多少

题解：

介绍一个函数get_dis(pos,v,n)：在pos位置覆盖区间n需要的最短时间
这个最短时间由两个部分取最小值
一个部分是从pos走到0再返回到n
另一个是从pos走到n再返回到0
我们分类讨论情况：

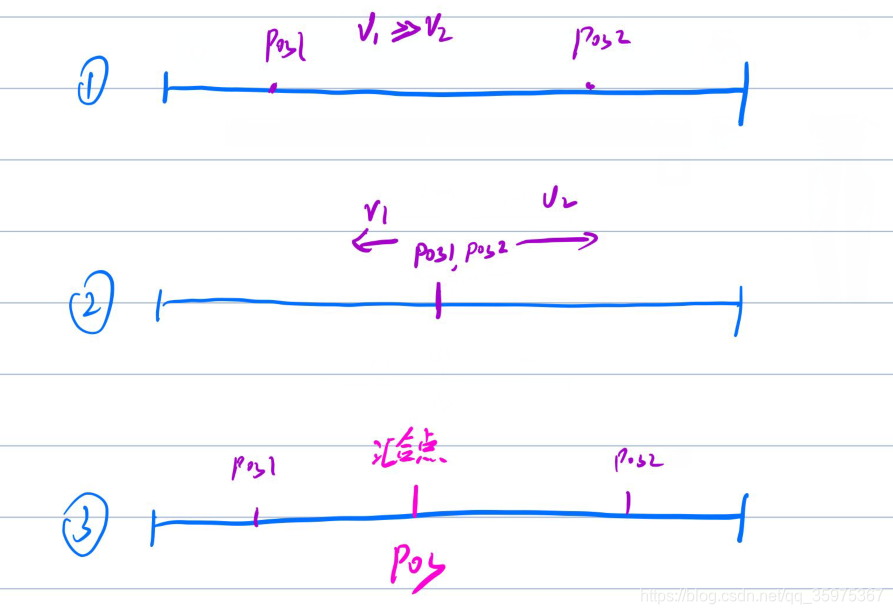
1. 当其中一点的速度>>另一点速度时，这样我们就靠一个点来跑完全程就行

	ans = min(ans , get_dis(p1,v1,n));ans = min(ans , get_dis(p2,v2,n));

2. 当两个点一开始重合时，这样可以分别往两边跑，取两者时间最大值

	ans = min(ans , max((n-p1)/v1 , p2/v2));

3. 两者相中间跑汇合后再反方向想往跑
   我们着重讲第三点，这个汇合点pos怎么确定？
   我们先想想，在第三个情况下，两者我们时间是要先取最大值，然后在最大值里选最小值，也就是两者所用时间应该越相近越好，这样可以保证最大化的最小值合理，而确定pos我们当然要用二分
   当前的mid使得前者时间大于后者时，mid就应该往左移动，所以r=mid，反之l=mid，进行个100多次二分，这个答案就会非常精确了
   以上三种情况取最小输出
   

代码：

#include <bits/stdc++.h>
using namespace std;//在pos位置覆盖到区间n需要的最短时间 
double get_dis(double pos,double v,double n)
{	double a = (pos + n) / v; // 往左走到l再走到n double b = (n - pos + n) / v; //往右走到r再走到n return min(a,b); // 取最小值 
}void Solve()
{double n,p1,v1,p2,v2;scanf("%lf%lf%lf%lf%lf",&n,&p1,&v1,&p2,&v2);if(p1 > p2){swap(p1,p2);swap(v1,v2);}double ans = 9999999999999999;// 1.自己走完全程用的时间 ans = min(ans , get_dis(p1,v1,n));ans = min(ans , get_dis(p2,v2,n));// 2.相对走完自己的路程 ans = min(ans , max((n-p1)/v1 , p2/v2));//	cout<<ans<<endl;double l = p1,r = p2; // 在p1和p2之间寻找一个分界点 for(int i=1;i<=100;i++) //  二分分界点 {double mid = (l + r) / 2; //分界点 double ans1 = get_dis(p1,v1,mid); double ans2 = get_dis(n-p2,v2,n-mid);ans = min(ans,max(ans1,ans2));if(ans1 < ans2) l = mid; // 让到达分界点的时间尽可能的相同 else r = mid;}printf("%.12f",ans);
}
int main()
{int t;scanf("%d",&t);while(t--){Solve();if(t) puts("");} 
}/*
2
10000.0 1.0 0.001 9999.0 0.001
4306.063 4079.874 0.607 1033.423 0.847
*/