标题：ASP.NET Core中实现单体程序的事件发布/订阅作者：Lamond Lu
地址：https://www.cnblogs.com/lwqlun/p/10468058.html

项目源代码：https://github.com/lamondlu/EventHandlerInSingleApplication

640?wx_fmt=png

背景

事件发布/订阅是一种非常强大的模式，它可以帮助业务组件间实现完全解耦，不同的业务组件只依赖事件，只关注哪些事件是需要自己处理的，而不用关注谁来处理自己发布事件，事件追溯(Event Sourcing)也是基于事件发布/订阅的。在微服务架构中，事件发布/订阅有非常多的应用场景。今天我给大家分享一个基于ASP.NET Core的单体程序使用事件发布/订阅的例子，针对分布式项目的事件发布/订阅比较复杂，难点是事务处理，后续我会另写一篇博文来演示。

案例说明

当前我们有一个基于ASP.NET Core的电子商务系统，在项目的初期，业务非常简单，只有一个购物车模块和一个订单模块，所有的代码都放在一个项目中。

整个项目使用了一个简单的三层架构。

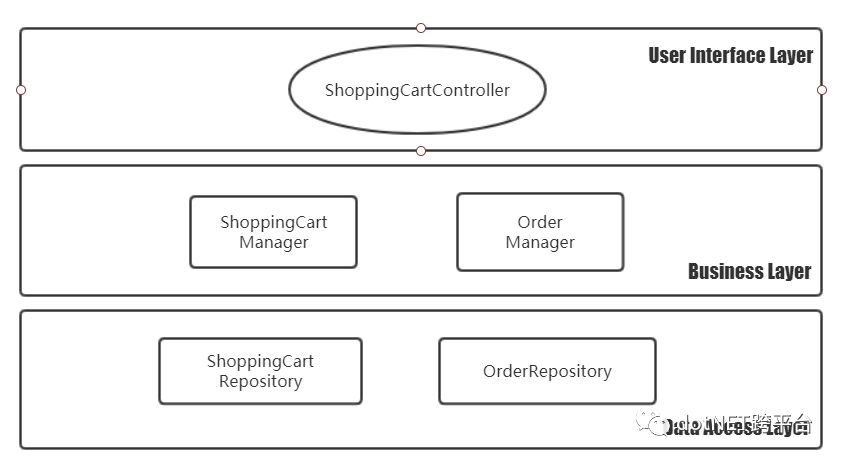
640?wx_fmt=png

这里当用户提交购物车的时候，程序会在ShoppingCartManager类的SubmitShoppingCart方法中执行3个操作

修改当前购物车的状态为完成
根据购物车中的物品创建一个新订单
给用户发邮件

代码如下：

 public void SubmitShoppingCart(string shoppingCartId) { var shoppingCart = _unitOfWork.ShoppingCartRepository .GetShoppingCart(shoppingCartId); _unitOfWork.ShoppingCartRepository .SubmitShoppingCart(shoppingCartId); _unitOfWork.OrderRepository .CreatOrder(new CreateOrderDTO { Items = shoppingCart.Items .Select(p => new NewOrderItemDTO { ItemId = p.ItemId, Name = p.Name, Price = p.Price }).ToList() }); //这里为了简化代码，我用命令行表示发送邮件的逻辑 Console.WriteLine("Confirm Email Sent."); _unitOfWork.Save(); }

根据SOLID设计原则中的单一责任原则，如果一个类承担的职责过多，就等于把这些职责耦合在一起了。这里生成订单和发送邮件都不应该是当前SubmitShoppingCart需要负责的，所以我们需要它们从这个方法中移出去，使用的方法就是事件订阅/发布。

新的架构图

以下是使用事件发布/订阅之后的系统架构图。

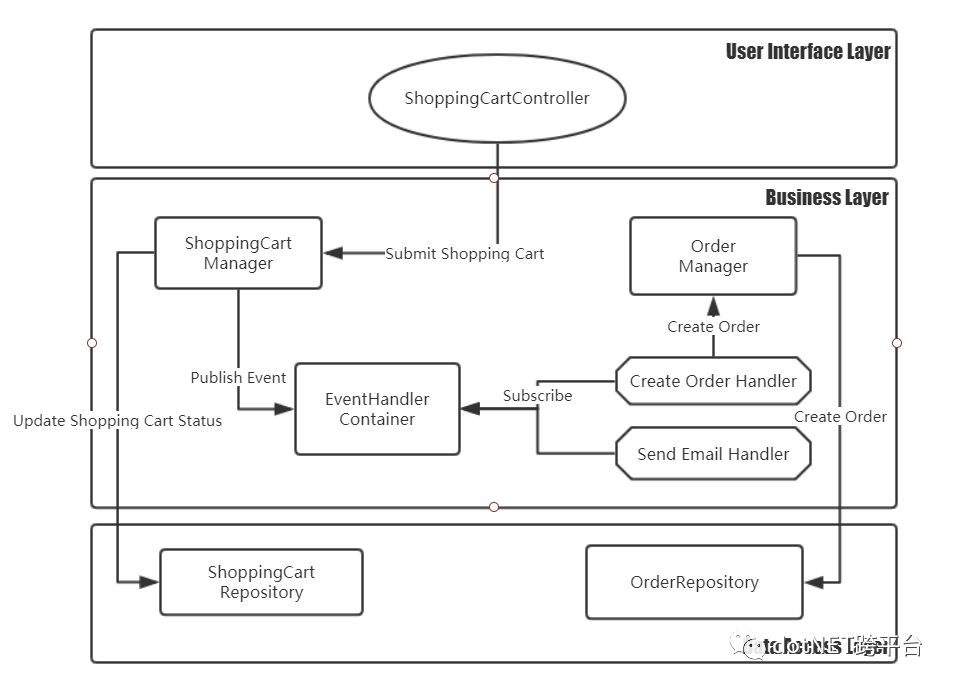
640?wx_fmt=png

这里我们会创建一个购物车提交事件ShoppingCartSubmittedEvent。
当站点启动的时候，我们会在一个名为EventHandlerContainer的类中注册订阅ShoppingCartSubmittedEvent事件的2个处理类CreateOrderHandler和ConfirmEmailSentHandler。
在SubmitShoppingCart方法中，我们会做2件事情：
- 更改当前购物车的状态。
- 发布ShoppingCartSubmittedEvent事件。
CreateOrderHandler事件处理器会调用OrderManager类中的创建订单方法。
ConfirmEmailSentHandler事件处理器会负责发送邮件。

好的，下面让我们来一步一步实现以上描述的代码。

添加事件基类

这里我们首先定义一个事件基类，其中暂时只添加了一个属性OccuredOn，它表示了当前事件的触发时间。

 public class EventBase { public EventBase() { OccuredOn = DateTime.Now; } protected DateTime OccuredOn { get; set; } }

定义购物车提交事件

接下来我们就需要创建购物车提交事件类ShoppingCartSubmittedEvent，它继承自EventBase, 并提供了一个购物项集合

 public class ShoppingCartSubmittedEvent : EventBase { public ShoppingCartSubmittedEvent() { Items = new List<ShoppingCartSubmittedItem>(); } public List<ShoppingCartSubmittedItem> Items { get; set; } } public class ShoppingCartSubmittedItem { public string ItemId { get; set; } public string Name { get; set; } public decimal Price { get; set; } }

定义事件处理器接口

为了添加事件处理器，我们首先需要定义一个泛型接口类IEventHandler

 public interface IEventHandler<T> where T : EventBase { void Run(T obj); Task RunAsync(T obj); }

这个泛型接口类的是泛型类型必须继承自EventBase类。接口提供了2个方法Run和RunAsync。它们定义了该接口的实现类必须实现同一个处理逻辑的同步和异步方法。

为购物车提交事件编写事件处理器

有了事件处理器接口，接下来我们就可以开始为购物车提交事件添加事件处理器了。这里我们为了实现前面定义的逻辑，我们需要创建2个处理器CreateOrderHandler和ConfirmEmailSentHandler

CreateOrderHandler.cs

 public class CreateOrderHandler : IEventHandler<ShoppingCartSubmittedEvent> { private IOrderManager _orderManager = null; public CreateOrderHandler(IOrderManager orderManager) { _orderManager = orderManager; } public void Run(ShoppingCartSubmittedEvent obj) { _orderManager.CreateNewOrder(new Models.DTOs.CreateOrderDTO { Items = obj.Items.Select(p => new Models.DTOs.NewOrderItemDTO { ItemId = p.ItemId, Name = p.Name, Price = p.Price }).ToList() }); } public Task RunAsync(ShoppingCartSubmittedEvent obj) { return Task.Run(() => { Run(obj); }); } }

代码解释：
在CreateOrderHandler的构造函数中，我们注入了IOrderManager接口对象，CreateNewOrder负责最终创建订单的工作
这里为了简化代码，我直接使用了Task.Run，并在其中调用了同步方法实现

ConfirmEmailSentHandler.cs

 public class ConfirmEmailSentHandler : IEventHandler<ShoppingCartSubmittedEvent> { public void Run(ShoppingCartSubmittedEvent obj) { Console.WriteLine("Confirm Email Sent."); } public Task RunAsync(ShoppingCartSubmittedEvent obj) { return Task.Run(() => { Console.WriteLine("Confirm Email Sent."); }); } }

代码解释：
这个处理类非常简单，为了简化代码，我仅输出了一行文本来表示实际需要运行的代码。

为`OrderManager`类添加创建订单方法

IOrderManager.cs

 public interface IOrderManager { string CreateNewOrder(CreateOrderDTO dto); }

OrderManager.cs

 public class OrderManager : IOrderManager { private IOrderRepository _orderRepository; public OrderManager(IOrderRepository orderRepository) { _orderRepository = orderRepository; } public string CreateNewOrder(CreateOrderDTO dto) { var orderId = _orderRepository.CreatOrder(dto); Console.WriteLine($"One order created: {JsonConvert.SerializeObject(dto)}"); return orderId; } }

创建`EventHandlerContainer`

下面我们来编写最核心的事件处理器容器。在这里我们的事件处理器容器完成了3个功能

订阅事件(Subscribe Event)
取消订阅事件(Unsubscribe Event)
发布事件(Publish Event)

 public class EventHandlerContainer { private IServiceProvider _serviceProvider = null; private static Dictionary<string, List<Type>> _mappings = new Dictionary<string, List<Type>>(); public EventHandlerContainer(IServiceProvider serviceProvider) { _serviceProvider = serviceProvider; } public static void Subscribe<T, THandler>() where T : EventBase where THandler : IEventHandler<T> { var name = typeof(T).Name; if (!_mappings.ContainsKey(name)) { _mappings.Add(name, new List<Type> { }); } _mappings[name].Add(typeof(THandler)); } public static void Unsubscribe<T, THandler>() where T : EventBase where THandler : IEventHandler<T> { var name = typeof(T).Name; _mappings[name].Remove(typeof(THandler)); if (_mappings[name].Count == 0) { _mappings.Remove(name); } } public void Publish<T>(T o) where T : EventBase { var name = typeof(T).Name; if (_mappings.ContainsKey(name)) { foreach (var handler in _mappings[name]) { var service = (IEventHandler<T>)_serviceProvider.GetService(handler); service.Run(o); } } } public async Task PublishAsync<T>(T o) where T : EventBase { var name = typeof(T).Name; if (_mappings.ContainsKey(name)) { foreach (var handler in _mappings[name]) { var service = (IEventHandler<T>)_serviceProvider.GetService(handler); await service.RunAsync(o); } } } }

代码解释：
这里我没有直接订阅事件处理器的实例，而且订阅了事件处理器的类型
多个事件处理器可以订阅同一个事件
EventHandlerContainer的构造函数中，我们注入了一个IServiceProvider，我们可以使用它来获得对应事件处理器的实例。

在程序启动时，注册事件订阅

现在我们来Startup.cs的ConfigureServices方法，这里我们需要进行服务注册，并完成事件订阅。

 public void ConfigureServices(IServiceCollection services) { services.AddMvc().SetCompatibilityVersion(CompatibilityVersion.Version_2_2); services.AddScoped<IOrderManager, OrderManager>(); services.AddScoped<IShoppingCartManager, ShoppingCartManager>(); services.AddScoped<IShoppingCartRepository, ShoppingCartRepository>(); services.AddScoped<IOrderRepository, OrderRepository>(); services.AddScoped<IUnitOfWork, UnitOfWork>(); services.AddScoped<CreateOrderHandler>(); services.AddScoped<ConfirmEmailSentHandler>(); services.AddScoped<EventHandlerContainer>(); EventHandlerContainer.Subscribe<ShoppingCartSubmittedEvent, CreateOrderHandler>(); EventHandlerContainer.Subscribe<ShoppingCartSubmittedEvent, ConfirmEmailSentHandler>(); }

注意：这里保证一个Api请求中的所有数据库操作在一个事务里，这里我们使用Scoped作用域。这样我们就可以在调用工作单元IUnitOfWork接口的Save代码中启用事务。

最后我们来修改ShoppingCartManager, 改用发布事件的方式来完成后续创建订单和发送邮件的功能。

 public void SubmitShoppingCart(string shoppingCartId) { var shoppingCart = _unitOfWork.ShoppingCartRepository .GetShoppingCart(shoppingCartId); _unitOfWork.ShoppingCartRepository .SubmitShoppingCart(shoppingCartId); _container.Publish(new ShoppingCartSubmittedEvent() { Items = shoppingCart .Items .Select(p => new ShoppingCartSubmittedItem { ItemId = p.ItemId, Name = p.Name, Price = p.Price }) .ToList() }); _unitOfWork.Save(); }

这样ShoppingCartManager就只需要关注购物车状态的变更，而不需要关注发送确认邮件和创建订单了。

最终效果

现在让我们启动项目，

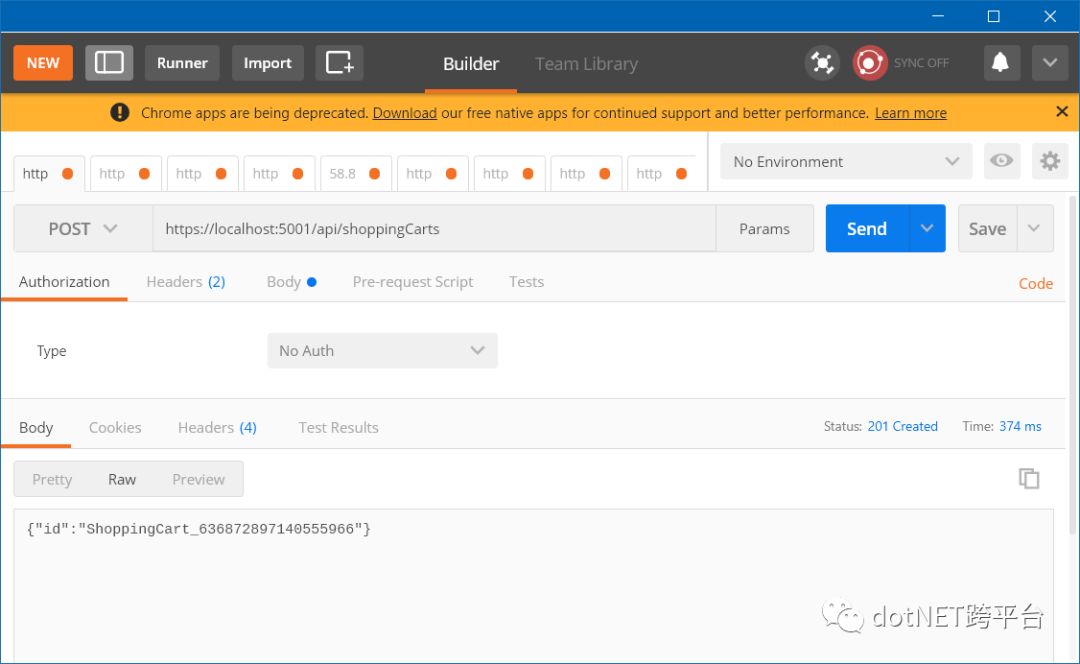
首先我们使用[POST] /api/shoppingCarts来添加一个新的购物车, 这个API会返回当前购物车的Id

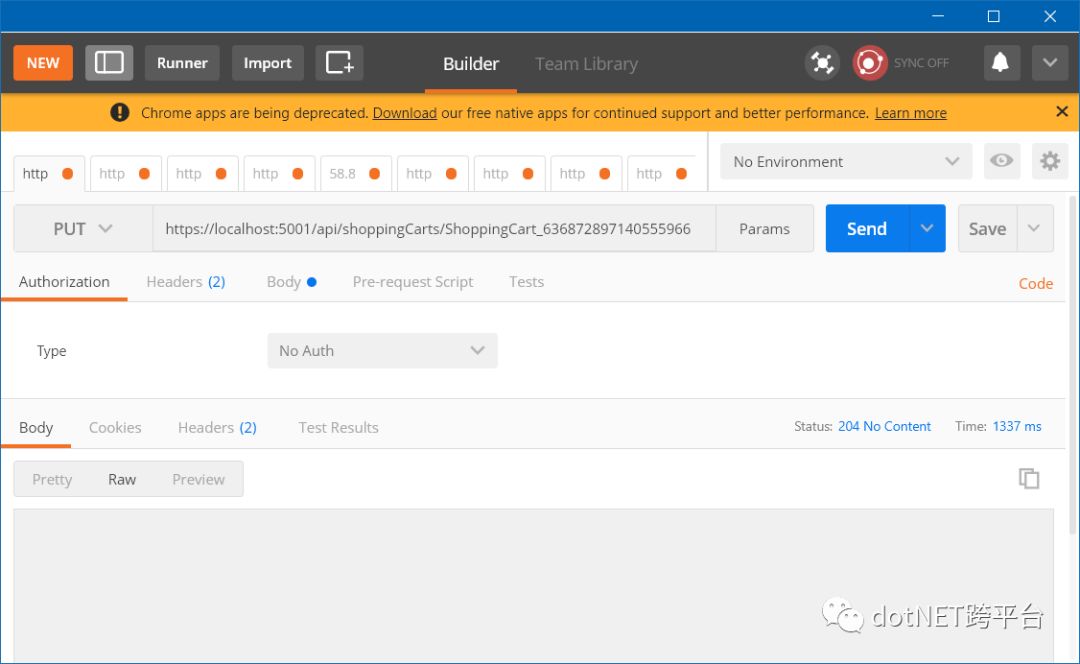
640?wx_fmt=png

然后我们使用[PUT] /api/shoppingCarts/ShoppingCart_636872897140555966来模拟提交购物车，程序返回操作成功

640?wx_fmt=png

最后我们查看一下控制台的输出日志

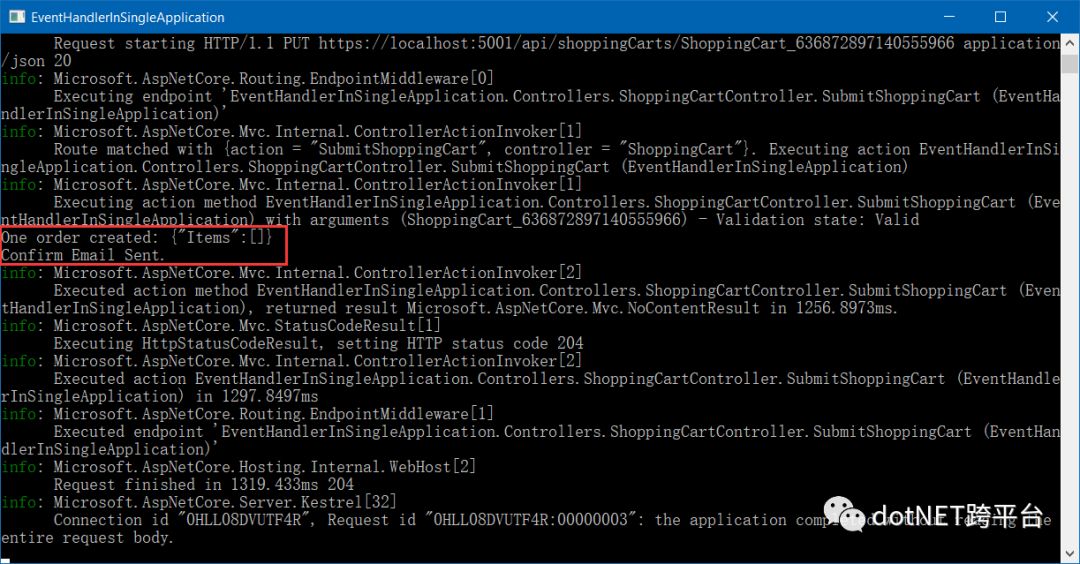
640?wx_fmt=png

2个事件处理器都被正确触发了。

总结

至此我们的代码重构完成。最终的代码中，SubmitShoppingCart方法，仅负责修改购物车状态并发布一个购物车提交的事件。生成订单和发送邮件的功能代码都被移动到了独立的处理类中。

这样的方式的好处不仅仅是完成了代码的解耦，针对后续的扩展也非常有利，想想一下，如果在未来当前项目需求追加这样一个功能，当提交购物车的时候，除了要发送确认邮件，还要发送手机短信。这时候你根本不需要去修改ShoppingCartManager类，你只需要针对ShoppingCartSubmittedEvent在再添加一个新的事件处理器即可，这也满足的SOLID的开闭原则。