static-静态

修饰属性

• 静态属性,也称为静态变量 类变量等

static 数据类型 属性名;

使用

1. 静态内容独立存放在方法区

2. 静态内容在内存中只有一份,被该类所有对象共享

   • 普通属性所有对象在对象内容中都有一份

3. 可以通过类名.静态属性名的方式直接访问静态属性

4. 静态属性封装之后,必须调用getter|setter方法才能访问

   • getter|setter是静态的:直接通过类名.getter()|setter()访问

   • getter|setter不是静态的: 必须通过任一对象名.getter()|setter()访问

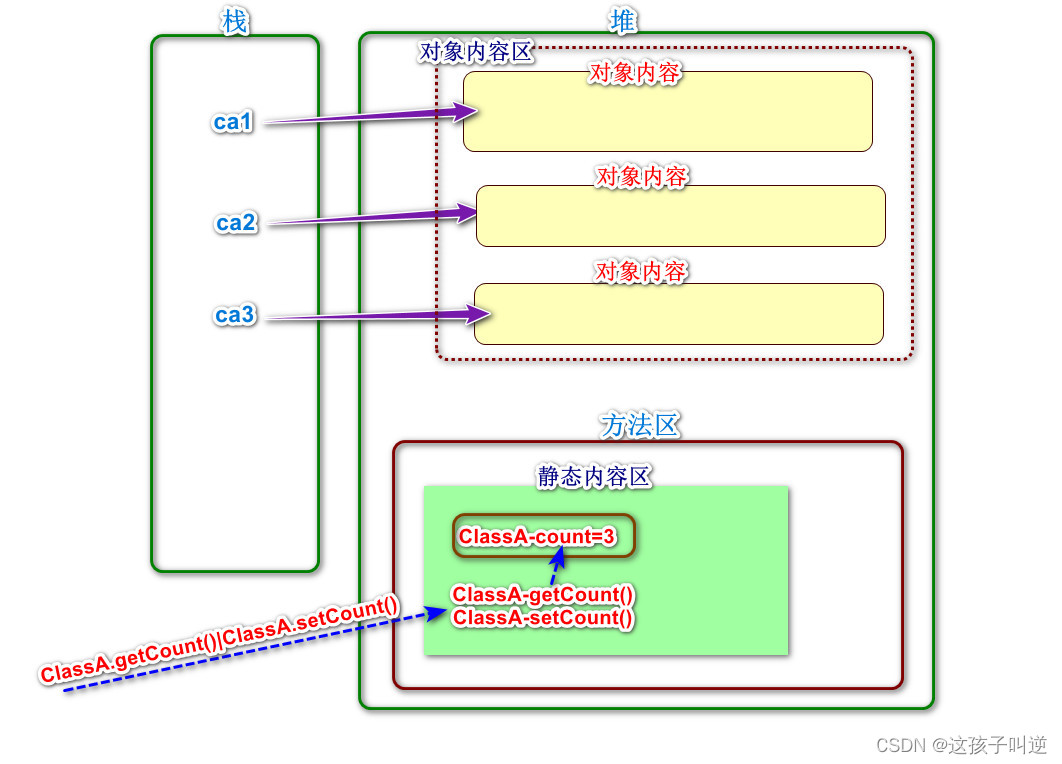
package com.by.entity;
​
public class ClassA {private static int count;//累加器属性
​public static int getCount() {return count;}
​public static void setCount(int count) {ClassA.count = count;}/* public int getCount() {return count;}
​public void setCount(int count) {ClassA.count = count;}*/
​
​public ClassA(){count++;}
}

package com.by.test;
​
import com.by.entity.ClassA;
​
public class Test2 {public static void main(String[] args) {ClassA ca1 = new ClassA();ClassA ca2 = new ClassA();ClassA ca3 = new ClassA();
​/*System.out.println(ca3.count);//3System.out.println(ca2.count);//3System.out.println(ca1.count);//3*/
​//  System.out.println(ClassA.count);//3
​System.out.println(ca1.getCount());System.out.println(ClassA.getCount());}
}

修饰方法

• 静态方法,也就是函数

访问修饰符 static 返回值类型 方法名(形参列表){//操作语句
}

使用

1. 不能访问非静态内容

   1. 什么是类加载?

      在第一次使用类内容时,通过ClassPath类路径找到对应的字节码文件,将字节码文件中的内容加载到虚拟机内存中的过程,称之为类加载, 通常只会发生一次.

   2. 触发类加载的时机

      1. 第一次创建类的对象

      2. 第一次访问静态内容时

      3. 通过Class.forName("全限定名")强制触发类加载

         • 全限定名:类的完整路径,也就是包名.类名

      4. 子类类加载也会触发父类的类加载

      5. 只声明引用不会触发类加载

   静态内容是在类加载时进入内存,但是非静态内容是在创建对象时进入内存

   非静态方法可以访问任何内容

2. 无法使用this和super关键字

   • 使用静态内容时对象可能并未创建

3. static无法修饰局部变量

   • 局部变量的作用范围使其无法成为类变量

4. 无法修饰构造

   • 构造无法通过类名直接调用

5. 子类可以继承和重写父类静态方法,但是在多态的前提下,仍然执行父类内容

   • 静态内容的执行关注的是引用类型

修饰初始代码块-了解

初始代码块

{//初始代码块
}

使用

1. 通常写在属性之下,构造之上

2. 作用为构造方法共有内容的提炼,通常用于给属性赋值

3. 在创建对象时执行,先执行初始代码块再执行构造内容,可以执行多次

static修饰初始代码块

static{//静态初始代码块
}

使用

1. 内部内容的限制与静态方法相同

2. 在类加载的时候执行,通常只会执行一次

3. 作用为给静态属性赋值