这里是Z哥的个人公众号

每周五早8点 按时送达

当然了，也会时不时加个餐～

我的第「77」篇原创敬上

在一个分布式系统的开发团队中，有一些问题是很容易产生程序员之间矛盾的。

其中之一就是「业务归属」，就是当新加/修改一个业务的时候，代码变更应该放到你负责的系统还是我负责的系统里？

一些业务轮廓很清晰的就不用说了，大家的认定都是一样的。比如商品相关的放到商品服务，会员相关的放到会员服务。

但是对于轮廓模糊的业务，大家作出的决定就不一定相同了。

这个时候起决定性作用的并不是各自的工作经验，而是你的「业务思维」是否具有全局性，以及对全局业务的了解程度如何。

一旦草率的作出了“不合适”的归属划定，后续将会带来大量的额外成本，协作、更高的bug率等等。

看看以下的场景是不是平时有见到过？

• 嗨，小明，我这里有个bug需要你和我一起调试下。

• 当初如果这个业务在这里就好了，现在已经积重难返了，只能推倒重做了。

• 我觉得这个问题可能是这里导致的，也有可能是那里导致的。

所以，一个业务归属于哪个项目，看似是一个很简单的选择题。但是每个人心中的默认选择是不同的，比如以下两种截然不同的倾向。

• 我能解决的就我解决咯，实在解决不了的再给对方

• 只能我这里解决的就我这里解决，其它的全部对方来

其实这些选择都是因人而异的，很难形成一个放之四海而皆准的共识。

如果双方都选择第二点，产生冲突、争执是必然的。

哪怕大家都选择“为他人着想“的第一点，只是避免了相互扯皮，但还是无法避免后续业务边界混乱付出的额外成本。

所以，我们还是需要从中提炼出本质的东西作为决策的准则。

Z哥我认为思考业务归属的时候，本质上还是逃不开「高内聚低耦合」范围，一个合理的项目归属认定，会让软件系统离每个人所期望的「高内聚低耦合」更近一步。

因为「业务归属」和「高内聚低耦合」一样，都在“划线”，明确边界。

但是我们很多时候其实并不知道“线”应该具体画在什么位置，只是知道一个大概方位而已。

其实，如果当我们的系统只是一个单体应用的话，是不存在「业务归属」问题的。

因此它是在分工协作下所产生的一个副作用。

但是，只要我们继续保持分工协作来开发一个分布式系统，这个问题就是绕不开的一道坎。

在工作中，由于边界不清容易产生业务归属分歧的场景主要是以下两点。

• 一个新业务，需要两边配合完成

• 一个老业务，一部分在A处理，一部分在B处理。

这里先停顿一分钟，想一想，如果是你的话，该如何来作出选择？

Z哥我给你的建议是，你可以这样来考虑：哪边缺了这个业务的话，会导致至少一个流程走不通。

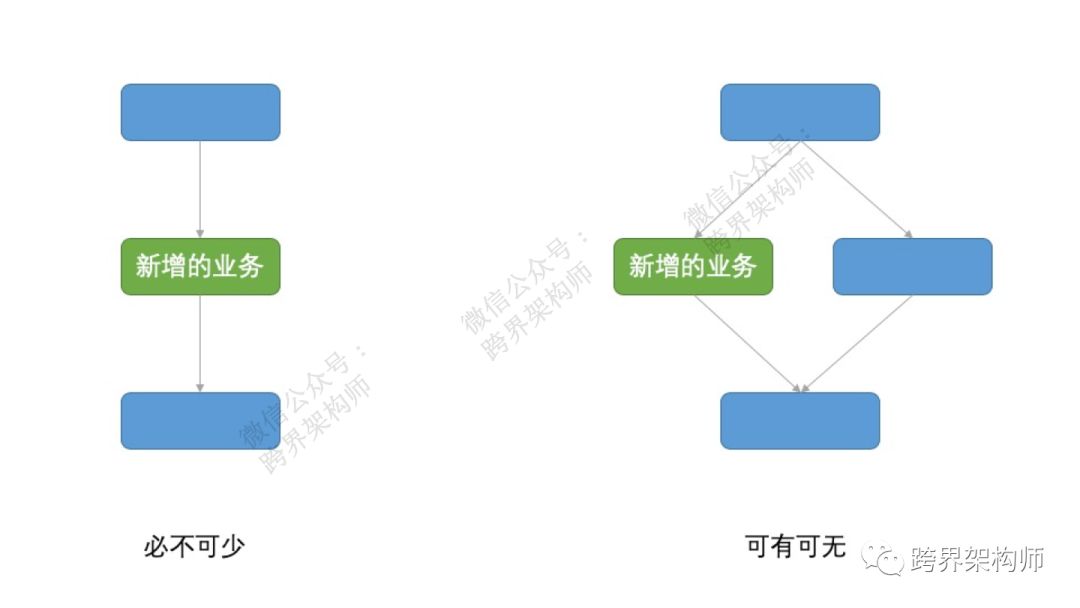
来举两个例子帮助你理解。

一个电商网站现在要上线一个会员卡的功能，类似阿里的88会员这种。 

效果是买了这个会员卡的用户，在该平台购买自营商品时，享受8折优惠。

那么你来思考一下？这个业务到底是放到「会员服务」还是「促销服务」？

参照上面的建议来思考就是回答两个问题：

• 会员服务缺少了这个会员卡业务，是否有至少一个流程走不通？

• 促销服务缺少了这个会员卡业务，是否有至少一个流程走不通？

很显然，会员卡虽然有一个打折功能，但是这个打折是建立在一个身份标识上的。

那么就要思考一下，这个身份标识后续是否会在整个购物链路中的多个环节有露出展示或者对应的专属业务，比如专属客服、每月领福利等等。

另外你会发现，如果促销想实现打8折的效果，可以完全不需要有会员卡的存在也能做到。

所以，这个会员卡本质更像是会员属性的一个扩展，是跟着某个具体的会员走的。

假如最终不小心被归属到了促销服务，则每次围绕会员卡展开的业务都需要与促销服务产生耦合才能完成，很明显就背离了「高内聚低耦合」的初衷。

所以，对促销服务来说，会员卡业务并不是必不可少的。相对来说，会员服务与它的关系更紧密。

至此，第一个例子的答案就出来了，应该放到会员服务。

再来看第二个例子。

随着社交电商模式的崛起，该电商平台想上一个拼团功能。

那么这个功能该放到「购物车服务」里？还是「促销服务」里呢？

同样回答两个问题：

• 购物车服务缺少了这个拼团业务，是否有至少一个流程走不通？

• 促销服务缺少了这个拼团业务，是否有至少一个流程走不通？

首先，大家最容易想到的是，拼团一般都是直接下单，不经过购物车，自然不用放到购物车服务，放到促销服务才是合适的。

这个理解完全合理。但是我们可以再想一下，拼团就必须要放到促销服务里吗？

拼团其实也就是一口价，也不用经过促销的价格计算。

如此看来，拼团对促销来说也不是“刚需”。

这个时候将拼团服务独立出来才是更好的选择。因为在这个例子里，缺少拼团业务，对两个服务都不会产生流程上的阻碍。

反而独立出来后，后续对拼团业务的调整，会更容易进行。不用对购物车服务、促销服务产生任何影响。

至此，我相信你对如何判断一个业务的项目归属已经有感觉了。如果你想贯彻「高内聚低耦合」作为系统的设计方针，不妨学习一下「领域驱动设计」。

这是由Eric Evans提出的概念，将建模作为、划分系统边界等等作为最高优先级的开发模式。

我相信，随着未来的业务越来越复杂，基于业务作为出发点考虑的软件设计理念会越来越凸显价值。

因为技术只是实现业务的介质之一，况且新技术的产生速度正在越来越快。

那么，与其用最好新技术，不如替业务选择最适合的技术。

好了，我们总结一下。

这次Z哥先帮你分析了一下产生「业务归属」分歧背后的原因。

然后，再分享了一个正确思考这个问题的建议，还举了两个例子。

以后再遇到拿捏不准业务该归属到哪个项目的话。只要记住一句话：哪边缺了这个业务，会有至少一个流程走不通。如果都能通，那么这个新业务就适合“独立门户”。

在程序员们的日常工作中，容易发生分歧的问题还有很多，不过，其实大部分问题都有一个通解——全局的业务思维。

推荐阅读：

• 分布式系统关注点——缓存背后的“毁灭种子”

• 8个月打磨，一份送给程序员的「分布式系统」合集

原创不易，如果你觉得这篇文章还不错，就「在看」或者「分享」一下吧。鼓励我的创作 ：）

如果有希望我写一下什么主题的话，欢迎在后台给我留言哦～